Abstract
In today's dynamic construction landscape, where challenges like complexity, costs, and uncertainties loom large, the selection of consultants emerges as a pivotal factor for project triumph. Among the array of methods available, Quality and Cost Based Selection (QCBS) stands out for its holistic approach, considering both technical prowess and financial considerations. Yet, amidst its structured framework, the evaluation of technical proposals within QCBS often grapples with subjectivity, despite the presence of well-defined criteria. This study boldly tackles this challenge head-on by delineating common criteria and sub-criteria for consultant selection within the esteemed Department of Water Resources and Irrigation (DWRI). Leveraging the innovative Fuzzy Analytic Hierarchy Process (AHP), our endeavor is to ascertain the relative significance of these criteria and sub-criteria. Through the fusion of Fuzzy AHP and Fuzzy Techniques for Order Preference by Similarity to Ideal Solution (TOPSIS), our study aspires to revolutionize consultant ranking methodologies. The ingenious application of Fuzzy AHP empowers us to derive independent weights for criteria and sub-criteria, thereby embracing the inherent ambiguity and nuances of qualitative factors. Subsequently, employing Fuzzy TOPSIS, we aim to systematically rank consultant alternatives based on their Closeness Coefficients, heralding a paradigm shift in evaluation paradigms. Through this groundbreaking hybrid approach, our study endeavors to elevate the consultant selection process, ensuring an impeccable alignment of chosen consultants with project requisites and benchmarks. By dispelling the shadows of subjective decision-making uncertainties, our research holds the promise of ushering in a new era of excellence in the realm of construction projects under the aegis of the Department of Water Resources and Irrigation.
Highlights
- Developed a hybrid Fuzzy AHP-TOPSIS model for DWRI consultant selection.
- Determined criteria weights and ranked consultants systematically.
- Comparative analysis shows consistency with traditional methods.
- Reduced subjectivity and enhanced transparency in decision-making.
1. Introduction
In today's fiercely competitive landscape, the task of selecting the perfect consultant for construction projects is both intricate and pivotal. It involves a myriad of criteria, encompassing both qualitative and quantitative aspects, crucial for ensuring not just the success of individual projects but the prosperity of the entire organization. However, amidst the decision-making process lie challenges of fuzziness, imprecision, vagueness, and incompleteness, making the selection of a qualified consultant a daunting task for project owners. This multi-criteria decision problem heavily relies on subjective assessments by decision-makers, compounded by the inherent ambiguity and uncertainty prevalent in construction projects [1]. While technical and financial evaluation criteria are outlined, the evaluation process often lacks objectivity, with criteria weights presented as ranges rather than precise values. This ambiguity extends to the selection of consultants, where criteria weights are provided within ranges while the definition of sub-criteria and their respective weights remains undefined. Consequently, the Department of Water Resources and Irrigation (DWRI) faces the challenge of tailoring sub-criteria to meet their specific project needs [2]. Such ambiguity raises concerns regarding the relevance and appropriateness of criteria and their weights, potentially resulting in the selection of unqualified consultants. The repercussions of such selections can manifest as poor service quality, inaccurate cost estimates, exclusion of qualified consultants, increased costs, and strained client-consultant relationships. To tackle these challenges and infuse objectivity into the consultant selection process, a methodology integrating the Fuzzy Analytic Hierarchy Process (FAHP) and Fuzzy Techniques for Order Preference by Similarity to Ideal Solution (FTOPSIS) is proposed. This approach aims to establish precise weights for criteria and sub-criteria, thereby facilitating more accurate and informed decision-making [3]. By leveraging linguistic ratings and interval judgments, the methodology endeavors to align with the inherent subjectivity in evaluating technical proposals within a defined range of percentages.
2. Literature review
Consultant selection poses a multi-criteria decision problem primarily influenced by the inherent uncertainty and ambiguity prevalent in construction projects, alongside the subjective judgments of decision makers. Various Multi-Criteria Decision Making (MCDM) models such as AHP, PROMETHEE, ELECTRE, TOPSIS, and VIKOR exist, each with its unique algorithm. Among these, the AHP technique stands out, widely adopted in MCDM and other problem-solving contexts with remarkable success [4]. Renowned for its efficacy, the AHP method offers a valuable decision-making tool for tackling and dissecting complex problems. By breaking down intricate problems into simpler components, the AHP method provides a structured approach to problem-solving [5]. The criteria weights were determined by fuzzy AHP in the initial phase of the proposed approach, and the alternatives were ordered using TOPSIS in the final phase.
2.1. Triangular fuzzy number (TFN)
Uncertain and vague data in decision-making problems can be effectively addressed through the application of the Fuzzy Set Theory, pioneered by Zadeh (1965) [17]. A fuzzy set comprises membership functions that encapsulate degrees of membership using real numbers within the [0, 1] interval. Membership values of zero and one signify absence and full membership, respectively. Values between zero and one denote varying degrees of membership. Additionally, translating linguistic terms into fuzzy numbers presents a promising approach to mitigate vagueness and ambiguities. Among the diverse shapes of fuzzy numbers, the triangular fuzzy number stands out as the most prevalent and simplest form. Comprising triplets (L, M, U), where L represents the minimum likely value, M denotes the probable value, and U signifies the maximum possible value, it offers a structured representation of fuzzy events.
2.2. Fuzzy analytic hierarchy process (FAHP)
The Analytic Hierarchy Process (AHP) method, introduced by Satty [18], is a quantitative technique utilized for multi-criteria decision making, initially proposed by Satty [19]. An extension of this conventional approach is the Fuzzy Analytic Hierarchy Process (FAHP), which serves as a decision-making tool tailored for analyzing complex problems featuring multiple criteria and alternatives. While the conventional AHP method has its merits, it may not wholly capture the nuances of human decision-making, as decision-makers often prefer to provide interval judgments rather than singular numeric values [3]. Fuzzy AHP addresses this constraint by enabling decision-makers to articulate their judgments using linguistic terms alongside corresponding fuzzy numbers, such as “equal importance (1, 1, 1)”, “moderate importance (2, 3, 4)”, “strong importance (4, 5, 6)”, “very strong importance (6, 7, 8)”, or “extreme importance (9, 9, 9)”. Pairwise comparisons within fuzzy AHP are conducted using fuzzy numbers, with aggregation performed through fuzzy arithmetic. This framework accommodates uncertainty and vagueness in decision-making processes, rendering fuzzy AHP particularly advantageous in scenarios where precise numerical data may be scarce or challenging to obtain.
Table 1Summary of studies in consultant/personnel/contractor selection
References | Topic | Method | Objectives |
C.-A. Tsai, S. W. Lo and T.-M. Lin [6] | An Analytical Framework with Sensitivity Analysis to Quantify Management Consultancy Selection | AHP | To quantify the priority of criteria and sub-criteria in management consultancy selection |
R. Karki [2] | A Study of Criteria for Selection of Consultant in Nepal | AHP | To determine the criteria and sub-criteria for selection of consultant that need to be considered by the public entity |
F. K. T. K. Cheung, Judy Leung FungSkitmore, Martin [7] | Multi-criteria evaluation model for the selection of architectural consultants | AHP | To identify the criteria (and sub-criteria) for architectural consultants’ selection in Hong Kong |
A. Kazaz, M. T. B., H. K., T. A., B. and Er [8] | Evaluation of Consulting Firms Selection in Construction Projects by Using Fuzzy Logic | Fuzzy Model | To determine the prioritized criterions in the selection process |
M. K. Trivedi, M. K. Pandey and S. S. Bhadoria [3] | Prequalification of Construction Contractor using a FAHP | Fuzzy AHP | To develop a fuzzy analytical hierarchy approach to rank the suitable contractor for the housing project |
L. L. H. a. Y. D. L. Tran Thanh Ha [9] | A Fuzzy AHP Model for Selection of Consultant Contractor in Bidding Phase in Vietnam | Fuzzy AHP | To identify the criteria (and sub-criteria) for PMC’s selection in Vietnam |
A. Nieto-Morote, F. Ruz-Vila [10] | A fuzzy multi-criteria decision-making model for construction contractor prequalification | Fuzzy AHP/TOPSIS | To evaluate the contractor prequalification based on identified selection criteria. |
José Ramón San Cristóbal [11] | Contractor Selection Using Multicriteria Decision-Making Methods | Fuzzy AHP/TOPSIS | To rank the contractor based on identified selection criteria |
Mehtap Dursun, E. Ertugrul Karsak [12] | A fuzzy MCDM approach for personnel selection | Fuzzy AHP/TOPSIS | To develop a decision-making approach to a multiple information sources problem for the personnel selection |
A. Kelemenis, K. Ergazakis and D. Askounis [13] | Support managers’ selection using an extension of fuzzy TOPSIS | Fuzzy AHP/TOPSIS | To support adequately the decision on managers’ selection within organizations |
A. M. Kelemenis and D. T. Askounis [14] | An extension of fuzzy TOPSIS for personnel selection | Fuzzy AHP/TOPSIS | To support adequately the decision on project team member selection. |
C.-N. Liao [15] | An Evaluation Model Using Fuzzy TOPSIS and Goal Programming for TQM Consultant Selection | Fuzzy AHP/TOPSIS | To analyze the TQM consultants using different criteria weights |
M. Saremi, S. F. Mousavi and A. Sanayei [16] | TQM consultant selection in SMEs with TOPSIS under fuzzy environment | Fuzzy AHP/TOPSIS | To propose a methodology based on fuzzy TOPSIS for the external consultant selection problem |
2.3. Fuzzy technique for order preference by similarity to ideal solution (FTOPSIS)
TOPSIS, a Multi-Criteria Decision Making (MCDM) method pioneered by Hwang and Yoon [20]; stands out as a robust framework for decision-making processes. When TOPSIS integrates fuzzy numbers to capture uncertain or imprecise information, it morphs into a fuzzy technique. Fuzzy TOPSIS extends the classical TOPSIS method by embracing linguistic terms or fuzzy numbers to represent weights, criteria, or performance scores. This augmentation empowers decision-makers to adeptly navigate subjective judgments and uncertainties. TOPSIS introduces an index termed “similarity to the positive-ideal solution (PIS)” and “remoteness from the negative-ideal solution (NIS)”. Leveraging these indices, the method identifies an alternative with the maximum similarity to the ideal solution.
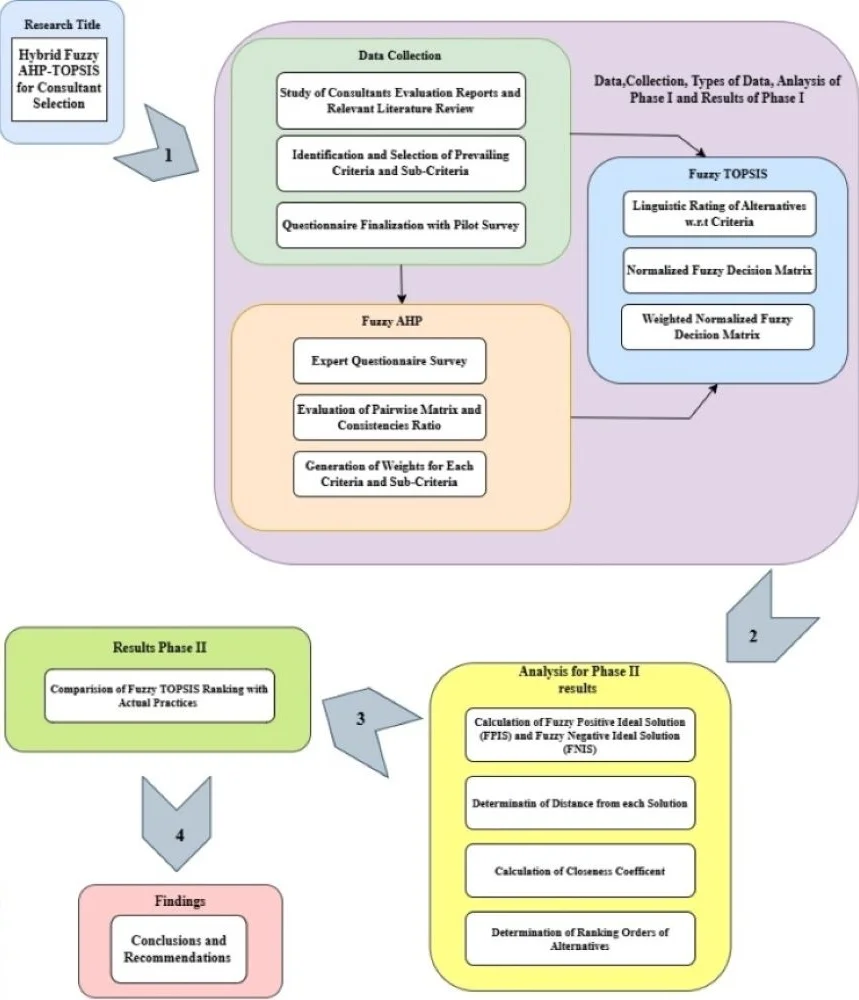
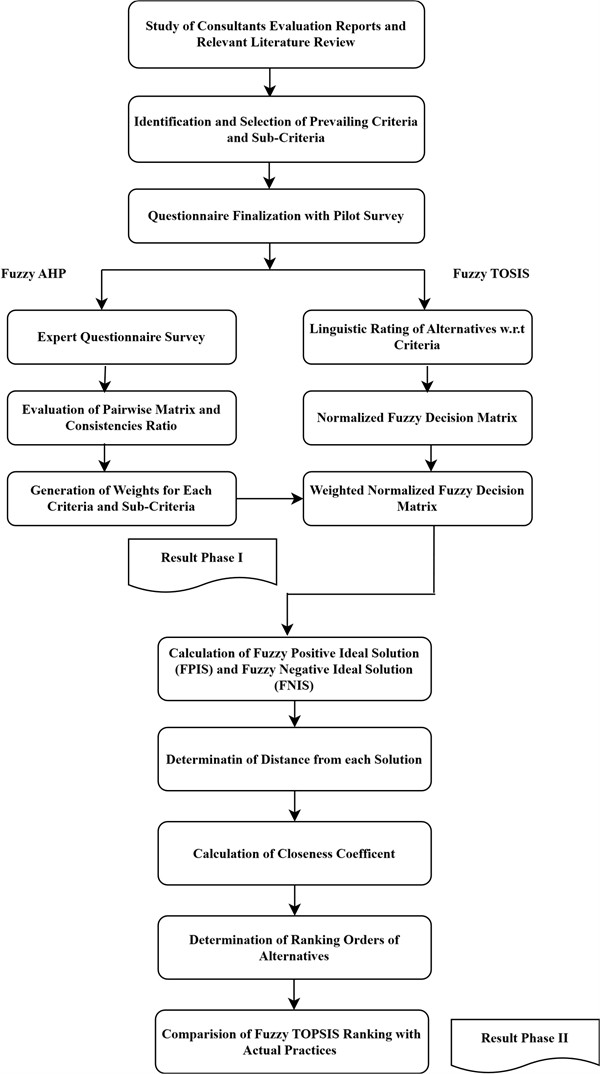
Fig. 1Hybrid approach framework
2.4. Proposed hybrid fuzzy AHP- fuzzy TOPSIS approach
As shown in framework (Fig. 1), a review of the literature was conducted in order to specify the criteria and sub-criteria for the selection of consultants in DWRI. The weightage of each criteria and sub-criteria was defined using MCDA tool Fuzzy AHP method. The Questionnaire was prepared for expert survey through which weightage was computed. Linguistic Rating of alternatives w.r.t criteria was done for ranking of criteria by Fuzzy TOPSIS method. The study data in the form of qualitative was transformed into quantitative data followed by fuzzy AHP and fuzzy TOPSIS method.
3. Data collection
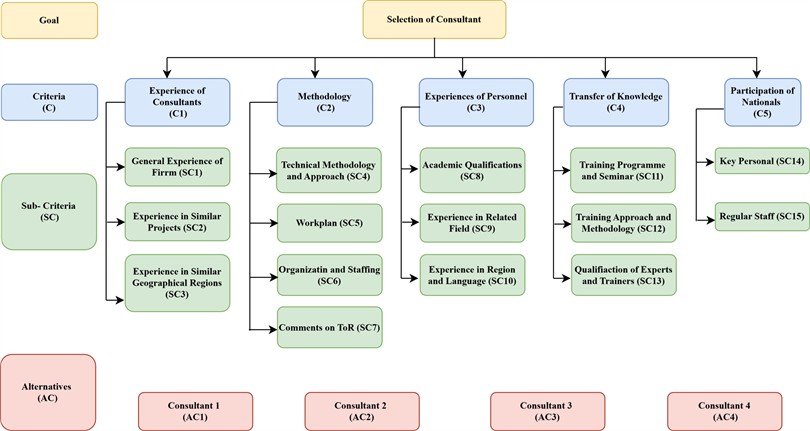
The available literature on consultant’s selection methods were broadly searched and studied to identify the major selection criteria and respective sub-criteria in alignment to resemble the practices in DWRI. Questionnaire was prepared on the basis of Saaty’s 9-point scale for pairwise comparison of criteria and sub-criteria as per hierarchical model as shown in Fig. 2. Pretesting of questionnaire was done among two respondents and finalized questionnaire form was distributed to Twenty- Eight respondents i.e., consultant evaluation committee members / Consultants of different projects of Department of Water Resources and Irrigation. For Fuzzy TOPSIS, the rating sheet were provided to same member of the evaluation consultant committee with proper briefing of scale and linguistic rating to be filled.
Fig. 2Hierarchical model of consultant selection
4. Results
4.1. Fuzzy AHP results
Pair-wise comparison matrices obtained from the respondents were combined using the geometric mean approach at each hierarchy level to obtain the corresponding consensus pair-wise comparison matrices. Each of these matrices were then translated into the corresponding largest eigen value problem and were solved to find the normalized and unique priority weights for each criterion. All the experts’ ratings were categorized and pairwise comparison matrices were made. Their Consistency Index and Consistency Ratios were calculated and checked.
Each of the criteria and sub-criteria under main criteria were subjected to confirm the consistent by the consistency ratio less than 0.1 obtained from 28 experts. Then, the weightage was aggregated and turned into fuzzy weights as proposed by (Buckley, 1985) [21]. The local weightages for sub-criteria under main criteria were obtained as the result from the aggregated data calculation. The average global weights of all criteria calculated from experts’ rating are presented below in Table 2. So, in this section the above frequency of consistent data was subjected to aggregated fuzzified pair-wise comparison matrix followed by defuzzification, normalization and following result were obtained: the weightage of the main criteria and local and global weightage of sub-criteria under each criterion.
Table 2Local and global weightage of criteria and sub-criteria
Goal | Criteria | Sub-criteria | Local weights | Global weights |
Selection of Consultant | Experience of consultant (C1) | 0.2958 | 0.2958 | |
Methodology (C2) | 0.2087 | 0.2087 | ||
Qualification of key personnel (C3) | 0.3134 | 0.3134 | ||
Transfer of knowledge (C4) | 0.0921 | 0.0921 | ||
Participation of nationals (C5) | 0.0899 | 0.0899 | ||
Experience of consultant (C1) | 0.2958 | 0.2958 | ||
General experience of firm (SC1) | 0.1113 | 0.0329 | ||
Experience in similar projects (SC2) | 0.5604 | 0.1657 | ||
Experience in similar geographical area (SC3) | 0.3282 | 0.097 | ||
Methodology (C2) | 0.2087 | 0.2087 | ||
Technical approach and methodology (SC4) | 0.4225 | 0.0881 | ||
Work plan (SC5) | 0.2826 | 0.0589 | ||
Organization and staffing (SC6) | 0.1805 | 0.0376 | ||
Comments on ToR (SC7) | 0.1142 | 0.0238 | ||
Qualification of key personnel (C3) | 0.3134 | 0.3134 | ||
Academic qualification (SC8) | 0.1684 | 0.0527 | ||
Experience in related field (SC9) | 0.6117 | 0.1917 | ||
Experience in region and language (SC10) | 0.2198 | 0.0688 | ||
Transfer of knowledge (C4) | 0.0921 | 0.0921 | ||
Training program and seminar (SC11) | 0.2301 | 0.0211 | ||
Training approach and methodology (SC12) | 0.3402 | 0.0313 | ||
Qualification of experts and trainers (SC13) | 0.4295 | 0.0395 | ||
Participation of nationals (C5) | 0.0899 | 0.0899 | ||
Key Personnel (SC14) | 0.7636 | 0.0686 | ||
Regular Staff (SC15) | 0.2363 | 0.0212 |
From Table 2, it was observed that the five highest weighted sub-criteria for standing list were: experience in related field, experience in similar projects, experience in similar geographical area, Technical Approach and Methodology and experience in region and language; whereas the five lowest weighted sub-criteria were: organization and staffing, general experience of firm, Training approach and methodology, comments on TOR, training program and seminar, and regular staff.
4.1.1. Sample calculation for Fuzzy AHP
Buckley’s method of calculation for main criteria only.
The fuzzified pairwise comparison matrix was aggregated by the geometric means to obtain the aggregated fuzzified pairwise comparison matrix () as shown in Table 3.
The row operation for matrix of above Table 3 was conducted to obtain the Fuzzy Geometric Mean Value for all criteria as tabulated in Table 4.
For experience of consultant (C1):
(1*8/7*4/7*2*13/6) (1/5), (1*2*5/6*3*16/5) (1/5), (1*3*5/4*4*17/4) (1/5) = (1.2335, 1.7438, 2.2776).
The Fuzzy weights can be calculated as follows and tabulated in Table 5.
(1.2335, 1.7438, 2.2776) * (0.129, 0.172, 0.2382) = (0.1592, 0.3001, 0.5426).
Table 3Aggregated fuzzified pairwise comparison matrix for criteria
Criteria | C1 | C2 | C3 | C4 | C5 |
C1 | (1, 1, 1) | (8/7, 2, 3) | (4/7, 5/6, 5/4) | (2, 3, 4) | (13/6, 16/5, 17/4) |
C2 | (1/3, 1/2, 7/8) | (1, 1, 1) | (2/5, 4/7, 7/8) | (2, 3, 4) | (17/9, 20/7, 21/8) |
C3 | (3/4, 6/5, 7/4) | (8/7, 12/7, 22/9) | (1, 1, 1) | (19/8, 7/2, 9/2) | (2, 3, 4) |
C4 | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (2/9, 2/7, 3/7) | (1, 1, 1) | (2/3, 8/7, 11/6) |
C5 | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (5/9, 7/8, 3/2) | (1, 1, 1) |
Table 4Fuzzy geometric mean value for criteria
Criteria | l | m | u |
Experience of consultant (C1) | 1.2335 | 1.7438 | 2.2776 |
Methodology (C2) | 0.8725 | 1.1901 | 1.635 |
Qualification of key personnel (C3) | 1.3149 | 1.8583 | 2.401 |
Transfer of knowledge (C4) | 0.3946 | 0.5187 | 0.7221 |
Participation of nationals (C5) | 0.3819 | 0.4998 | 0.7107 |
Sum | 4.1974 | 5.8107 | 7.7464 |
Inverse | 0.129 | 0.172 | 0.2382 |
Table 5Fuzzy weights for criteria
Criteria | l | m | u |
Experience of consultant (C1) | 0.1592 | 0.3001 | 0.5426 |
Methodology (C2) | 0.1126 | 0.2048 | 0.3895 |
Qualification of key personnel (C3) | 0.1697 | 0.3198 | 0.572 |
Transfer of knowledge (C4) | 0.0509 | 0.0892 | 0.172 |
Participation of nationals (C5) | 0.0493 | 0.086 | 0.1693 |
Table 6Defuzzified and normalized Weights for criteria
Criteria | Defuzzified weight (Mi) | Normalized weight (Ni) |
Experience of consultant (C1) | 0.3339 | 0.2958 |
Methodology (C2) | 0.2356 | 0.2087 |
Qualification of key personnel (C3) | 0.3538 | 0.3134 |
Transfer of knowledge (C4) | 0.104 | 0.0921 |
Participation of nationals (C5) | 0.1015 | 0.0899 |
Sum | 1.1288 | 1 |
The defuzzification and normalization of the fuzzy weights can be conducted as follows and tabulated in Table 6. (0.1592+0.3001+0.5426)/3 = 0.3339, 0.3339/1.1288 = 0.2958.
Similarly, normalized local weights for all sub-criteria under main criteria were calculated. After this, these weights were multiplied with the weight of main Criteria to obtain Average Global Weights as shown in Table 2. Finally, the obtained average weights were taken for Fuzzy TOPSIS for further calculation.
4.2. Fuzzy TOPSIS results
Here, the model practiced in DWRI representing a national RFP, comprising four main criteria (C1, C2, C3, C4), involving four consultants: Consultant 1 (AC-1), Consultant 2 (AC-2), Consultant 3 (AC-3), and Consultant4 (AC-4) was shortlisted for the study based on the varying nature of work and the level of competition. Samples of consultant evaluations were organized, and linguistic ratings for the alternatives were collected from the same three members of the consultant evaluation committee as Decision Makers (DM) by briefing them on expected output as shown in Table 7.
Table 7Linguistic rating of alternatives w.r.t. criteria by three DM’S
Decision Maker-1 | ||||
Consultant | Experience of consultant (C1) | Methodology (C2) | Qualification of key personnel (C3) | Transfer of knowledge (C4) |
AC-1 | Medium good (MG) | Good (G) | Good (G) | Medium good (MG) |
AC-2 | Very good (VG) | Good (G) | Medium good (MG) | Good (G) |
AC-3 | Very good (VG) | Fair (F) | Good (G) | Fair (F) |
AC-4 | Good (G) | Medium good (MG) | Good (G) | Very poor (VP) |
Decision Maker-2 | ||||
Consultant | Experience of consultant (C1) | Methodology (C2) | Qualification of key personnel (C3) | Transfer of knowledge (C4) |
AC-1 | Medium good (MG) | Good (G) | Good (G) | Good (G) |
AC-2 | Very good (VG) | Good (G) | Medium Good (MG) | Very good (VG) |
AC-3 | Very good (VG) | Fair (F) | Good (G) | Fair (F) |
AC-4 | Good (G) | Medium Good (MG) | Good (G) | Very poor (VP) |
Decision Maker-3 | ||||
Consultant | Experience of consultant (C1) | Methodology (C2) | Qualification of key personnel (C3) | Transfer of knowledge (C4) |
AC-1 | Medium good (MG) | Good (G) | Good (G) | Good (G) |
AC-2 | Very good (VG) | Good (G) | Medium good (MG) | Very good (VG) |
AC-3 | Very good (VG) | Fair (F) | Good (G) | Medium good (MG) |
AC-4 | Good (G) | Medium good (MG) | Good (G) | Very poor (VP) |
These ratings were combined into a seven-point scale using respective triangular fuzzy numbers and represented in Table 8.
Table 8Fuzzy decision matrix
Decision Maker-1 | ||||||||||||
Consultant | Experience of consultant (C1) | Methodology (C2) | Qualification of key personnel (C3) | Transfer of knowledge (C4) | ||||||||
AC-1 | 5 | 7 | 9 | 5 | 7 | 9 | 7 | 9 | 10 | 7 | 9 | 10 |
AC-2 | 9 | 9 | 10 | 7 | 9 | 10 | 5 | 7 | 9 | 7 | 9 | 10 |
AC-3 | 9 | 9 | 10 | 3 | 5 | 7 | 7 | 9 | 10 | 3 | 5 | 7 |
AC-4 | 7 | 9 | 10 | 0 | 1 | 1 | 7 | 9 | 10 | 5 | 7 | 9 |
Decision Maker-2 | ||||||||||||
Consultant | Experience of consultant (C1) | Methodology (C2) | Qualification of key personnel (C3) | Transfer of knowledge (C4) | ||||||||
AC-1 | 5 | 7 | 9 | 7 | 9 | 10 | 7 | 9 | 10 | 7 | 9 | 10 |
AC-2 | 9 | 9 | 10 | 9 | 9 | 10 | 5 | 7 | 9 | 7 | 9 | 10 |
AC-3 | 9 | 9 | 10 | 3 | 5 | 7 | 7 | 9 | 10 | 3 | 5 | 7 |
AC-4 | 7 | 9 | 10 | 0 | 1 | 1 | 7 | 9 | 10 | 5 | 7 | 9 |
Decision Maker-3 | ||||||||||||
Consultant | Experience of consultant (C1) | Methodology (C2) | Qualification of key personnel (C3) | Transfer of knowledge (C4) | ||||||||
AC-1 | 5 | 7 | 9 | 7 | 9 | 10 | 7 | 9 | 10 | 7 | 9 | 10 |
AC-2 | 9 | 9 | 10 | 9 | 9 | 10 | 5 | 7 | 9 | 7 | 9 | 10 |
AC-3 | 9 | 9 | 10 | 5 | 7 | 9 | 7 | 9 | 10 | 3 | 5 | 7 |
AC-4 | 7 | 9 | 10 | 0 | 1 | 1 | 7 | 9 | 10 | 5 | 7 | 9 |
The criteria were categorized into Benefit Function (where larger values are preferable) for all alternatives neglecting the Cost Function. Then, the combined and normalized fuzzy decision matrix was shown in Table 9 and Table 10 respectively.
These normalized matrices were multiplied by the average weights of all criteria obtained from fuzzy AHP to generate a Weighted Normalized Fuzzy Decision Matrix as in Table 11. To calculate the Closeness Coefficient, the FPIS (Fuzzy Positive Ideal Solution) and FNIS (Fuzzy Negative Ideal Solution) were determined. FPIS represents the maximum value among all alternatives, while FNIS represents the minimum value.
Distance () and sum of distance () from FPIS & Distance () and sum of distance () from FNIS were calculated and presented in Table 13 and 14 respectively.
Finally, the alternatives were ranked based on their closeness coefficient as shown in Table 14.
Table 9Combined fuzzy decision matrix (X~)
Consultant | Experience of consultant (C1) | Methodology (C2) | Qualification of key personnel (C3) | Transfer of knowledge (C4) | ||||||||
AC-1 | 5 | 7 | 9 | 5 | 8.33 | 10 | 7 | 9 | 10 | 7 | 9 | 10 |
AC-2 | 9 | 9 | 10 | 7 | 9 | 10 | 5 | 7 | 9 | 7 | 9 | 10 |
AC-3 | 9 | 9 | 10 | 3 | 5.67 | 9 | 7 | 9 | 10 | 3 | 5 | 7 |
AC-4 | 7 | 9 | 10 | 0 | 1 | 1 | 7 | 9 | 10 | 5 | 7 | 9 |
Table 10Normalized fuzzy decision matrix (R~)
Consultant | Experience of consultant (C1) | Methodology (C2) | Qualification of key personnel (C3) | Transfer of knowledge (C4) | ||||||||
AC-1 | 0.5 | 0.7 | 0.9 | 0.5 | 0.83 | 1 | 0.7 | 0.9 | 1 | 0.7 | 0.9 | 1 |
AC-2 | 0.9 | 0.9 | 1 | 0.7 | 0.9 | 1 | 0.5 | 0.7 | 0.9 | 0.7 | 0.9 | 1 |
AC-3 | 0.9 | 0.9 | 1 | 0.3 | 0.57 | 0.9 | 0.7 | 0.9 | 1 | 0.3 | 0.5 | 0.7 |
AC-4 | 0.7 | 0.9 | 1 | 0 | 0.1 | 0.1 | 0.7 | 0.9 | 1 | 0.5 | 0.7 | 0.9 |
Table 11Weighted normalized fuzzy decision matrix (V~)
Weightage () | 0.180 | 0.332 | 0.587 | 0.121 | 0.211 | 0.397 | 0.200 | 0.363 | 0.632 | 0.058 | 0.094 | 0.172 |
Consultant | Experience of consultant (C1) | Methodology (C2) | Qualification of key personnel (C3) | Transfer of knowledge (C4) | ||||||||
AC-1 | 0.090 | 0.232 | 0.528 | 0.060 | 0.176 | 0.397 | 0.140 | 0.327 | 0.632 | 0.041 | 0.085 | 0.172 |
AC-2 | 0.162 | 0.299 | 0.587 | 0.085 | 0.190 | 0.397 | 0.100 | 0.254 | 0.569 | 0.041 | 0.085 | 0.172 |
AC-3 | 0.162 | 0.299 | 0.587 | 0.036 | 0.120 | 0.357 | 0.140 | 0.327 | 0.632 | 0.017 | 0.047 | 0.121 |
AC-4 | 0.126 | 0.299 | 0.587 | 0.000 | 0.021 | 0.040 | 0.140 | 0.327 | 0.632 | 0.029 | 0.066 | 0.155 |
FPIS (A*) | 0.162 | 0.299 | 0.587 | 0.085 | 0.190 | 0.397 | 0.140 | 0.327 | 0.632 | 0.041 | 0.085 | 0.172 |
FNIS (A-) | 0.090 | 0.232 | 0.528 | 0.000 | 0.021 | 0.040 | 0.100 | 0.254 | 0.569 | 0.017 | 0.047 | 0.121 |
Table 12Distance (d*) and sum of distance (Si*) from FPIS
Consultant | Distance from FPIS () | ||||
AC-1 | 0.066 | 0.016 | 0.000 | 0.000 | 0.082 |
AC-2 | 0.000 | 0.000 | 0.060 | 0.000 | 0.060 |
AC-3 | 0.000 | 0.054 | 0.000 | 0.039 | 0.094 |
AC-4 | 0.021 | 0.233 | 0.000 | 0.016 | 0.270 |
Table 13Distance (d-) and sum of distance (Si-) from FNIS
Consultant | Distance from FNIS () | ||||
AC-1 | 0.000 | 0.227 | 0.060 | 0.039 | 0.327 |
AC-2 | 0.066 | 0.233 | 0.000 | 0.039 | 0.338 |
AC-3 | 0.066 | 0.193 | 0.060 | 0.000 | 0.319 |
AC-4 | 0.055 | 0.000 | 0.060 | 0.024 | 0.139 |
Table 14Closeness coefficient (Cci*) and rank of consultant
Consultant | Rank | |
Consultant 1 (AC-1) | 0.7991 | 2 |
Consultant 2 (AC-2) | 0.8490 | 1 |
Consultant 3 (AC-3) | 0.7731 | 3 |
Consultant 4 (AC-4) | 0.3398 | 4 |
4.3. Rank comparison of fuzzy TOPSIS with current practices
From the DWRI model, the ranking of consultant as per current practices was obtained. The equivalence ranking for the Fuzzy AHP was generated on the basis of the deviations implied by the weightage obtained over actual practices. The ranking between the Fuzzy TOPSIS, equivalence Fuzzy AHP and actual practice were compared which is shown in Table 15.
Table 15Rank comparison between model and actual practices
Consultant | Fuzzy TOPSIS | Fuzzy AHP | Current practices |
Consultant 1 (AC-1) | 2 | 3 | 1 |
Consultant 2 (AC-2) | 1 | 1 | 2 |
Consultant 3 (AC-3) | 3 | 2 | 3 |
Consultant 4 (AC-4) | 4 | 4 | 4 |
The rankings from the Fuzzy TOPSIS and Fuzzy AHP methods are consistent, with consultant 2 (AC-2) being ranked the highest in both cases. This indicates that Consultant 2 (AC-2) is perceived as the most favorable option according to both evaluation methods. Consultant 1 (AC-1) performs well according to the Current Practices ranking, indicating that it is currently favored based on existing evaluation methods. The discrepancy between the rankings of Consultant 1 (AC-1) and Consultant 2 (AC-2) between the Fuzzy TOPSIS/Fuzzy AHP methods and Current Practices suggests a potential for improvement in the current evaluation practices, as the methods employing Fuzzy TOPSIS and Fuzzy AHP may provide a more robust and objective evaluation of consultants.
5. Conclusions
In this study, we introduce a novel consultant selection model for technical proposals and ranking within DWRI, employing a hybrid approach of fuzzy AHP and fuzzy TOPSIS for the first time. Initially, utilizing the Fuzzy Analytic Hierarchy Process (AHP), we determined the weights of both criteria and sub-criteria. Furthermore, we conducted a comparative analysis between the consultant rankings derived from conventional practices and those derived from the Fuzzy Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) model. The findings reveal a general consistency in the criteria weightages for consultant selection between conventional practices and the perspectives within DWRI.
While the sample size and study area may limit the generalizability of the results, this approach offers valuable insights into criteria, sub-criteria, and weightage using the Fuzzy AHP tool. The variation in consultant ranking between the Fuzzy TOPSIS model and current practices underscores the importance of revisiting criteria and weightages. Moving forward, DWRI should consider the findings of this research. Future studies should aim to include larger sample sizes and employ advanced tools such as Analytic Network Process (ANP) and PROMETHEE to further enhance understanding. Selecting a competent consultant remains a challenge due to the qualitative nature of decision criteria, but with appropriate criteria, sub-criteria, weightage, and the right tools and judgment, efficient selection processes can be established.
References
-
D. Singh and R. L. K. Tiong, “A fuzzy decision framework for contractor selection,” Journal of Construction Engineering and Management, Vol. 131, No. 1, pp. 62–70, Jan. 2005, https://doi.org/10.1061/(asce)0733-9364(2005)131:1(62)
-
R. Karki, “A study of criteria for selection of consultant in Nepal,” 2019.
-
M. K. Trivedi, M. K. Pandey, and S. S. Bhadoria, “Prequalification of construction contractor using a FAHP,” International Journal of Computer Applications, Vol. 28, No. 10, pp. 39–45, Aug. 2011, https://doi.org/10.5120/3424-4773
-
L.-S. Chen and C.-H. Cheng, “Selecting IS personnel use fuzzy GDSS based on metric distance method,” European Journal of Operational Research, Vol. 160, No. 3, pp. 803–820, Feb. 2005, https://doi.org/10.1016/j.ejor.2003.07.003
-
S. Khoshfetrat, F. Hosseinzadeh Lotfi, S. Khoshfetrat, and F. Hosseinzadeh-Lotfi, “Deriving priorities, the alternatives in an analytic hierarchy process,” International Journal of Research in Industrial Engineering, Vol. 3, No. 4, pp. 13–20, 2014.
-
C.-A. Tsai, S. W. Lo, and T.-M. Lin, “An analytical framework with sensitivity analysis to quantify management consultancy selection,” International Journal of the Analytic Hierarchy Process, Vol. 5, No. 1, Jul. 2013, https://doi.org/10.13033/ijahp.v5i1.167
-
F. K. T. Cheung, J. L. F. Kuen, and M. Skitmore, “Multi-criteria evaluation model for the selection of architectural consultants,” Construction Management and Economics, Vol. 20, No. 7, pp. 569–580, Oct. 2002, https://doi.org/10.1080/01446190210159818
-
A. Kazaz, M. Talat Birgonul, T. Acıkara, B. Er, M. Talat Birgönül, and H. Kaplan, “Evaluation of consulting firms selection in construction projects by using fuzzy logic,” International Conference on Engineering and Natural Sciences, 2016.
-
T. T. Ha, L. L. Hoai, and Y. D. Lee, “A fuzzy AHP model for selection of consultant contractor in bidding phase in Vietnam,” Journal of Construction Engineering and Project Management, Vol. 5, No. 2, pp. 35–43, Jun. 2015, https://doi.org/10.6106/jcepm.2015.5.2.035
-
A. Nieto-Morote and F. Ruz-Vila, “A fuzzy multi-criteria decision-making model for construction contractor prequalification,” Automation in Construction, Vol. 25, pp. 8–19, Aug. 2012, https://doi.org/10.1016/j.autcon.2012.04.004
-
San Cristóbal and José Ramón, “Contractor selection using multicriteria decision-making methods,” Journal of Construction Engineering and Management, Vol. 138, No. 6, pp. 751–758, Jun. 2012, https://doi.org/10.1061/(asce)co.1943-7862.0000488
-
M. Dursun and E. E. Karsak, “A fuzzy MCDM approach for personnel selection,” Expert Systems with Applications, Vol. 37, No. 6, pp. 4324–4330, Jun. 2010, https://doi.org/10.1016/j.eswa.2009.11.067
-
A. Kelemenis, K. Ergazakis, and D. Askounis, “Support managers’ selection using an extension of fuzzy TOPSIS,” Expert Systems with Applications, Vol. 38, No. 3, pp. 2774–2782, Mar. 2011, https://doi.org/10.1016/j.eswa.2010.08.068
-
“2009 IEEE International Conference on Systems, Man and Cybernetics,” in 2009 IEEE International Conference on Systems, Man and Cybernetics – SMC, Oct. 2009, https://doi.org/10.1109/smc12345.2009
-
C.-N. Liao, “An evaluation model using fuzzy TOPSIS and goal programming for TQM consultant selection,” Journal of Testing and Evaluation, Vol. 41, No. 1, pp. 1–9, Jan. 2013, https://doi.org/10.1520/jte104563
-
M. Saremi, S. F. Mousavi, and A. Sanayei, “TQM consultant selection in SMEs with TOPSIS under fuzzy environment,” Expert Systems with Applications, Vol. 36, No. 2, pp. 2742–2749, Mar. 2009, https://doi.org/10.1016/j.eswa.2008.01.034
-
J. A. Goguen, “L. A. Zadeh. Fuzzy sets. Information and control, vol. 8 (1965), pp. 338-353. – L. A. Zadeh. Similarity relations and fuzzy orderings. Information sciences, vol. 3 (1971), pp. 177-200,” Journal of Symbolic Logic, Vol. 38, No. 4, pp. 656–657, Mar. 2014, https://doi.org/10.2307/2272014
-
T. L. Saaty, “Analytic hierarchy process,” in Encyclopedia of Biostatistics, Wiley, 2005, https://doi.org/10.1002/0470011815.b2a4a002
-
P. Ashoka Varthanan, N. Murugan, and G. Mohan Kumar, “An AHP based heuristic DPSO algorithm for generating multi criteria production-distribution plan,” Journal of Manufacturing Systems, Vol. 32, No. 4, pp. 632–647, Oct. 2013, https://doi.org/10.1016/j.jmsy.2013.05.014
-
C.-L. Hwang and K. Yoon, Lecture Notes in Economics and Mathematical Systems. Berlin, Heidelberg: Springer Berlin Heidelberg, 1981, https://doi.org/10.1007/978-3-642-48318-9
-
J. J. Buckley, T. Feuring, and Y. Hayashi, “Fuzzy hierarchical analysis,” Proceedings of 8th International Fuzzy Systems Conference, Vol. 17, pp. 1009–1013 vol.2, Jan. 1999, https://doi.org/10.1109/fuzzy.1999.793090
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Nischal Silwal: data curation, methodology, formal analysis, software, resources, writing – original draft preparation and visualization. Subash Kumar Bhattarai: conceptualization, methodology, formal analysis, project administration, supervision, validation, and writing – review and editing. Dinesh Sukamani: conceptualization, resources, investigation, validation, visualization, and project administration.
The authors declare that they have no conflict of interest.
