Generalised Poisson-new linear-exponential distribution

Sah, Binod Kumar; Sahani, Suresh Kumar

doi:10.21595/mme.2024.24258

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 08 September 2024

Check for updates

Generalised Poisson-new linear-exponential distribution

Binod Kumar Sah¹

Suresh Kumar Sahani²

¹Department of Statistics, R. R. M. Campus, Tribhuvan University, Janakpurdham, Nepal

²Department of Science and Technology, Rajarshi Janak University, Janakpurdham, Nepal

Corresponding Author:

Suresh Kumar Sahani

Cite the article Download PDF

Article in Press

Downloads 43

Abstract

It is a compound discrete probability distribution which has two parameters and whose particular case is Poisson-New Linear-Exponential Distribution (PNLED) [1]. The statistical characteristics required for this distribution such as probability mass function (pmf), statistical moments, estimation of parameters and goodness of fit have been derived and explained nicely. To test theoretical reliability of this distribution, goodness of fit has been applied to some over-dispersed data which were used by other researchers and further, we found that this distribution looks more appropriate for statistical modelling than PNLED, generalised Poisson-Lindley distribution (GPLD) [1, 2] and Poisson-Lindley distribution (PLD) [3].

1. Introduction

A generalisation of any probability distribution is considered more appropriate when it is more reliable than its particular case as well as previously obtained generalised distribution with similar conditions in all aspects.

The proposed distribution is a compound distribution. For compounding process, at least two distributions are required. We have needed Generalised Poisson distribution (GPD) [4] and New Linear-exponential distribution (NLED) [5] to conduct compounding process. GPD [4] distribution is a discrete distribution whereas NLED [5] is a continuous distribution. GPD [4] has two parameters and in mixing process it plays role of an original distribution and its original parameter $λ$ follows NLED [5]. The pmf of GPD [4] has been given by:

1

P_{1} (Z; λ, θ) = \frac{λ (λ + θ z)^{z - 1} e^{- (λ + θ z)}}{z!},

where $Z = 0,1, 2, \dots$ ; $λ > 0$ ; $| θ | < 1$ .

The probability density function (pdf) of NLED [5] was given by:

2

f_{2} (z; β) = \frac{β^{2}}{(1 + π β)} (π + β) e^{- β y}, z > 0, β > 0 .

Hence, Generalised Poisson-New Linear-exponential distribution (GPNLED) has been obtained by compounding GPD [4] with NLED [5]. The study of this papers mentioned in the following references [1, 2], [4], [6] have very much contributed to increase quality of the paper.

In this paper, the following works have been done. Construction and derivation of:

1) Probability Mass Function (pmf) of GPNLED.

2) Statistical Moments of GPNLED.

3) Estimation of Parameters of GPNLED.

4) Goodness of Fit and applications of GPNLED.

We have been studied the following papers to improve quality of this paper which have been mentioned in the following references [2], [7-14].

2. Results

The results obtained for this paper have been placed under the following sub-headings.

2.1. Probability mass function of GPNLED

GPD has two parameters $λ$ and $θ$ . $λ$ is an original parameter of GPD which follows NLED. $θ$ is an additional parameter of GPD which is versatile in nature and hence, GPD. Here, $λ > 0$ and | $θ$ | < 1. NLED has a single parameter $β$ . The Probability mass of function of GPNLED is obtained by mixing GPD with NLED. This is how the pmf of GPNLED have been extracted:

3

P (Z; β, θ) = [\frac{β^{2} e^{- θ z}}{z! (1 + π β)}] \int_{0}^{\infty} \{\sum_{i = 1}^{z - 1} (\begin{matrix} z - 1 \\ i \end{matrix}) {(\frac{θ z}{1})}^{i} (π λ^{z - i} + λ^{z - i + 1}) e^{- λ (1 + β)}\} d λ

= [\frac{β^{2} e^{- θ z}}{z! (1 + π β)}] \{\sum_{i = 0}^{z - 1} \frac{(z - 1)!}{i! (z - i - 1)!} {(\frac{θ z}{1})}^{i} (\frac{π Γ (z - i + 1)}{(1 + β)^{z - i + 1}} + \frac{π Γ (z - i + 2)}{(1 + β)^{z - i + 2}})\}

= [\frac{β^{2} e^{- θ z}}{z (1 + π β)}] \{\sum_{i = 0}^{z - 1} (\frac{θ^{i} z^{i}}{i! (z - i - 1)!}) (\frac{Γ (z - i + 1)}{(1 + β)^{z - i + 1}}) (π + \frac{(z - i + 1)}{(1 + β)})\}

= [\frac{β^{2} e^{- θ z}}{(1 + π β)}] \{\sum_{i = 0}^{z - 1} (\frac{θ^{i} z^{i - 1}}{i!}) (\frac{(z - i)}{(1 + β)^{z - i + 2}}) (π (1 + β) + (z - i + 1))\}

= [\frac{β^{2} e^{- θ z}}{(1 + π β)}] [\frac{\{π (1 + β) + (z + 1)\}}{(1 + β)^{z + 2}}] + [\frac{β^{2} e^{- θ z}}{(1 + π β)}] \{\sum_{i = 1}^{z - 1} (\frac{θ^{i} z (z - i)^{i - 1}}{i!}) (\frac{\{π (1 + β) + (z - i + 1)\}}{(1 + β)^{z - i + 2}})\}

z = 0,1, 2, . . ., λ > 0, β > 0 .

Probability mass function of GPNLED can be obtained for each value such as $z = 0,1, 2, . . .$ can be obtained by using the Eq. (3) as follows:

4

P (z = 0) = [\frac{β^{2}}{(1 + π β)}] [\frac{\{π (1 + β) + 1\}}{(1 + β)^{2}}],

5

P (z = 1) = [\frac{β^{2} e^{- θ}}{(1 + π β)}] [\frac{\{π (1 + β) + 2\}}{(1 + β)^{3}}],

6

P (z = 2) = [\frac{β^{2} e^{- 2 θ}}{(1 + π β)}] [\frac{\{π (1 + β) + 3\}}{(1 + β)^{4}} + \frac{θ \{π (1 + β) + 2\}}{(1 + β)^{3}}],

7

P (z = 3) = [\frac{β^{2} e^{- 3 θ}}{(1 + π β)}] [\frac{\{π (1 + β) + 4\}}{(1 + β)^{5}} + \frac{2 θ \{π (1 + β) + 3\}}{(1 + β)^{4}} + \frac{1.5 θ^{2} \{π (1 + β) + 2\}}{(1 + β)^{3}}],

8

P (z = 4) = [\frac{β^{2} e^{- 4 θ}}{(1 + π β)}] [\frac{\{π (1 + β) + 5\}}{(1 + β)^{6}} + \frac{3 θ \{π (1 + β) + 4\}}{(1 + β)^{5}} + \frac{4 θ^{2} \{π (1 + β) + 3\}}{(1 + β)^{4}}

+ \frac{16 θ^{3} \{π (1 + β) + 2\}}{6 (1 + β)^{3}}],

9

P (z = 5) = [\frac{β^{2} e^{- 5 θ}}{(1 + π β)}] [\frac{\{π (1 + β) + 6\}}{(1 + β)^{7}} + \frac{4 θ \{π (1 + β) + 5\}}{(1 + β)^{6}} + \frac{15 θ^{2} \{π (1 + β) + 4\}}{2 (1 + β)^{5}}

+ \frac{50 θ^{3} \{π (1 + β) + 3\}}{6 (1 + β)^{4}} + \frac{125 θ^{4} \{π (1 + β) + 2\}}{24 (1 + β)^{3}}] .

2.2. Statistical moments of GPNLED

Let ${μ_{r}}^{'}$ denotes $r$ th moment about origin of GPNLED:

10

{μ'}_{r} = E [E (Z^{r} / λ] = \frac{β^{2}}{(1 + π β)} \int_{0}^{\infty} (\sum_{z = 0}^{\infty} \frac{z^{r} λ (λ + θ z)^{z - 1} e^{- (λ + θ z)} λ^{z}}{Γ (z + 1)}) (π + λ) e^{- β λ} d λ,

11

{μ'}_{1} = \frac{β^{2}}{(1 + π β)} \int_{0}^{\infty} (\sum_{z = 0}^{\infty} \frac{z^{1} λ (λ + θ z)^{z - 1} e^{- (λ + θ z)} λ^{z}}{Γ (z + 1)}) (π + λ) e^{- β λ} d λ = \frac{β^{2}}{(1 + π β)} \int_{0}^{\infty} \frac{λ}{(1 + θ)} (π + λ) e^{- β λ} d λ = \frac{(π β + 2)}{β (1 + π β) (1 - θ)} .

Fig. 1Showing the mean of GPNLED

12

{μ'}_{2} = \frac{β^{2}}{(1 + π β)} \int_{0}^{\infty} (\sum_{z = 0}^{\infty} \frac{z^{2} λ (λ + θ z)^{z - 1} e^{- (λ + θ z)} λ^{z}}{Γ (z + 1)}) (π + λ) e^{- β λ} d λ = \frac{β^{2}}{(1 + π β)} \int_{0}^{\infty} \{\frac{λ}{(1 - θ)^{3}} + \frac{λ^{2}}{(1 - θ)^{2}}\} (π + λ) e^{- β λ} d λ = \frac{[β (π β + 2) + 2 (1 - θ) (π β + 3)]}{β^{2} (π β + 1) (1 - θ)^{3}} .

13

{μ'}_{3} = \frac{β^{2}}{(1 + π β)} \int_{0}^{\infty} (\sum_{z = 0}^{\infty} \frac{z^{3} λ (λ + θ z)^{z - 1} e^{- (λ + θ z)} λ^{z}}{Γ (z + 1)}) (π + λ) e^{- β λ} d λ = \frac{β^{2}}{(1 + π β)} \int_{0}^{\infty} \{\frac{(1 + 2 θ) λ}{(1 - θ)^{5}} + \frac{3 λ^{2}}{(1 - θ)^{4}} + \frac{λ^{3}}{(1 - θ)^{3}}\} (π + λ) e^{- β λ} d λ = \frac{(1 + 2 θ) (π β + 2)}{β (1 + π β) (1 - θ)^{5}} + \frac{2 (π β + 3)}{β^{2} (1 + π β) (1 - θ)^{4}} + \frac{6 (π β + 4)}{β^{3} (1 + π β) (1 - θ)^{5}} .

14

{μ'}_{4} = \frac{β^{2}}{(1 + π β)} \int_{0}^{\infty} (\sum_{z = 0}^{\infty} \frac{z^{4} λ (λ + θ z)^{z - 1} e^{- (λ + θ z)} λ^{z}}{Γ (z + 1)}) (π + λ) e^{- β λ} d λ = \frac{β^{2}}{(1 + π β)} \int_{0}^{\infty} \{\frac{(1 + 8 θ + 6 θ^{2}) λ}{(1 - θ)^{7}} + \frac{(7 + 8 θ) λ^{2}}{(1 - θ)^{6}} + \frac{6 λ^{3}}{(1 - θ)^{5}} + \frac{λ^{4}}{(1 - θ)^{4}}\} (π + λ) e^{- β λ} d λ = \frac{(1 + 8 θ + 6 θ^{2}) (π β + 2)}{β (1 + π β) (1 - θ)^{7}} + \frac{2 (7 + 8 θ) (π β + 3)}{β^{2} (1 + π β) (1 - θ)^{6}} + \frac{(6) (6) (π β + 4)}{β^{3} (1 + π β) (1 - θ)^{5}} + \frac{24 (π β + 5)}{β^{4} (1 + π β) (1 - θ)^{4}} .

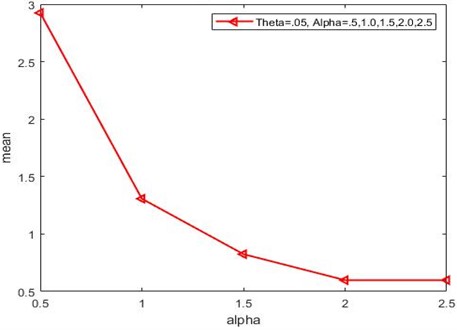
Central moments of GPNLED:

15

μ_{2} = E (z^{2}) - {\{E (z)\}}^{2} = \frac{[β (π β + 2) + 2 (1 - θ) (π β + 3)]}{β^{2} (π β + 1) (1 - θ)^{3}} - {(\frac{(π β + 2)}{α (π β + 1) (1 - θ)})}^{2} = \frac{[π^{2} β^{3} + π^{2} β^{2} + 3 π β^{2} + (4 π + 2) β + 2] - θ (π^{2} β^{3} + 4 π β + 2)}{[β (π β + 1)]^{2} (1 - θ)^{3}} .

Fig. 2Showing the variance of GPNLED

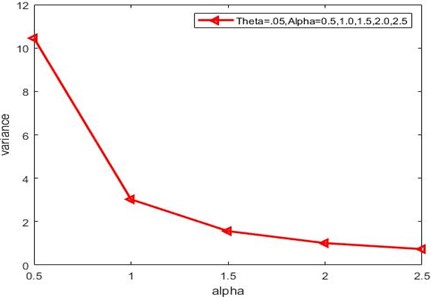
Proof. Variance > Mean.

Or:

\frac{[π^{2} β^{3} + π^{2} β^{2} + 3 π β^{2} + (4 π + 2) β + 2] - θ (π^{2} β^{3} + 4 π β + 2)}{[β (π β + 1)]^{2} (1 - θ)^{3}} > \frac{(π β + 2)}{β (1 + π β) (1 - θ)} .

Or:

(π^{2} β^{3} + 3 π β^{2} + 2 β) + (1 - θ) \{(π^{2} α^{2} + 4 π α + 2) - (π β^{2} + 2 β) (1 + π β) (1 - θ)\} > 0 .

Or $:$

(1 - θ) \{(π^{2} α^{2} + 4 π α + 2) - (π β^{2} + 2 β) (1 + π β) (1 - θ)\} > 0 .

Or:

16

(1 - θ) \leq \frac{(π^{2} β^{2} + 4 π β + 2)}{(π^{2} β^{3} + 3 π β^{2} + 2 β)} .

Hence the statement.

The third moment about the mean of this distribution can be obtained as:

17

μ_{3} = E (z^{3}) - 3 E (z^{2}) E (z) + 2 {\{E (z)\}}^{3} = [\frac{(1 + 2 θ) (π β + 2)}{β (1 + π β) (1 - θ)^{5}} + \frac{2 (π β + 3)}{β^{2} (1 + π β) (1 - θ)^{4}} + \frac{6 (π β + 4)}{β^{3} (1 + π β) (1 - θ)^{5}}] - 3 [\frac{[β (π β + 2) + 2 (1 - θ) (π β + 3)]}{β^{2} (π β + 1) (1 - θ)^{3}}] [\frac{(π β + 2)}{β (1 + π β) (1 - θ)}] + 2 {[\frac{(π β + 2)}{β (1 + π β) (1 - θ)}]}^{3}

= \frac{[\begin{matrix} [\{β^{2} (1 + π β)^{2} (1 + 2 θ) (π β + 2)\} + \{3 (1 - θ) β (1 + π β)^{2} (2 π β + 6)\} \\ + \{(1 - θ)^{2} (1 + π β)^{2} (6 π β + 24)\}] \\ - [\{3 (1 - θ) β (1 + π β) (π β + 2)^{2}\} \{6 (1 - θ)^{2} (1 + π β) (π β + 2) (π β + 3)\} \\ + [\{2 (π β + 2)^{3}\}] \end{matrix}]}{[β (1 + π β)]^{3} (1 - θ)^{5}} .

The third central moment ( $μ_{3}$ ) gives positive value, this distribution is positively skewed in shape.

18

μ_{4} = E (z^{4}) - 4 E (z^{3}) E (z) + 6 E (z^{2}) {\{E (z)\}}^{2} - 3 {\{E (z)\}}^{4} = \frac{(1 + 8 θ + 6 θ^{2}) (π β + 2)}{β (1 + π β) (1 - θ)^{7}} + \frac{2 (7 + 8 θ) (π β + 3)}{β^{2} (1 + π β) (1 - θ)^{6}} + \frac{(6) (6) (π β + 4)}{β^{3} (1 + π β) (1 - θ)^{5}} + \frac{24 (π β + 5)}{β^{4} (1 + π β) (1 - θ)^{4}} - 4 [\frac{(1 + 2 θ) (π β + 2)}{β (1 + π β) (1 - θ)^{5}} + \frac{2 (π β + 3)}{β^{2} (1 + π β) (1 - θ)^{4}}

+ \frac{6 (π β + 4)}{β^{3} (1 + π β) (1 - θ)^{5}}] [\frac{(π β + 2)}{β (1 + π β) (1 - θ)}] + 6 [\frac{[β (π β + 2) + 2 (1 - θ) (π β + 3)]}{β^{2} (π β + 1) (1 - θ)^{3}}] {[\frac{(π β + 2)}{β (1 + π β) (1 - θ)}]}^{2} - 3 {[\frac{(π β + 2)}{β (1 + π β) (1 - θ)}]}^{4}

= \frac{[\begin{matrix} [{(1 + 8 θ + 6 θ^{2}) β^{3} (1 + π β)^{3} (π β + 2)\} \\ + {(7 + 8 θ) (1 - θ) β^{2} (1 + π β)^{3} (2 π β + 6)} \\ + {6 (1 - θ)^{2} β (1 + π β)^{3} (6 π β + 24)\} + \{(1 - θ)^{3} (1 + π β)^{3} (24 π β + 120)\}] \\ - 4 (1 - θ) (π β + 2) [\{(1 + 2 θ) β^{2} (2 + π β)\} \\ + \{3 (1 - θ) β (2 π β + 6)\} + (1 - θ)^{2} (6 π β + 24)] \\ + 6 (1 - θ)^{2} (π β + 1) (π β + 2)^{2} [{β (2 + π β) + 2 (1 - θ) (3 + π β)}] \\ - 3 (1 - θ)^{3} (π β + 2)^{4} \end{matrix}]}{[β (1 + π β)]^{4} (1 - θ)^{7}} .

The Eq. (18) is obtained to know about nature of distribution according to size and it is the fourth central moment. Co-efficient of skewness and kurtosis based on moments can be obtained as follows.

19

γ_{1} = \frac{μ_{3}}{(μ_{2})^{3 / 2}} = \frac{[\begin{matrix} [\{β^{2} (1 + π β)^{2} (1 + 2 θ) (π β + 2)\} + \{3 (1 - θ) β (1 + π β)^{2} (2 π β + 6)\} \\ + \{(1 - θ)^{2} (1 + π β)^{2} (6 π β + 24)\}] \\ - [\{3 (1 - θ) β (1 + π β) (π β + 2)^{2}\} + \{6 (1 - θ)^{2} (1 + π β) (π β + 2) (π β + 3)\}] \\ + [\{2 (1 - θ)^{2} (π β + 2)^{3}\}] \end{matrix}]}{(1 - θ)^{1 / 2} [[π^{2} β^{3} + π^{2} β^{2} + 3 π β^{2} + (4 π + 2) β + 2] - θ (π^{2} β^{3} + 4 π β + 2)]^{3 / 2}} .

From Eq. (19), it has been found that range of $γ_{1}$ is $(\sqrt{2}) < γ_{1} < \infty)$ . Hence, it is positively skewed:

20

β_{2} = \frac{μ_{4}}{(μ_{2})^{2}} = \frac{[\begin{matrix} [\{(1 + 8 θ + 6 θ^{2}) β^{3} (1 + π β)^{3} (π β + 2)\} \\ + \{(7 + 8 θ) (1 - θ) β^{2} (1 + π β)^{3} (2 π β + 6)\} \\ + \{6 (1 - θ)^{2} β (1 + π β)^{3} (6 π β + 24)\} + \{(1 - θ)^{3} (1 + π β)^{3} (24 π β + 120)\}] \\ - 4 (1 - θ) (π β + 2) [\{(1 + 2 θ) β^{2} (2 + π β)\} + \{3 (1 - θ) β (2 π β + 6)\} \\ + (1 - θ)^{2} (6 π β + 24) \\ + 6 (1 - θ)^{2} (π β + 1) (π β + 2)^{2} [\{β (2 + π β) + 2 (1 - θ) (3 + π β)\}] \\ - 3 (1 - θ)^{3} (π β + 2)^{4} \end{matrix}]}{(1 - θ)^{1 / 2} [[π^{2} β^{3} + π^{2} β^{2} + 3 π β^{2} + (4 π + 2) β + 2] - θ (π^{2} β^{3} + 4 π β + 2)]^{3 / 2}} .

2.3. Estimation of parameters

This distribution has two parameters $β$ and $θ$ which can be obtained as

By using $P (z = 0)$ and ${μ_{1}}^{'}$ . We have:

P (z = 0) = [\frac{β^{2}}{(1 + π β)}] [\frac{\{π (1 + β) + 1\}}{(1 + β)^{2}}] .

Solving it, we get:

21

f (β) = π (1 - k) β^{3} + (1 + π - k - 2 π k) β^{2} - k (2 + π) β - k = 0 .

The Polynomial Eq. (21) can be solved by using Regula-Falshi method or Newton Rapson method, where $k$ denote $P (z = 0)$ .Substituting the estimated value of $β$ in the following Eq. (22), we get an estimated value of $θ$ :

22

(1 - θ) = \frac{(π β + 2)}{[{μ_{1}}^{'} β (1 + π β)]} .

${μ_{1}}^{'}$ and ${μ_{2}}^{'}$ : substituting the value of $(1 - θ)$ obtained from Eq. (22) in the expression of ${μ_{2}}^{'}$ , we get Polynomial Eq. (23) in $β$ which can be solve by Newton-Rapson or Regla-Falsi method:

23

f (β) = {μ_{2}}^{'} (π β + 2)^{3} - ({μ_{1}}^{'})^{2} (π β + 1) (π β + 2) \{{μ_{1}}^{'} β^{2} (π β + 1) + 2 (π β + 3)\} = 0 .

2.4. Goodness of fit and applications of GPNLED

This distribution can be used to test goodness of fit and to get possible inferential Statistics in the field related to accident proneness, risk management of production engineering, ecological sciences, agricultural fields related to events about insects, error per page, biological sciences, and other fields [15-17].

Applications of GPNLE model in the field of engineering. This distribution is applicable to fit better where Poisson, Generalised Poisson and Poisson mixtures of continuous distributions are applicable such as:

1) The count of $α$ -particles emitted per unit of time is useful in analysis of any radio-active substances.

2) Number of telephone calls received on a given switch board per small unit of time.

3) In industrial production to find the proportion of defects per unit length, per unit area, etc.

4) In the field of reliability engineering.

In the following examples Chi-square goodness of fit have been applied by using GPNLE model.

Table 1Example (1)

Z	0	1	2	3	$4^{+}$
Observed frequency	35	11	8	4	2

Table 2Example (2)

Number of accidents	0	1	2	3	4	5⁺
Observed frequency	447	132	42	21	3	2

Table 3Example (3)

Z	0	1	2	3	4	5	6
Observed frequency	200	57	30	7	4	0	2

The first example is related to the number of errors per page which was given by Kemp and Kemp [18]. The second example is related to the data of accidents to 647 women working on H. E. Shells in 5 weeks was given by Greenwood and Yule [19]. The data related to Class per exposure (μg/kg) which is included in example (3) was given by Catcheside et al. [20].

The first and second examples have been used in the Doctoral Thesis. The theoretical frequencies obtained by using PLD, GPLD and GPNLED have been placed in Table 4 and 5 to make comparison. In Table 6, the theoretical frequencies obtained by using PLD, PNLED and GPNLED have been placed for comparison [1-3].

Table 4Observed versus expected frequency of example (1)

Number of errors per page	Observed frequency	Expected frequency
Number of errors per page	Observed frequency	PLD	GPLD	GPNLED
0	35	33.0	35.0	35.0
1	11	15.3	13.3	13.3
2	8	6.8	6.3	6.4
3	4	2.9	3.0	2.9
4⁺	2	2.0	2.4	2.4
	60.0	60.0	60.0	647.0
${μ_{1}}^{'}$	0.7833333	–	–	–
${μ_{2}}^{'}$	1.85	–	–	–
$\hat{β}$	–	1.7434	1.9387733	1.642188744
$\hat{θ}$	–	–	0.1174867	0.09640955

Table 5Observed versus expected frequency of example (2)

Number of accidents	Observed frequency	Expected frequency
Number of accidents	Observed frequency	PLD	GPLD	GPNLED
0	447	441	447.0	447.0
1	132	143	1132.7	132.9
2	42	45	44.8	45.0
3	21	14	15.1	15.0
4	3	4	5.0	5.0
5⁺	2	1	2.4	2.1
	647	647	647.0	647.0
${μ_{1}}^{'}$	0.4652241	–	–	–
${μ_{2}}^{'}$	0.9100646	–	–	–
$\hat{β}$	–	–	2.8563455	2.496217
$\hat{θ}$	–	–	0.0523222	0.0415098

Table 6Observed versus expected frequency of example (3)

Class per exposure (μg/kg)	Observed frequency	Expected frequency
Class per exposure (μg/kg)	Observed frequency	PLD	PNLED	GPNLED
0	200	191.8	192.8	200.0
1	57	70.3	69.2	60.5
2	30	24.9	24.6	23.7
3	7	8.6	8.7	9.5
4	4	2.9	3.1	3.8
5	0	1.0	1.1	1.5
6	2	0.5	0.5	1.0
	300	300.0	300.0	300.0
${μ_{1}}^{'}$	0.55333333	–	–	–
${μ_{2}}^{'}$	1.2533333	–	–	–
$\hat{β}$	–	2.353339	2.0501155	2.256957115
$\hat{θ}$	–	–	–	0.1002898421

3. Conclusions

1) This distribution will be over-dispersed if $(1 - θ) \leq \frac{(π^{2} β^{2} + 4 π β + 2)}{(π^{2} β^{3} + 3 π β^{2} + 2 β)}$ .

2) The range of $γ_{1}$ is $(\sqrt{2}) < γ_{1} < \infty)$ . So, it is positively skewed in shape.

3) The range of $β_{2}$ is $6 < β_{2} < \infty$ . So, it is leptokurtic by size.

4) From the Tables 4 and 5, it is found that P-value obtained by using GPNLED is greater than those obtained by using GPLD [2] and PLD [3]

5) From Table 6, what we have observed that the P-value obtained by using GPNLED is bigger than those of PNLED [1] and PLD [3]

6) Hence, it is suggested to apply GPNLED instead of PLD, GPLD and PNLED in similar situation in all aspects.

References

B. K. Sah and S. K. Sahani, “Poisson-new quadratic-exponential distribution,” Mikailalsys Journal of Mathematics and Statistics, Vol. 2, No. 2, pp. 27–45, Apr. 2024, https://doi.org/10.58578/mjms.v2i2.2862

Publisher
B. K. Sah, “Generalisations of some countable and continuous mixtures of Poisson distribution and their applications,” Patna University, Patna, India, 2012.

Search CrossRef
M. Sankaran, “The discrete Poisson-Lindley distribution,” Biometrics, Vol. 26, pp. 145–149, Mar. 1970, https://doi.org/10.2307/2529053

Publisher
B. K. Sah, “New linear-exponential distribution,” Applied Science Periodical, Vol. 26, No. 2, pp. 1–16, May 2022.

Search CrossRef
P. C. Consul and G. C. Jain, “A generalization of the Poisson distribution,” Technometrics, Vol. 15, No. 4, pp. 791–799, Nov. 1973, https://doi.org/10.1080/00401706.1973.10489112

Publisher
M. Ahsanullah, “Two characterizations of the generalized Poisson distribution,” Pakistan Journal of Statistics, Vol. 7, pp. 15–19, 1971.

Search CrossRef
E. L. Lehmann and J. P. Romano, Testing of Statistical Hypothesis. New York: Springer, 2005.

Search CrossRef
A. Mishra, “Generalization of some discrete distributions,” Patna University, Patna, India, 1979.

Search CrossRef
B. K. Sah, “A generalised Neyman type – a distribution,” International Journal for Research in Applied Science and Engineering Technology, Vol. 9, No. 1, pp. 465–470, Jan. 2021, https://doi.org/10.22214/ijraset.2021.32839

Publisher
B. K. Sah, “A two-parameter quasi-Lindley mixture of generalised Poisson distribution,” International Journal of Mathematics and Statistics Invention, Vol. 3, No. 7, 2015.

Search CrossRef
B. K. Sah and S. K. Sahani, “Polynomial-exponential mixture of Poisson distribution,” Turkish Journal of Computer and Mathematics Education (TURCOMAT), Vol. 14, No. 3, Sep. 2023, https://doi.org/10.48047/tukomat/14.03.31

Publisher
M. M. Shoukri, “Estimation problems for some generalized discrete distributions,” Ph.D. Thesis, University of Calgary, Calgary, Canada, 1980.

Search CrossRef
M. J. Bollen, Understanding Power Quality Problems Voltages sags and Interruptions. New Jersey: IEEE Press, 2000.

Search CrossRef
B. K. Sah and A. Mishra, “On a generalised exponential-Lindley mixture of generalised Poisson distribution,” Nepalese Journal of Statistics, Vol. 4, pp. 33–42, Dec. 2020, https://doi.org/10.3126/njs.v4i0.33449

Publisher
I. R. Miller et al., Probability and Statistics for Engineers. New Jersey: Prentice Hall, 1990.

Search CrossRef
M. Sulaimon, “Application of linear regression model for Poisson distribution in forecasting,” Imperial Journal of Interdisciplinary Research, Vol. 1, No. 5, pp. 17–24, 2015.

Search CrossRef
D. R. Yates and D. J. Goodman, “Probability and stochastic processes: a friendly introduction for electrical and computer engineers,” Computers and Mathematics with Applications, Vol. 37, No. 6, p. 136, Mar. 1999, https://doi.org/10.1016/s0898-1221(99)90299-7

Publisher
C. D. Kemp and A. W. Kemp, “Some properties of the ’Hermite’ distribution,” Biometrika, Vol. 52, No. 3-4, pp. 381–394, Dec. 1965, https://doi.org/10.1093/biomet/52.3-4.381

Publisher
M. Greenwood and G. U. Yule, “An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks of disease or of repeated accidents,” Journal of the Royal Statistical Society, Vol. 83, No. 2, p. 255, Mar. 1920, https://doi.org/10.2307/2341080

Publisher
D. G. Catcheside, D. E. Lea, and J. M. Thoday, “The production of chromosome structural changes inTradescantia microspores in relation to dosage, intensity and temperature,” Journal of Genetics, Vol. 47, No. 2, pp. 137–149, Jan. 1946, https://doi.org/10.1007/bf02986783

Publisher

About this article

Received

15 June 2024

Accepted

27 July 2024

Published

08 September 2024

DOI

https://doi.org/10.21595/mme.2024.24258

Keywords

distribution

Poisson-new linear-exponential distribution

probability distribution

moments

proposed distribution

over-dispersed

goodness of fit

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Binod Kumar Sah: conceptualization, data curation, formal analysis, investigation, writing – original draft preparation. Suresh Kumar Sahani: conceptualization, data curation, formal analysis, investigation, supervision, writing – original draft preparation, writing – review and editing.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Research article

2023 10 20

Probabilistic seismic hazard analysis based on monthly maximum PGA distribution in three cities in southwest China

Dezhi Fang, Yinfeng Dong, Xiaoquan Xu

Research article

2020 06 30

Dynamic reliability sensitivity analysis for inter-story isolation structure under stochastic excitations

Shangrong Zhang, Fanglan Liu, Jianqiang Xiao, Yuchen Hu, Hairui Deng

Research article

2019 06 30

Inference of the optimal probability distribution model for geotechnical parameters by using Weibull and NID distributions

Fengqiang Gong, Tiancheng Wang, Shanyong Wang

Research article

2018 06 30

Remaining useful life prediction of the ball screw system based on weighted Mahalanobis distance and an exponential model

Juan Wen, Hongli Gao

B. K. Sah and S. K. Sahani, “Generalised Poisson-new linear-exponential distribution,” Mathematical Models in Engineering, Vol. 10, No. 4, –9, Sep. 2024, https://doi.org/10.21595/mme.2024.24258

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/mme.2024.24258
UR  - https://doi.org/10.21595/mme.2024.24258
TI  - Generalised Poisson-new linear-exponential distribution
T2  - Mathematical Models in Engineering
AU  - Sah, Binod Kumar
AU  - Sahani, Suresh Kumar
PY  - 2024
DA  - 2024/09/08
PB  - Extrica
VL  - 10
IS  - 4
SN  - 2351-5279
SN  - 2424-4627
ER  - 

Copy Ris

Copied to clipboard!

 @article{Sah_2024, title={Generalised Poisson-new linear-exponential distribution}, ISSN={2424-4627}, url={https://doi.org/10.21595/mme.2024.24258}, DOI={10.21595/mme.2024.24258}, journal={Mathematical Models in Engineering}, publisher={JVE International Ltd.}, author={Sah, Binod Kumar and Sahani, Suresh Kumar}, year={2024}, month=sep }

Copy Bibtex

Copied to clipboard!

[1]B. K. Sah and S. K. Sahani, “Generalised Poisson-new linear-exponential distribution,” Mathematical Models in Engineering, Sep. 2024, doi: 10.21595/mme.2024.24258.

Copy IEEE

Copied to clipboard!

Sah, Binod Kumar, and Suresh Kumar Sahani. “Generalised Poisson-New Linear-Exponential Distribution.” Mathematical Models in Engineering, September 8, 2024. https://doi.org/10.21595/mme.2024.24258.

Copy Chicago

Copied to clipboard!

Generalised Poisson-new linear-exponential distribution

Abstract

1. Introduction

2. Results

2.1. Probability mass function of GPNLED

2.2. Statistical moments of GPNLED

2.3. Estimation of parameters

2.4. Goodness of fit and applications of GPNLED

3. Conclusions

References

About this article

Related Articles