Design and analysis of tracking differentiator based on SO(3)

2.1. Concept of SO(3)

The SO(3) group is composed of all linear transformations in the three-dimensional Euclidean space that preserve the coordinate vectors unchanged [12]:

2.2. SO(3) kinematics model

According to the definition of SO(3), we have $R{R}^T=I=R^{T}R$, and by taking the derivative:

This implies that ${\dot{R}}^{T}R$ is a skew-symmetric matrix, which can be used to represent a small rotational displacement.

We use SO(3) to denote the set of 3×3 skew-symmetric matrices, also known as the Lie algebra of SO(3), where the general form of such a skew-symmetric matrix is:

Therefore, there must exist an $\mathrm{\Omega }$ such that $R^T\dot{R}={\mathrm{\Omega }}^{\wedge }.$

From this, we can obtain the kinematics equation of a rigid body based on SO(3):

where $R$ is the direction cosine matrix, with the corresponding Euler angles $\mathrm{\Theta }=\left[\begin{array}{c}\phi \\ \theta \\ \psi \end{array}\right]$, and $\mathrm{\Omega }=\left[\begin{array}{c}p\\ q\\ r\end{array}\right]$ is the angular velocity.

Let the error matrix and error vector between attitude A $R_1\in \mathrm{S}\mathrm{O}\left(3\right)$ and attitude B $R_2\in \mathrm{S}\mathrm{O}\left(3\right)$ be:

The attitude tracking error function is defined as [13]:

3.1. Robustness

The classic derivative link utilizes the property of an inertial element to track input signals with a delay, thereby approximating differentiation through the formula [14]:

However, inherent to the classic derivative link is a noise amplification effect, which becomes increasingly severe as $\tau$ decreases, often overwhelming the differential signal itself. To mitigate or attenuate this noise amplification issue, an alternative approximation for differentiation is employed:

The transfer function corresponding to this formula is derived as:

An equivalent state-variable implementation is thus given by:

Upon discretization, this becomes:

If the time constants ${\tau }_1$, ${\tau }_2$ approach a constant $\tau$, defining $r=\frac{1}{\tau }$, Eq. (10) transforms into:

which exhibits favorable differentiation properties when the parameter $r$ is sufficiently large. Consequently, Eq. (11) modifies to:

To attain the differential signal via dynamics that track input signals most swiftly, denote the synthesis function for the fastest tracking discrete system as ‘ $\mathrm{f}\mathrm{h}\mathrm{a}\mathrm{n}(v_1-v,v_2,r,h_0)$’. Where $v_1$ is the actual value, $v$ is the desired value, $h_0$ is the filtering factor (larger $h_0$ leads to better filtering effect), $h$ is the step size (smaller $h$ yields better filtering effect), generally $h_0$ is slightly larger than $h$.

The $\mathrm{f}\mathrm{h}\mathrm{a}\mathrm{n}$ formula is given by:

where, $\begin{array}{c}fsg(x,d)=\frac{\text{sign}(x+d)-\text{sign}(x-d)}{2}\end{array}$.

The discrete-time TD is given by:

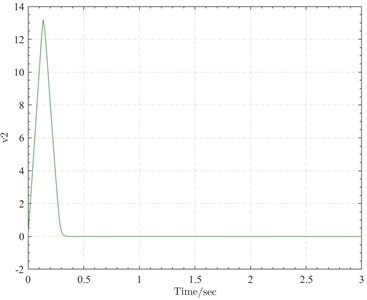
Fig. 1Variation of the first-order variable

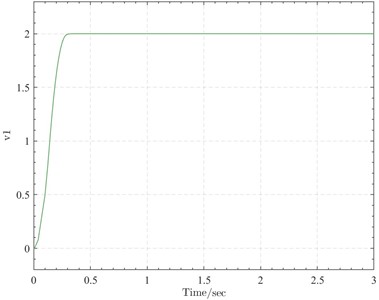
Fig. 2Variation of the second-order variable

Based on the classical second-order nonlinear TD, the TD design on SO(3) is given by:

where $R_d$ is the desired attitude.

3.2. Stability

Theorem Ⅰ: Concerning the system defined by $\left\{\begin{array}{c}{\dot{v}}_R=R{\mathrm{\Omega }}^{\wedge },\\ {\dot{v}}_{\mathrm{\Omega }}=fhan\left(e_R\left(v_R,R_d\right),v_{\mathrm{\Omega }},r,h_0\right).\end{array}\right.$

Proof: This theorem delineates a criterion for determining global asymptotic stability of nonlinear dynamic systems. It employs a positive definite function $V\left(z\right)$ (commonly referred to as the Lyapunov function), hinging upon Lyapunov’s stability theory – a pivotal branch in control theory utilized for analyzing and designing control system stability [15].

(1) Positive Definiteness: The function $V\left(x\right)$ tends to infinity as $x$ approaches infinity, implying that $V$ increases in all directions within the state space, particularly away from the origin. In other words, the larger the magnitude of the state variables, the greater the value of $V$. This suggests that if the system state deviates from the origin (the equilibrium point), the value of $V$ correspondingly increases, embodying the concept of positive definiteness.

(2) Negative Derivative of the Lyapunov Function: Along the system trajectories, the time derivative of $V\left(x\right)$, denoted $\dot{V\left(x\right)}$, is persistently negative (or non-positive in some cases, depending on the system and the analysis objective). This signifies that the system is “dissipating energy” at any non-equilibrium point, or equivalently, the system’s state consistently evolves toward a decrease in $V$. Crucial to system stability, this indicates that the system will not indefinitely maintain states distant from zero but instead converges to an equilibrium state.

(3) Uniqueness: Apart from the equilibrium point at $x=0$, there exists no other point for which $V\left(x\right)=0$. Thus, $x=0$ is the sole global minimum of $V\left(x\right)$. This assurance guarantees that all possible trajectories ultimately converge to this equilibrium point, as the system does not “halt” at any other point (reaching another local minimum).

By synthesizing these three conditions, it is deduced that the given system exhibits global asymptotic stability. Consequently, regardless of initial conditions (excluding the equilibrium point itself), the system's state progressively approaches and stabilizes at the origin $x=0$. This characteristic is vital in control system design, as it ensures the system's long-term stable behavior.

4.1. Large-angle maneuver

The desired attitude is set as ${\mathrm{\Theta }}_d=\left[\begin{array}{c}2\\ 1\\ 3\end{array}\right]$ rad. Under the action of the tracking differentiator, the Euler angle curve and the desired and output angle curves for roll, pitch, and yaw are shown in (a), (b), (c), and (d) of Fig. 3 respectively.

From the analysis of Fig. 3, it can be seen that initially, the roll angle $\phi$ and pitch angle $\theta$ slightly decrease, and then both increase to the desired values of ${\phi }_d=\text{2}$ rad and ${\theta }_d=\text{1}$ rad at approximately 0.4 seconds. This tracking approach appears to be “seeking the distant before the near”, but it is actually the fastest tracking method, which will be analyzed and demonstrated in the subsequent tracking error variation curve Fig. 5. The yaw angle $\psi$ starts from –2 rad and reaches $-\pi$ (i.e., $\pi$) at 0.2 seconds, and then attains the desired value of $\psi =$3 rad at approximately 0.4 seconds. Therefore, during large-angle maneuvers, the tracking differentiator can achieve attitude angle tracking control for the duct-type unmanned aerial vehicle.

Fig. 3Angle variation curves: a) Euler angle curve, b) desired and measured roll angle curves, c) desired and measured pitch angle curves, d) desired and measured yaw angle curves

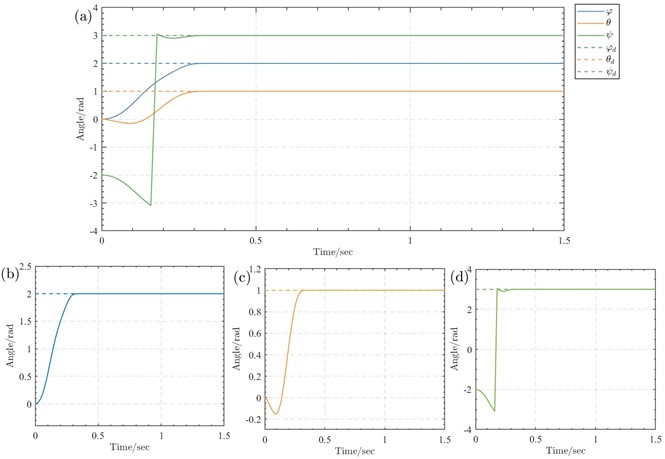
Fig. 4Angular velocity curves

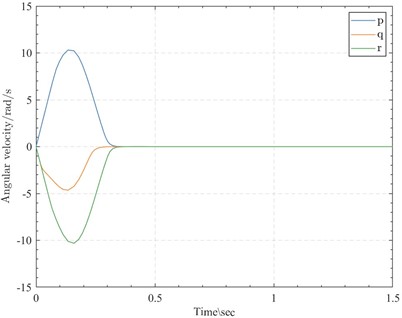
To reduce the tracking error to zero, the initial values of the angular velocities in all three directions were set to zero, and the dynamic variation plot is shown in Fig. 4. Around 0.3 seconds, the angular velocities in all three directions became zero again. Specifically, the roll angular velocity $p$ and pitch angular velocity $q$ both reached their extreme values of approximately 10.31 rad/s and –4.65 rad/s, respectively, at around 0.13 seconds, while the yaw angular velocity $r$ reached its minimum value of approximately –10.31 rad/s at around 0.16 seconds.

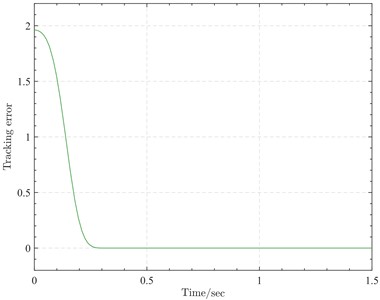
Fig. 5 shows the tracking error variation curve. The initial error was approximately 1.96, and the tracking error curve exhibited a smooth decreasing trend. At 0.3 seconds, the error decreased to 0.0004, which is nearly zero, and could be maintained within a small positive interval around zero. This explains the aforementioned “seeking the distant before the near” angle variation approach, which follows the shortest path to reach the desired attitude. In other words, the tracking differentiator can provide the shortest rotational path from the initial attitude to the target attitude.

Fig. 5Tracking error variation curve

4.2. Complex attitude tracking

The desired attitude was set as ${\mathrm{\Theta }}_d\left(t\right)=[-\mathrm{s}\mathrm{i}\mathrm{n}(t),\mathrm{1,2}\mathrm{s}\mathrm{i}\mathrm{n}(t\left)\right]$ rad. Under the action of the tracking differentiator, the Euler angle curve and the desired and output angle curves for roll, pitch, and yaw are shown in (a), (b), (c), and (d) of Fig. 6, respectively.

Fig. 6Angle variation curves: a) Euler angle curve, b) desired and measured roll angle curves, c) desired and measured pitch angle curves, d) desired and measured yaw angle curves

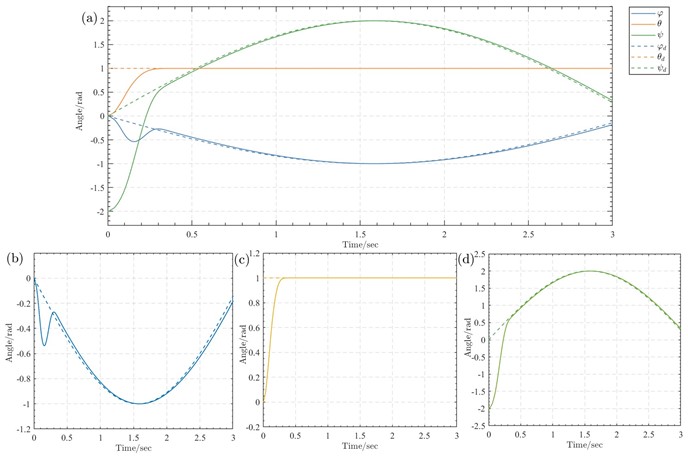
From the analysis of Fig. 6, it can be seen that initially, the roll angle $\phi$ first decreased and reached –0.54 rad at 0.15 seconds before increasing, and essentially attained the desired value ${\phi }_d$ after 0.3 seconds. The pitch angle $\theta$ steadily increased within the first 0.3 seconds and essentially reached the desired value of ${\theta }_d=\text{1}$ rad after 0.3 seconds. The yaw angle $\psi$ was initially set to –2 rad, steadily increased within the first 0.3 seconds, and essentially attained the desired value ${\psi }_d$ after 0.3 seconds. Therefore, during complex attitude tracking, the tracking differentiator could achieve attitude angle tracking control for the unmanned aerial vehicle.

Fig. 7Angular velocity curves

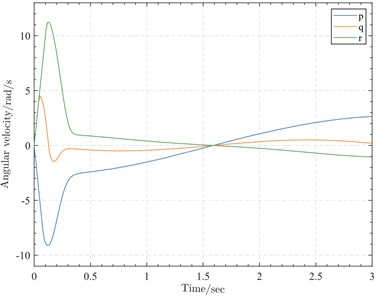
The dynamic variations of the angular velocities in three directions are depicted in Fig. 7. Around 0.3 seconds, the trends of the angular velocities in all three directions tend to stabilize. Specifically, the roll angular velocity $p$ reaches its minimum value of approximately –9.1 rad/s at around 0.13 seconds, followed by a sharp increase to its maximum value of 0.37 rad/s at 0.35 seconds, and subsequently exhibits a steady increase. The pitch angular velocity $q$ reaches its maximum value of approximately 4.51 rad/s at around 0.05 seconds, then rapidly decreases to its minimum value of –1.47 rad/s at 0.17 seconds, followed by a sharp increase to its maximum value of –0.29 rad/s at 0.31 seconds, and finally tends to flatten out. The yaw angular velocity $r$ reaches its maximum value of approximately 11.3 rad/s at around 0.13 seconds, then rapidly decreases to its minimum value of 0.98 rad/s at 0.37 seconds, and subsequently exhibits a steady decrease.

Fig. 8Tracking error variation curve

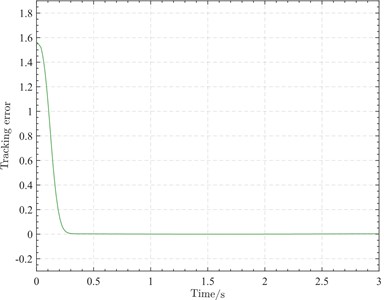
Fig. 8 illustrates the tracking error variation under complex attitude tracking. The initial error is approximately 1.55, similar to the case of large-angle maneuver. The tracking error curve exhibits a smooth decreasing trend, with the error decreasing to 0.004 at 0.3 seconds, which is nearly zero, and can be maintained within a small positive interval around zero. Therefore, this result further confirms that the tracking differentiator can provide the shortest rotational path from the initial attitude to the target attitude under more robust conditions.