Abstract
The article presents the results of the natural frequencies of vibrations of the span structure during the express-diagnostics, to excite the process of vibrations of the structure the pulse impact of the concentrated load of small mass is applied in the middle of the span structure (the method of small pulse impacts – “human jump”). The analysis of the obtained data, allowed to establish the parameters of free vibrations of unloaded span structures, the predominant frequencies on the graph of spectral density of dispersion are identical, regardless of the number of jumps, that is, the frequency of impact, if the time between jumps corresponds to the complete damping of vibrations. Of practical interest in the assessment of the technical condition is a quantitative assessment of the change in the natural frequency of vibration of girder metal and reinforced concrete spans depending on the presence of defects accumulated during the operation of the bridge. The obtained characteristics can serve as initial data, increasing the accuracy of calculations for calculations of artificial structures for seismic resistance, as well as in dynamic stability calculations for prospective loads and in the development of a model of the structure, the formation of algorithms of tasks to identify defects.
Highlights
- Transport structure subjected to dynamic effects from moving loads.
- The main elements of bridges that absorb dynamic effects.
- Distance between the extreme points of displacement along the axis of an element, measured by seismometers.
- A technique for detecting defects and internal damage in structural elements of bridges.
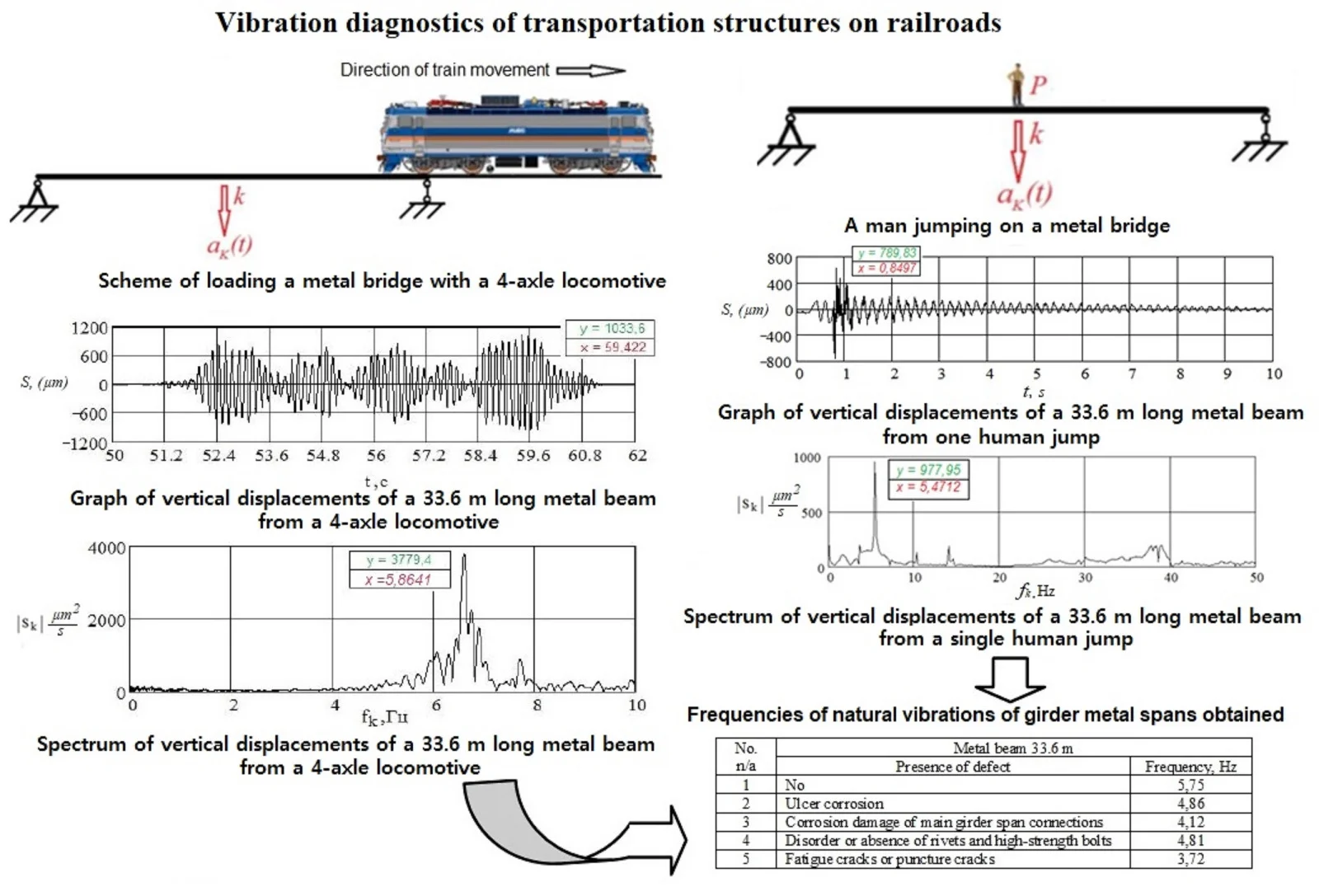
1. Introduction
The design standards of clause 1.48* [1] regulate the natural frequencies of vibration for girder sectional metal and steel reinforced concrete spans of railway bridges, as well as pedestrian and urban bridges. The natural frequencies of the span vibrations recorded under the passing load will be significantly different from the design frequencies due to the presence of a significant variable mass of rolling stock on the structure at that moment [2-4]. Taking into account that the linear mass of metal spans of old design standards is within 50-100 kN/m, and the distributed load from the currently circulating rolling stock may exceed 100 kN/m, it is not possible to record the true natural frequencies of vibration of structures under a moving train. Therefore, the natural frequencies of vibration of structures are determined either by the “tails” of experimental vibrograms (oscillograms) after the load leaves the span, or, if it is necessary to carry out express diagnostics, an impulse impact of a concentrated load of small mass in the middle of the span is applied to excite the process of vibration of the structure (the method of small impulse impacts – “human jump”) [5].
The obtained characteristics can serve as input data that increase the accuracy of calculations for calculations of artificial structures for earthquake resistance, as well as in dynamic stability calculations for prospective loads and in the development of a model of the structure, the formation of algorithms for tasks to identify defects [6-10]. The obtained results of the author’s full-scale experimental scientific research have been published in the editions of peer-reviewed journals and in the proceedings of the International Scientific and Practical Conferences, in which the author personally participated and made presentations, published in Russia and Kazakhstan [4, 5, 11]. When conducting research, special attention was paid to the functions of vibration velocities, vibration displacements and vibration accelerations, as well as amplitude Fourier spectra [2, 12-17].
The methods of determining the natural frequencies of vibration of girder spans based on the “tails” of experimental vibrograms and small impulse impacts have been tested and are widely used in the practice of diagnostics of railway bridges by specialists of JSC TsNIIS [18], MADI [19] and SGUPS [20, 21].
2. Materials and methods of research
2.1. Materials and equipment
Vibrodynamic software and hardware complex (VPAK) is designed for dynamic testing of structures of artificial structures and serves for measuring dynamic characteristics of bridges under the impact of rolling stock, as well as small impulse impact (Fig. 1). The VPAC consists of: protected industrial laptop with software for data processing and visualization “DYNAMIK” (1); rechargeable battery with capacity of 1200 mAh (2); measuring voltage converter E-14-440D (3), designed to measure DC and AC voltage, for input, output and processing of analog and digital information in measuring devices and systems; connecting shielded cables 50 m long (4); set of seismometers (5) EP-300-compact (three-component seismometers with a liquid calming device) for determination of natural vibration frequencies and amplitude-frequency characteristics (AFC) of bridge spans in vertical (Z), horizontal-transverse (Y) and horizontal-longitudinal (N) directions.
Fig. 1General view of the vibrodynamic hardware-software complex

2.2. Methods of investigation of dynamic effects on girder spans of railway bridges
The objects of research were railroad bridges: metal girder bridges 36.6 m (Fig. 2), type of bridge deck – on wooden bars; reinforced concrete girder bridges 6+2×9.4+6 m, type of bridge deck – on crushed stone ballast.
2.3. Results of determination of dynamic characteristics of girder spans of railway bridges
Of particular interest in this research are both functions and amplitude Fourier spectra [17, 18] obtained from the impact on the bridge span structure as a result of one person jumping in the middle of the span.
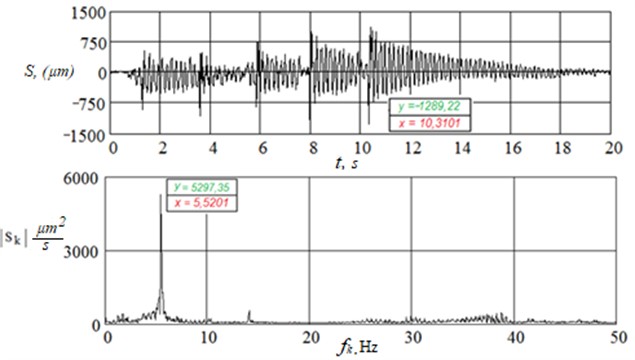
As an example, the amplitude-time and amplitude-frequency dependences of vibrations of the girder metal span of the railroad bridge with a span of 33.6 m across the Sarybulak River, obtained under a small impulse impact from a single jump of a person weighing 80-90 kg in Fig. 3, from five jumps in Fig. 4, where S – displacement, µm; t – time, s; |Sk| – modulus of the spectral density of displacement, (µm)/s; fk– frequency, Hz [4].
Fig. 2Scheme of the metal bridge span and location of seismometers of the Sarybulak River: 1 and 2 – seismometers installed in the middle of the span; P – load from one person (impulse – jumping)
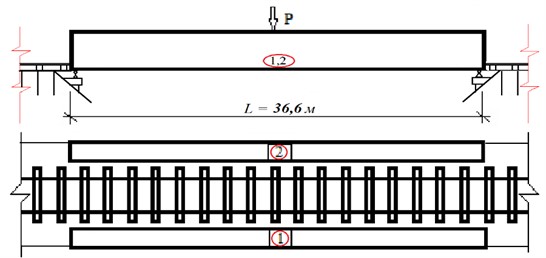
Fig. 3Vertical displacement graph and vertical displacement spectrum in the middle of a 33.6 m metal beam span from a single human jump
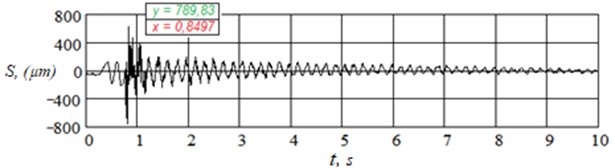
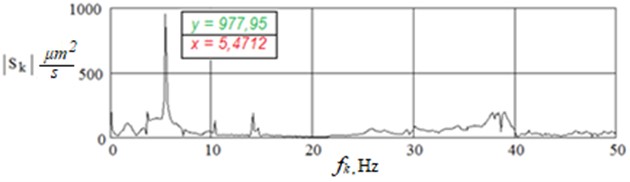
Fig. 4Vertical displacement graph and vertical displacement spectrum in the middle of a 33.6 m metal beam span from five human jumps
2.4. Determination of the relative damping coefficient of metal and reinforced concrete girder bridge spans
In dynamic calculations, the shapes of spectral curves in the region of resonances allow us to determine such a characteristic of the structure as the modal relative damping coefficient. Recall that the relative damping coefficient is equal to the ratio of the real damping to the critical damping.
At present, the relative damping coefficient, rather than the logarithmic decrement of oscillations, is regulated and used in the normative documents on the calculation of structures for seismic effects.
The relative damping coefficient ξ when performing experimental work is determined by the width of the spectral resonance curve at the points of half energy (Fig. 5) using the formula:
Fig. 5Example of resonance curve with indication of points of half energy
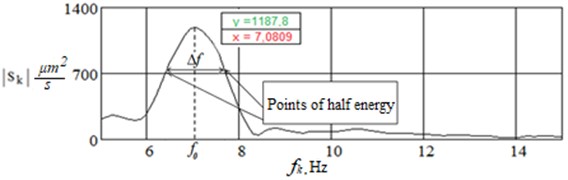
This parameter is the modal damping coefficient corresponding to a given frequency and shape of natural oscillations. The frequency interval between half-energy points is often referred to as the width of the system spectrum. The width of the interval between half-energy points determines the property of the system to dissipate energy during oscillations. An increased width of the interval between half-energy points can indicate the presence of cracks in concrete, although this is not the only reason [22].
For example, the relative coefficient for reinforced concrete beams without cracks is 3 %, while in the presence of cracks it is 5-7 %. For a metal beam, a wide spectrum in the resonant frequency region of 7 % was obtained, which indicates that energy dissipation occurs not only in the span structure (in the metal and in the connections of the beam elements), but also in the interaction with the supports and the track structure: ξ=Δf2∙f0=1,052∙7,08=0,07. More often than not, ξ for steel girder vibrations does not exceed 3 % [23].
2.5. Analysis of natural frequencies of vibrations of girder spans under impulse impact of small masses
The experimental data obtained from the testing of the 36.6 m span metal girder is presented in Table 1.
Table 1Experimental data of natural frequencies of metal beam 36.6 m
Metal beam 36.6 m | The number of jumps of one person | ||||
One | Two | Three | Five | ||
Peak values of vibration displacements, µm | Beam No.1 (left) | –762 | –1145 | –1814 | –1289 |
Beam No. 2 (right) | 789 | 5281 | 165 | 366 | |
Predominant frequency on the spectral density plot, Hz | Beam No.1 (left) | 5,47 | 5,52 | 5,47 | 5,52 |
Beam No. 2 (right) | 5,47 | 5,47 | 5,47 | 5,52 | |
As a result of the analysis of the conducted tests it was revealed that under the impact of small masses (human jumps) on the girder metal span structure of the bridge over the Sarybulak river, the frequencies of natural vibrations of this span structure are in the range fm= 5,47-5,52 Hz. These frequencies determine the periods of natural vibrations of metal girder bridge spans, which are standardized by SP [24].
Experimental data obtained during testing of 6 m and 9.4 m reinforced concrete girder spans are given in Table 2.
Table 2Experimental data of natural frequencies of reinforced concrete beams 6 m and 9.4 m
Reinforced concrete beam 6 m | The number of jumps of one person | |||
One | Three | Five | ||
Peak values of vibration displacements, µm | Seismic receiver No. 1 | 486 | –2121 | 1324 |
Seismic receiver No.4 | 3881 | –461 | 1015 | |
Predominant frequency on the spectral density plot, Hz | Seismic receiver No. 1 | 13,59 | 14,19 | 13,39 |
Seismic receiver No. 4 | 15,06 | 13,29 | 14,08 | |
Reinforced concrete beam 9.4 m | The number of jumps of one person | |||
One | Three | Five | ||
Peak values of vibration displacements, µm | Seismic receiver No. 2 | –1730 | –3668 | 2995 |
Seismic receiver No. 3 | –3491 | –1248 | –4198 | |
Predominant frequency on the spectral density plot, Hz | Seismic receiver No. 2 | 14,86 | 15,05 | 14,76 |
Seismic receiver No. 3 | 14,08 | 14,08 | 14,08 | |
As a result of the analysis of the conducted tests, it was determined that under the influence of small masses on the reinforced concrete girder bridge spans, the natural frequencies were in the range: for 6 m girders frc=13,29-15,06 Hz, and for 9.4 m beams frc=14,08-15,05 Hz. These frequencies determine, first of all, the period of natural vibrations of a reinforced concrete girder bridge span.
The analysis of the experimental data characterizing the response of the structure to the impact of small masses (human jumps) allowed us to establish the parameters of free vibrations of unloaded spans. The predominant frequencies on the dispersion spectral density plot are identical regardless of the number of jumps, i.e. the frequency of impact, if the time between jumps corresponds to the complete damping of vibrations.
The analysis of experimental data characterizing the response of bridge structures allowed us to establish the parameters of natural vibrations of unloaded spans [25-27].
According to the natural vibrations of girder spans of railroad bridges from a small impulse impact and from the impact of any passing trains, it can be concluded that the frequencies of natural vibrations of structures are close in numerical values. The same situation is observed when determining the relative damping coefficient. Discrepancies between quantitative values do not exceed 5 % for natural frequencies and 7 % for the relative damping coefficient, which is quite acceptable for this kind of research. The results of vibrodiagnostics based on measurements from small pulse impact are close in values to the results obtained in vibrodiagnostics from the impact of any moving load.
Vibrograms of natural vibrations are recorded using special highly sensitive seismometers, which are part of the measuring and computing complex for dynamic testing of structures, installed in the middle of the span on the upper (or lower) chord of one of the metal beams. Decrease of natural frequencies of vibrations can serve as an indicator of technical condition of a structure, which is confirmed by in-situ measurements of vibration parameters of more than 28 artificial structures.
Table 3 shows the results of measurements of natural frequencies of vibrations of metal girders of span structures obtained experimentally. The frequencies are determined for defect-free and defective girder spans.
Further, the results of measurements of natural frequencies for defect-free and defective girder metal and reinforced concrete spans of railroad bridges are given (Table 4), frequencies were determined for two values, before defect elimination – increase of ballast layer under sleeper 0.65 m and after, at normal thickness of ballast under sleeper 0.25 m.
Of practical interest in the assessment of the technical condition is the quantitative assessment of the change in the natural frequency of vibration of reinforced concrete and metal spans depending on the presence of defects accumulated during the operation of the bridge.
Table 3Frequencies of natural vibrations of girder metal spans obtained experimentally
No. n/a | Metal beam 33.6 m | |
Presence of defect | Frequency, Hz | |
1 | No | 5,75 |
2 | Ulcer corrosion | 4,86 |
3 | Corrosion damage of main girder span connections | 4,12 |
4 | Disorder or absence of rivets and high-strength bolts | 4,81 |
5 | Fatigue cracks or puncture cracks | 3,72 |
Table 4Experimentally obtained frequencies of natural vibrations of metal and reinforced concrete beams
Metal beam | Defect-free spanning structure | Defective spanning structure (cracks-penetrations) |
First natural frequency, Hz / Period, s | ||
33.6 m | 5,52 / 0,181 | 3,72 / 0,269 |
Reinforced concrete beam | Ballast thickness 0.25 m (Normal) | Ballast thickness 0.65 m (Defect) |
First natural frequency, Hz / Period, s | ||
6.0 m | 19,16 / 0,052 | 13,29 / 0,075 |
9.4 m | 15,05 / 0,066 | 11,39 / 0,088 |
3. Conclusions
The obtained characteristics of vibrations of the system “SMALL IMPULSE (PURPLE) – PATH – MOST” can serve as initial data for calibration of the structure model and for compilation of algorithms for damage detection tasks.
From the analysis of in-situ measurements of vibration processes of girder spans it follows that the width of spectra at the points of half energy of the spectral curve in the region of resonances should be used to assess the condition of spans. By comparing the width of the obtained spectra with the spectra of new undamaged spans, it is possible to estimate the technical condition of structural elements.
The technical condition of cut metal and reinforced concrete girders is also characterized by the relative damping coefficient, which increases in the presence of defects affecting the bearing capacity of the structure.
References
-
“Bridges and Pipes,” SP RK 3. 03-112-2013.
-
M. R. Kaloop and J. W. Hu, “Dynamic performance analysis of the towers of a long-span bridge based on gps monitoring technique,” Journal of Sensors, Vol. 2016, pp. 1–14, Jan. 2016, https://doi.org/10.1155/2016/7494817
-
A. N. Yashnov and A. V. Slyusar, Improving the diagnostic technique of reinforced concrete spans based on the results of their dynamic performance analysis. Society of Reinforced Concrete Manufacturers of Siberia and the Urals, Novosibirsk, 2005.
-
“Mechanical Vibration and Shock Measurements,” Bruel and Kjaer, 1890.
-
A. A. Parimbetov and I. S. Bondar, “Experimental studies of the impact of small masses on the metal beam of the railway bridge,” in Transport in the XXI Century: Status and Prospects, 2016.
-
I. S. Bondar, M. Y. Kvashnin, D. T. Aldekeeva, and A. A. Zaitsev, “Instrumental diagnostics of metal railroad bridges,” in 15th International Scientific and Technical Conference. Modern Problems of Design, Construction and Operation of the Railroad Track, 2018.
-
M. Y. Kvashnin, I. S. Bondar, and D. T. Aldekeyeva, “Identification of defects in reinforced concrete girder bridge spans,” in 7th International Scientific and Practical Conference "Automobile roads and transport engineering: problems and prospects of development", 2019.
-
N. Bonessio, G. Lomiento, and G. Benzoni, “Damage identification procedure for seismically isolated bridges,” Structural Control and Health Monitoring, Vol. 19, No. 5, pp. 565–578, Mar. 2011, https://doi.org/10.1002/stc.448
-
Y. Yang, Q. Li, and B. Yan, “Specifications and applications of the technical code for monitoring of building and bridge structures in China,” Advances in Mechanical Engineering, Vol. 9, No. 1, p. 168781401668427, Jan. 2017, https://doi.org/10.1177/1687814016684272
-
A. Belyi, E. Karapetov, and Y. Efimenko, “Structural health and geotechnical monitoring during transport objects construction and maintenance (Saint-Petersburg example),” Procedia Engineering, Vol. 189, pp. 145–151, Jan. 2017, https://doi.org/10.1016/j.proeng.2017.05.024
-
Kvashnin, M. Ya., Bondar I. S., and A. M. Zhangabylova, “Monitoring of the impact of rolling stock on the girder spans of railway bridges,” in Transport Science and Innovation, 2015.
-
Y. V. Arkhipenko, “Methodology of calculation of dynamic impact of moving loads with bridges with application of program complexes of finite element analysis,” OAO TSNIIS, 2006.
-
R. Menley, Analysis and Processing of Vibration Records. Moscow, 1972.
-
N. K. Snitko, Dynamics of Structures. Gosstroyizdat, 1960.
-
V. V. Krylov, “Effects of track properties on ground vibrations/generated by high-speed trains,” Acta Acustica, Vol. 84, No. 1, pp. 78–90, 1998.
-
N. M. Kvashnin, “Investigation of mechanical vibrations of the railway track,” Almaty, 2010.
-
M. Y. Kvashnin, N. M. Kvashnin, and I. S. Bondar, “Wavelet analysis in vibroacoustic control method,” The World of Transport, Vol. 6, No. 55, pp. 78–84, 2014.
-
“Inspection and acceptance tests of the road overpass over the railroad tracks of the Moscow railroad near Bolshevo station in Korolev,” OAO TsNIIS, 2005.
-
M. L. Khazanov, “Processing of the results of dynamic tests of bridge structures by the program "Spektr",” Central Research Institute of Structural Engineering, 2002.
-
D. N. Tsvetkov, “Estimation of the technical condition of the steel-reinforced concrete spans of the railroad bridges by the dynamic parameters,” Novosibirsk, 2010.
-
S. A. Bokarev, A. N. Yashnov, I. I. Snezhkov, and A. V. Slyusar, “Small-size automated systems for the ISOS diagnostics,” Railroad track and track facilities, Vol. 9, pp. 25–26, 2007.
-
E. N. Kurbatskiy, “Use of the vibration theorem for an estimation of the vibration levels of an elastic half-space surface from a point source located inside the half-space,” (in Russian), Vestnik of MIIT, 2004.
-
E. N. Kurbatsky, I. S. Bondar, and M. Y. Kvashnin, “Research of the girder bridges response to the train impact,” The World of Transport, Vol. 13, No. 3, pp. 58–71, 2015.
-
“Bridges and pipes,” Moscow, 122. SPP 35.13330.2011, 2011.
-
S. S. Abdullayev, I. S. Bondar, G. B. Bakyt, G. K. Ashirbayev, A. M. Budiukin, and Y. Y. Baubekov, “Interaction of frame structures with rolling stock,” Series of Geology and Technical Sciences, Vol. 445, No. 1, pp. 22–28, Feb. 2021, https://doi.org/10.32014/2021.2518-170x.3
-
A. Akbayeva et al., “Development of safety methods on artificial structures of railway lines,” Eastern-European Journal of Enterprise Technologies, Vol. 6, No. 1 (120), pp. 43–52, Dec. 2022, https://doi.org/10.15587/1729-4061.2022.269964
-
S. S. Abdullayev, G. B. Bakyt, M. N. Aikumbekov, I. S. Bondar, and Y. T. Auyesbayev, “Determination of natural modes of railway overpasses,” Journal of Applied Research and Technology, Vol. 19, No. 1, pp. 1–10, Mar. 2021, https://doi.org/10.22201/icat.24486736e.2021.19.1.1487
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.

