A mathematical model and microcontroller-based method for measuring dielectric permittivity and discharge characteristics with Arduino ATmega 328: a case study in a physics laboratory

Putra, Valentinus Galih Vidia; Ngadiyono

doi:10.21595/mme.2023.23695

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 23 November 2023

Check for updates

A mathematical model and microcontroller-based method for measuring dielectric permittivity and discharge characteristics with Arduino ATmega 328: a case study in a physics laboratory

Valentinus Galih Vidia Putra¹

Ngadiyono²

¹Basic and Applied Science Research Group in Theoretical and Plasma Physics, Politeknik STTT Bandung, Bandung, Indonesia

²Department of Textile Engineering, Politeknik STTT Bandung, Bandung, Indonesia

Corresponding Author:

Valentinus Galih Vidia Putra

Cite the article Download PDF

Downloads 226

Abstract

A microcontroller-based measuring instrument and a new mathematical model are used to investigate capacitor permittivity and dielectric materials' charge-discharge characteristics. In this study, a prototype capacitive permittivity measurement apparatus for dielectric materials was carefully developed using an Arduino microcontroller, a resistor, and a capacitor. The experimental setup comprises a capacitor-resistor circuit, wherein a 5-volt power supply sourced from the microcontroller interfaces with a computer. During the charging process, a comprehensive evaluation of model-data alignment was performed, yielding values of 0.54252156, 0.9951, and 111.2508701 for the sum of squares error (SSE), the coefficient of determination (R-squared), and the sum of squares total (SST), respectively. Similarly, the analysis extended to the discharging process, unveiling values of 5.10174756, 0.962805684, and 137.1647082 for SSE, R-squared, and SST, respectively. These findings confirm the accuracy of the microcontroller that was programmed by incorporating a model in precisely measuring the relative permittivity of dielectric materials and capacitance values, with an R-squared value above 0.95 following capacitor literature benchmarks. The novelty of this study is that this configuration enabled the precise assessment of both permittivity and the charge-discharge characteristics of the dielectric materials within the capacitor. This methodology made it possible to accurately measure the permittivity and charge-discharge characteristics of dielectric materials within a capacitor. The scientific significance of this research lies in its ability to provide a carefully developed instrument capable of investigating the permittivity of dielectric materials and capacitor capacitance measurements. Scholars, international engineering communities, and academics can use this technological breakthrough to advance research into dielectric material properties and capacitor characteristics.

A mathematical model and microcontroller-based method for measuring dielectric permittivity and discharge characteristics with Arduino ATmega 328: a case study in a physics laboratory

Highlights

Accurately measure the permittivity and charge-discharge characteristics of dielectric materials within a capacitor
Rigorous analysis
Compare the model with experiment
A mathematical model and microcontroller-based method

1. Introduction

Measuring the permittivity and dielectric properties of materials and the charge-discharge process in capacitors is a crucial aspect of electrical engineering and material science [1]. Several scholars have applied physics principles to advance various aspects of electronics [2, 3]. According to some researchers, understanding materials’ permittivity and dielectric properties is crucial for designing electronic devices [4]-[10]. Capacitors store electrical energy, and their performance depends on the dielectric material between the plates. Engineers can choose the most suitable dielectric material by accurately measuring permittivity and optimize the capacitor's efficiency and performance [11]-[15]. In industrial applications, it is essential to ensure the consistency and quality of dielectric materials used in capacitors. Accurate measurement tools and models help quality control by verifying that the dielectric properties meet the required specifications. This ensures capacitors operate reliably and meet safety standards [16]-[18]. Permittivity and dielectric measurements also play a crucial role in material science. Researchers use these measurements to understand the electrical properties of various materials, not just for capacitors but also for applications in sensors, insulators, and semiconductors [17, 18]. For instance, Allagui, Elwakil, Fouda, and Radwan [1] have extensively explored the integration of physics in supercapacitors as reservoirs of stored energy. Arshad, Khan, Alam, Tasnim, Gunawan, Ahmad, and Nataraj [2] developed a system for monitoring senior citizen activity levels using capacitive sensing technology. Mita and Boufaida [3] have devised innovative capacitor circuits to optimize energy consumption. Dean, Bell, and Baty pioneered the innovative use of capacitance enhancement techniques [4]. Yang and Chenming [5] focused on quantifying capacitance in thin dielectrics characterized by elevated leakage. A novel microcontroller-based approach to capacitance measurement has been developed by Putra, Wijayono, Purnomosari, Ngadiono, and Irwan [6]. Researchers have extensively documented a wide range of research encompassing the application of microcontrollers for measuring physical attributes, specifically capacitance [7]-[18]. Permittivity, a fundamental parameter in electromagnetism that describes electric polarizability, has far-reaching implications. Higher permittivity materials exhibit a higher capacity for polarization in response to an applied electric field, denoted as E, resulting in the accumulation of increased energy within the electric field. The representation of permittivity typically includes the relative permittivity, absolute permittivity, and ratio relative to the vacuum permittivity, all of which serve as crucial descriptors in the permittivity characterization [19]. Measurement of permittivity and dielectric properties of materials, such as for the fabrication of electromagnetic shielding materials, is critical in electrical engineering and material science. [20]. Recognizing the critical role of permittivity in determining the capacitance of a capacitor within the context of electrostatics, Putra, Ngadiono, Wijayono, and Purnomosari [6], as well as Westerlund & Ekstam [7] demonstrated the indispensable importance of permittivity. Their research clearly showed the utility of physics in quantifying the capacitance of various materials using microcontrollers. It is worth noting that while their investigations accurately characterized capacitance during the charging and discharging processes, a thorough analysis of permittivity calculation for the capacitor materials was left out of their discussion. In this regard, an equation with more detailed analysis and validation of the model is required to study the characteristics of a dielectric material and the charge-discharge processes. This study aims to develop a microcontroller-based measuring instrument and a new mathematical model for studying capacitor permittivity and the charge-discharge characteristics of dielectric materials. The study has significant scholarly implications, providing a novel tool for studying dielectric material permittivity and capacitor capacitance. This innovative tool, designed to aid researchers and academics, enables sophisticated research within these comprehensive areas.

2. Research methods

2.1. Materials

A capacitor (330 μF), a resistor (51 kΩ), a DC source voltage (5 volts), several cables, and a project board comprised the experimental apparatus. These parts were purchased in Bandung, Indonesia's traditional market. The dielectric material under consideration was an ideal cylindrical capacitor with an unspecified dielectric type and permittivity value. We determined the permittivity of the dielectric material for the ideal capacitor using the charge-discharge resistor-capacitor (RC) method and a 5 V Arduino source voltage.

2.2. Instrumentations

The power supply connected the microcontroller, the capacitor-resistor circuit, and the computer. A capacitor-resistor circuit interfaced with a microcontroller ATmega 328 was used in this study performed at Politeknik STTT Bandung, Indonesia. This study investigated the permittivity and capacitance of dielectric materials.

2.3. Methods

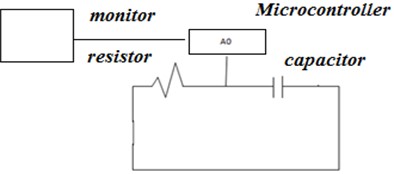
The experiment scheme is depicted in Fig. 1 and Fig. 2. In Fig. 3, it shows the capacitance measurement using the Arduino ATmega 328 microcontroller.

Fig. 1Charging scheme of the cylinder capacitor

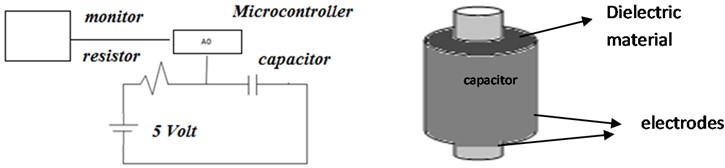
Fig. 2Discharging scheme of the capacitor

The following are the procedures for measuring capacitance and permittivity: On a computer, an Arduino program was created and transferred to the Arduino ATmega 328 microcontroller on the project board, with resistors and capacitors configured as shown in Fig. 1 and Fig. 2. The computer was connected to the microcontroller, and the program was uploaded to it. After that, the capacitor was gradually charged up to a maximum voltage of 5 volts or until it stabilized. Following that, discharging was done from 5 volts to 0 volts or until steadiness was achieved. Microsoft Office Excel was used to compare experimental and theoretical results.

Fig. 3Measuring capacitance using a microcontroller

3. Mathematical model

A new mathematical equation was constructed to quantify the capacitance and permittivity of dielectric materials. Notably, this model was constrained because the dielectric substance was located between two conducting plates that served as positive and negative electrodes. The plates, which had a cylindrical shape, kept a specific distance from the dielectric material. The dielectric material then aligned with the two electrodes. In this experimental setup, an RC circuit was constructed, comprising a 330 μF capacitance in series with a 51.000 ohms resistor powered by a 5-volt input voltage source. A microcontroller device facilitated the charging and discharging of capacitors for obtaining permittivity and capacitance measurements. The capacitor voltage was monitored experimentally every two seconds, commencing from the initial voltage of 0 and increasing to 5 volts during the charging phase. This voltage data was then compared with theoretical predictions to determine capacitance and relative permittivity. The same procedure was repeated during the capacitor discharge phase. The measured voltage during the closed-circuit charging operation of the capacitor can be expressed as Eq. (1):

1

V = \frac{Q}{C} = V_{s} (1 - e^{- \frac{t}{R C}}),

where $V$ represents the capacitor voltage, $Q$ is the capacitor charge, $C$ represents capacitance, $V_{s}$ is the microcontroller source voltage, $t$ is time, and $R$ is resistance. Eq. (2) can be used to calculate the voltage for the capacitor discharge process:

2

V = V_{s} e^{t / R C} .

To determine the voltage theoretically, we can use Eq. (3):

3

β = \frac{1}{R C},

where $β$ is a constant value determined by the capacitor and resistor values using the microcontroller and resistor-capacitor circuit. We control five-volt DC for the supply voltage and use Eq. (3) to calculate the capacitor voltage, V, as shown in Eq. (4):

4

V_{c} = 5 (1 - e^{- t β}) .

It can be used $R^{2}$ to know the accuracy value of our prediction from the curve using Eq. (5) as shown below:

5

R^{2} = 1 - \frac{S S E}{S S T} .

SSE represents the sum of squares error, $R^{2}$ is the coefficient of determination, and the sum of squares total for the SST. The capacitance, $C$ , can be measured using Eq. (6):

6

C = \frac{1}{R β} .

In the cylinder capacitor (Fig. 1), it has been found that for the diameter of the inner cylinder of $r = a$ and the diameter of the outer cylinder of $b$ with height $L$ , volume charge density, $ρ$ , permittivity, $ε$ , and the electric field, $E$ , in the area $r < a$ can be written in Eqs. (7) to (8):

7

\int \bar{E} ∙ d \bar{s} = \int \frac{ρ}{ε} d V, \iint |E| \hat{r} ∙ |r d φ d z| \hat{r} = ∭_{0}^{r = r} \frac{ρ}{ε} r d r d φ d z,

8

E ε 2 π r L = ρ π r^{2} L .

Hence, we get Eq. (9):

9

E = \frac{ρ π r^{2} L}{ε 2 π r L} = \frac{ρ r^{2}}{ε 2 r} = \frac{ρ r}{2 ε} .

The electric field on $a < r < b$ can be written as Eq. (10) to (12):

10

\int \bar{E} ∙ d \bar{s} = \int \frac{ρ}{ε} d V, \iint |E| \hat{r} ∙ |r d φ d z| \hat{r} = ∭_{0}^{r = a} \frac{ρ}{ε} r d r d φ d z .

11

E ε 2 π r L = ρ π a^{2} L .

12

E = \frac{ρ π a^{2} L}{ε 2 π r L} = \frac{ρ a^{2}}{2 ε r} = \frac{Q a^{2}}{π a^{2} L 2 ε r} = \frac{Q}{2 π ε r L} .

The electric field, $E$ , on $r > b$ is shown in Eq. (13):

13

E = \frac{ρ a^{2}}{2 ε r} - \frac{ρ a^{2}}{2 ε r} = 0 .

The voltage and capacitance can be written as Eq. (16) and Eq. (18):

14

∆ φ = \int_{1}^{2} \bar{E} ∙ d \bar{r} = \frac{∭_{0}^{r = a} ρ r d r d φ d z}{C},

15

∆ φ = \int_{a}^{b} \bar{E} ∙ d \bar{r} = \frac{Q}{C},

16

∆ φ = \int_{a}^{b} \frac{Q}{2 π ε r L} d r = \frac{Q}{2 π ε L} \ln (\frac{b}{a}),

17

C = \frac{Q}{∆ φ} = \frac{2 π ε L}{\ln (\frac{b}{a})},

18

ε = \frac{C b \ln (\frac{b}{a})}{2 π b L}, ε = C \frac{b \ln (\frac{b}{a})}{2 π b L} = \frac{1}{R β} \frac{b \ln (\frac{b}{a})}{2 π b L},

with $d^{*} = b \ln (\frac{b}{a})$ , $b =$ 0.7 cm, $a =$ 0.5 cm, $L =$ 1.28 cm, and $A = 2 π b L$ is the area of the cylinder capacitor. The capacitance and dielectric permittivity values can be calculated using Eqs. (6) and (18).

4. Results and discussions

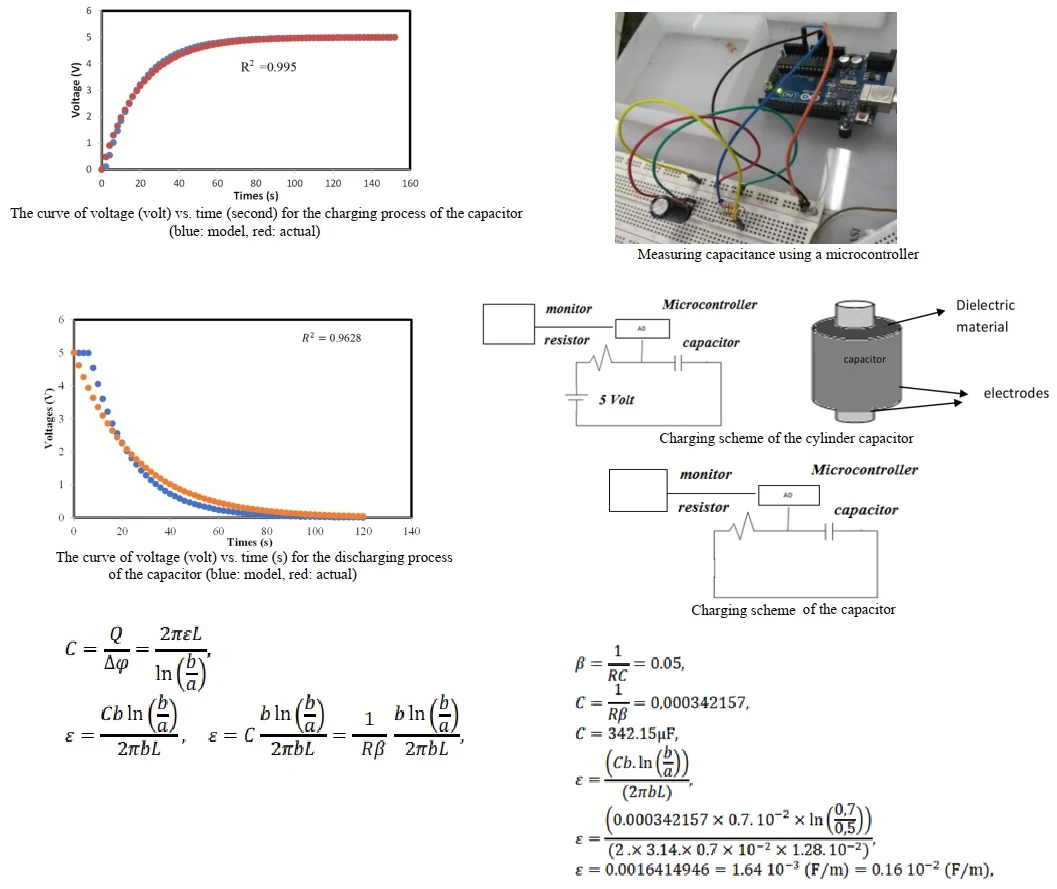
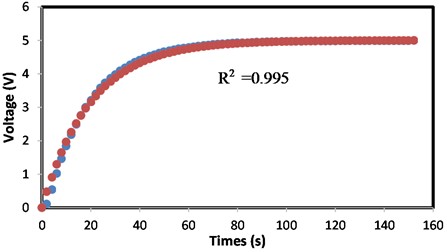
In this study, we have chosen a constant value determined by the capacitor and resistor values ( $β$ ) of 0.05 both for the charging and discharging process. After comparing the experimental results with the model using Eqs. (1), (4), (5), and (6), we demonstrated the relationship between experimental data and the model during the charging process of a 330 μF capacitor and a 51.000 ohms resistor. Fig. 4 depicts the fit level between the model and data during the charging process, with values for the sum of squares error (SSE), coefficient of determination (R-squared), and sum of squares total (SST) of 0.54252156, 0.9951, and 111.2508701, respectively. Using the model, we discovered that the charging process’s $R^{2}$ was 0.99512344. The curve's result is depicted in Fig. 4.

Fig. 4The curve of voltage (volt) vs. time (second) for the charging process of the capacitor (blue: model, red: actual)

Based on Fig. 4, the capacitance and dielectric permittivity of the material can be calculated. Eq. (6) can be used to calculate capacitance, $C$ , and Eq. (18) to calculate the permittivity of dielectric material, resulting in Eqs. (19) to (24):

19

β = \frac{1}{R C} = 0.05,

20

C = \frac{1}{R β} = 0,000342157,

21

C = 342.15 μ F,

22

ε = \frac{(C b . \ln (\frac{b}{a}))}{(2 π b L)},

23

ε = \frac{(0.000342157 \times 0.7 . 10^{- 2} \times \ln (\frac{0,7}{0,5}))}{(2 . \times 3.14 . \times 0.7 {\times 10}^{- 2} \times 1.28 {. 10}^{- 2})},

24

ε = 0.0016414946 = 1.64 1 0^{- 3} (F / m) = 0.16 1 0^{- 2} (F / m),

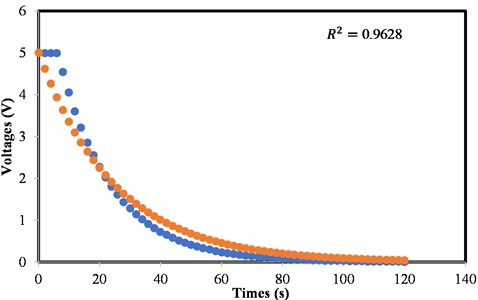
The dielectric permittivity value of the material is obtained by using Eq. (22) and then substituting the following values into the Equation: $b =$ 0.7 cm, $a =$ 0.5 cm, $L =$ 1.28 cm, and $A = 2 π b L$ is the area of the cylinder capacitor, and also $C =$ 342.157 μF. According to the model result in Eq. (21) and (24), the capacitance is 342.157 μF, while the actual capacitance result is 330 μF. According to the model, the material's dielectric permittivity is 0.16×10^-2 (F/m), which is generally in the range of dielectric values for the capacitor types used. We also showed the experimental data for the discharging process of capacitor 330 μF based on the experimental results. Furthermore, we measured the level of fit between the model and data in the testing process during the discharging process, and the values for the sum of squares error (SSE), the coefficient of determination (R-squared), and the sum of squares total (SST) were 5.10174756, 0.962805684, and 137.1647082, respectively. From Fig. 5, it can be shown that the $R^{2}$ of the discharging process of the capacitor is 0.9628.

Based on experimental results and models, the capacitance and permittivity values can be calculated using Eqs. (6) and (18). The capacitance measured in this experiment was 342.157 μF (the actual capacitance was 330 μF), and the capacitance permittivity was 0.0016414946 (F/m). $R^{2} >$ 0.95 was obtained for the charging and discharging process results, indicating that the correlation between predicted and experimental results is good. The capacitance values during this experiment's charging and discharging processes show the concordance between theory and experiment, as shown in Fig. 4 and Fig. 5. In this study, the dielectric materials within the capacitor were precisely assessed for permittivity as well as charge-discharge characteristics. This methodology made it possible to accurately measure the permittivity and charge-discharge characteristics of dielectric materials within a capacitor. In addition to providing a carefully developed instrument for measuring capacitor capacitance, this research is scientifically significant for its ability to investigate the permittivity of dielectric materials. The findings of this technological breakthrough can be used to advance research into dielectric material properties and capacitor characteristics by scholars, international engineering communities, and academics.

Fig. 5The curve of voltage (volt) vs. time (s) for the discharging process of the capacitor (blue: model, red: actual)

5. Conclusions

This study developed a method for accurately determining a capacitor's relative permittivity and capacitance value. A capacitor permittivity measurement prototype was created in this study using an Arduino microcontroller device. The capacitor permittivity was measured using a series of capacitor resistors with a 5-volt source from the microcontroller's voltage. A capacitor-resistor circuit with a 5-volt voltage source from a microcontroller connected to a computer device was used to measure the permittivity of the capacitor. It was found that the method used in this study was quite successful in measuring the capacitor's permittivity. It was concluded that microcontroller devices could accurately determine the relative permittivity of dielectric materials and capacitance values with the $R^{2}$ above 0.95 to the literature value on the capacitor. We measured the level of fit between the model and data in the experimental process during the charging process, with values of 0.54252156, 0.9951, and 111.2508701 for the sum of squares error (SSE), the coefficient of determination (R-squared), and the sum of squares total (SST), respectively. Furthermore, we also measured the level of fit between the model and data in the experimental process during the discharging process, and the values for the sum of squares error (SSE), the coefficient of determination (R-squared), and the sum of squares total (SST) were 5.10174756, 0.962805684, and 137.1647082, respectively. Based on our findings, we discovered that the capacitance and permittivity values could be calculated using Eqs. (6) and (18). The result of the capacitance in this experiment was 342.157 μF, while the actual capacitance was 330 μF, with the permittivity of dielectric materials of capacitance, ε, measured at 0.0016414946 (F/m).

References

A. Allagui, A. S. Elwakil, M. E. Fouda, and A. G. Radwan, “Capacitive behavior and stored energy in supercapacitors at power line frequencies,” Journal of Power Sources, Vol. 390, pp. 142–147, Jun. 2018, https://doi.org/10.1016/j.jpowsour.2018.04.035

Publisher
A. Arshad et al., “An activity monitoring system for senior citizens living independently using capacitive sensing technique,” in 2016 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), May 2016, https://doi.org/10.1109/i2mtc.2016.7520405

Publisher
K. Mita and M. Boufaida, “Ideal capacitor circuits and energy conservation,” American Journal of Physics, Vol. 67, No. 8, pp. 737–739, Aug. 1999, https://doi.org/10.1119/1.19363

Publisher
T. J. Dean, J. P. Bell, and A. J. B. Baty, “Soil moisture measurement by an improved capacitance technique, Part I. Sensor design and performance,” Journal of Hydrology, Vol. 93, No. 1-2, pp. 67–78, Aug. 1987, https://doi.org/10.1016/0022-1694(87)90194-6

Publisher
K. J. Yang and Chenming Hu, “MOS capacitance measurements for high-leakage thin dielectrics,” IEEE Transactions on Electron Devices, Vol. 46, No. 7, pp. 1500–1501, Jul. 1999, https://doi.org/10.1109/16.772500

Publisher
A. Wijayono and V. G. V. Putra, “Pengukuran Konstanta Dielektrik Udara Pada Perangkat Kapasitor Plat-Sejajar Berbasis Mikrokontroler Arduino Uno,” JIPFRI (Jurnal Inovasi Pendidikan Fisika dan Riset Ilmiah), Vol. 4, No. 1, pp. 13–26, May 2020, https://doi.org/10.30599/jipfri.v4i1.651

Publisher
S. Westerlund and L. Ekstam, “Capacitor theory,” IEEE Transactions on Dielectrics and Electrical Insulation, Vol. 1, No. 5, pp. 826–839, 1994, https://doi.org/10.1109/94.326654

Publisher
V. G. V. Putra and J. N. Mohamad, “Response surface methodology and artificial neural network modeling of work of adhesion on plasma-treated polyester-cotton-woven fabrics,” Journal of Adhesion Science and Technology, Vol. 37, No. 6, pp. 976–996, Mar. 2023, https://doi.org/10.1080/01694243.2022.2053349

Publisher
Y. A. Badamasi, “The working principle of an Arduino,” in 2014 11th International Conference on Electronics, Computer and Computation (ICECCO), Sep. 2014, https://doi.org/10.1109/icecco.2014.6997578

Publisher
T. Boltshauser, L. C. Azeredo, and H. Baltes, “High-sensitivity CMOS humidity sensors with the on-chip absolute capacitance measurement system,” Sensors and Actuators B: Chemical, Vol. 15, pp. 75–80, 1993, https://doi.org/10.1016/0925-4005(93)8503

Publisher
R. N. Dean and A. K. Rane, “A digital frequency-locked loop system for capacitance measurement,” IEEE Transactions on Instrumentation and Measurement, Vol. 62, No. 4, pp. 777–784, Apr. 2013, https://doi.org/10.1109/tim.2013.2240092

Publisher
F. Deflorian, L. Fedrizzi, S. Rossi, and P. L. Bonora, “Organic coating capacitance measurement by EIS: ideal and actual trends,” Electrochimica Acta, Vol. 44, No. 24, pp. 4243–4249, Jul. 1999, https://doi.org/10.1016/s0013-4686(99)00139-5

Publisher
L. B. Harris and J. Fiasson, “Vibrating capacitor measurement of surface charge,” Journal of Physics E: Scientific Instruments, Vol. 17, No. 9, pp. 788–792, Sep. 1984, https://doi.org/10.1088/0022-3735/17/9/016

Publisher
A. D. Mazzeo et al., “Paper‐Based, Capacitive Touch Pads,” Advanced Materials, Vol. 24, No. 21, pp. 2850–2856, Jun. 2012, https://doi.org/10.1002/adma.201200137

Publisher
H. Matsumoto, H. Shimizu, and K. Watanabe, “A switched-capacitor charge-balancing analog-to-digital converter and its application to capacitance measurement,” IEEE Transactions on Instrumentation and Measurement, Vol. IM-36, No. 4, pp. 873–878, Dec. 1987, https://doi.org/10.1109/tim.1987.6312573

Publisher
Pereira and N. S. A., “Measuring theRCtime constant with Arduino,” Physics Education, Vol. 51, No. 6, p. 065007, Nov. 2016, https://doi.org/10.1088/0031-9120/51/6/065007

Publisher
D. F. Williams and R. B. Marks, “Transmission line capacitance measurement,” IEEE Microwave and Guided Wave Letters, Vol. 1, No. 9, pp. 243–245, Sep. 1991, https://doi.org/10.1109/75.84601

Publisher
J. Xia, F. Chen, J. Li, and N. Tao, “Measurement of the quantum capacitance of graphene,” Nature Nanotechnology, Vol. 4, No. 8, pp. 505–509, Aug. 2009, https://doi.org/10.1038/nnano.2009.177

Publisher
D. Halliday, R. Resnick, and J. Walker, Fundamental of Physics-Extended, 5th. New York: John Wiley & Sons, 1997.

Search CrossRef
V. G. V. Putra, J. N. Mohamad, D. R. Arief, and Y. Yusuf, “Surface modification of polyester-cotton (TC 70%) fabric by corona discharged plasma with tip-cylinder electrode configuration-assisted coating carbon black conductive ink for electromagnetic shielding fabric,” Arab Journal of Basic and Applied Sciences, Vol. 28, No. 1, pp. 272–282, Jan. 2021, https://doi.org/10.1080/25765299.2021.1889116

Publisher

About this article

Received

10 October 2023

Accepted

31 October 2023

Published

23 November 2023

DOI

https://doi.org/10.21595/mme.2023.23695

Keywords

resistor

capacitor

permittivity

mathematical model

Acknowledgements

The study was funded by Politeknik STTT Bandung's Research and Community Service Division (UPPM) and the Republic of Indonesia's Ministry of Industry. The authors sincerely thank everyone who helped and contributed to this study. Their encouragement and motivation have influenced our decision to pursue this project.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Valentinus Galih Vidia Putra conducted the experiment and the calculations. Valentinus Galih Vidia Putra and Ngadiyono wrote and revised the manuscript. All authors agreed to the final version of this manuscript.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 05 18

Simulation of the measurement and control system of the electrostatic suspension inertial sensor

Jianhe Liu, Wenhao Huang, Yuqi Chen

Research article

2022 06 30

A comparative analysis of different approaches used for modelling and solving differential equations in Simulink/MATLAB

Pankaj Mohindru, Pooja Mohindru

Research article

2021 09 09

Development of a mathematical model of frequency controlled induction electric drive

Nazira Darimbaeva, Marat Mustafin, Nurgul Almuratova, Algazy Zhauyt

Research article

2021 01 18

The PWM rectifier with LCL filter direct power control based on power damping feedback

Qianqian Zhang, Bo Fan, Zhengxin Zhao, Shuaihui Gu

V. G. V. Putra and Ngadiyono, “A mathematical model and microcontroller-based method for measuring dielectric permittivity and discharge characteristics with Arduino ATmega 328: a case study in a physics laboratory,” Mathematical Models in Engineering, Vol. 9, No. 4, pp. 169–177, Nov. 2023, https://doi.org/10.21595/mme.2023.23695

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/mme.2023.23695
UR  - https://doi.org/10.21595/mme.2023.23695
TI  - A mathematical model and microcontroller-based method for measuring dielectric permittivity and discharge characteristics with Arduino ATmega 328: a case study in a physics laboratory
T2  - Mathematical Models in Engineering
AU  - Putra, Valentinus Galih Vidia
AU  - Ngadiyono
PY  - 2023
DA  - 2023/11/23
PB  - JVE International Ltd.
SP  - 169-177
VL  - 9
IS  - 4
SN  - 2351-5279
SN  - 2424-4627
ER  - 

Copy Ris

Copied to clipboard!

 @article{Putra_2023, title={A mathematical model and microcontroller-based method for measuring dielectric permittivity and discharge characteristics with Arduino ATmega 328: a case study in a physics laboratory}, volume={9}, ISSN={2424-4627}, url={https://doi.org/10.21595/mme.2023.23695}, DOI={10.21595/mme.2023.23695}, number={4}, journal={Mathematical Models in Engineering}, publisher={JVE International Ltd.}, author={Putra, Valentinus Galih Vidia and Ngadiyono}, year={2023}, month=nov, pages={169–177} }

Copy Bibtex

Copied to clipboard!

[1]V. G. V. Putra and Ngadiyono, “A mathematical model and microcontroller-based method for measuring dielectric permittivity and discharge characteristics with Arduino ATmega 328: a case study in a physics laboratory,” Mathematical Models in Engineering, vol. 9, no. 4, pp. 169–177, Nov. 2023, doi: 10.21595/mme.2023.23695.

Copy IEEE

Copied to clipboard!

Putra, Valentinus Galih Vidia, and Ngadiyono. “A Mathematical Model and Microcontroller-Based Method for Measuring Dielectric Permittivity and Discharge Characteristics with Arduino ATmega 328: A Case Study in a Physics Laboratory.” Mathematical Models in Engineering 9, no. 4 (November 23, 2023): 169–77. https://doi.org/10.21595/mme.2023.23695.

Copy Chicago

Copied to clipboard!

A mathematical model and microcontroller-based method for measuring dielectric permittivity and discharge characteristics with Arduino ATmega 328: a case study in a physics laboratory

Abstract

Highlights

1. Introduction

2. Research methods

2.1. Materials

2.2. Instrumentations

2.3. Methods

3. Mathematical model

4. Results and discussions

5. Conclusions

References

About this article

Related Articles