Assessment of cracks in beams using changes in the measured frequencies and Particle Swarm Optimization

1. Introduction

Beam-like structures are commonly used nowadays in various domains. Early detection of issues in such structures can save time, money, and even lives. One noninvasive method often used is based on natural frequencies of beams. Numerous studies have been conducted to identify the location and depth of damage [1]-[3]. Recent developments in machine learning have shown promise in Structural Health Monitoring (SHM). This problem has been studied intensively, applying different techniques that involve vibration analysis.

Khatir et al. [4] introduce a technique for detecting and localizing an open crack in beam-like structures using experimentally measured natural frequencies and the Particle Swarm Optimization (PSO) method. The technique considers the variation in local flexibility near the crack. The algorithm minimizes the differences between measured and calculated frequencies.

Ghannadiasl et al. [5] used three hybrid Particle Swarm Optimization algorithms (combined with other algorithms) to predict the location and depth of a crack in a beam by measuring its natural frequency. They concluded that two of the three algorithms produced a strong correlation between the changes in the natural frequency of a concrete beam and the crack parameters. Thus, the measured natural frequency can be used as the input parameter of these algorithms.

Baghmisheh et al. [6] used a rotational spring model of the crack to compute the natural frequencies of cracked beams. They also use the frequency response and modal analysis for measured natural frequencies. Estimating a crack location and depth in a cantilever beam is formulated as an optimization problem, and the optimal location and depth are found by minimizing the cost function based on the difference of the first four measured and calculated natural frequencies.

They applied a hybrid particle swarm–Nelder–Mead (PS–NM) algorithm to estimate the crack location and depth; they first used a modified particle swarm optimization algorithm (PSO), aimed to identify the most promising areas, and a Nelder–Mead simplex algorithm (NM) for performing local search within these areas.

In the paper [7], the authors have successfully enhanced the Grey Wolf Optimizer algorithm for detecting damage in high-dimensional problems. Their research involves the development of a deep convolutional network followed by multivariate linear regressors to detect, assess, and pinpoint damage within a structural beam. Encouraging results have been obtained, particularly when the damage exceeds 10 % of the cross-sectional area of the structure.

In prior research [8], we introduced a novel cost function that leverages the concept of Relative Frequency Shifts (RFS) in the structural assessment for the detection, localization, and evaluation of transverse cracks in simply supported beams. We sought to validate the reliability of this developed method by utilizing RFS values derived from Finite Element Method (FEM) simulations encompassing various damage scenarios. This validation process is illustrated through the presentation of 3D surfaces. In this paper, we define a cost function and show how the PSO algorithm can be used to identify the location and severity of cracks.

2. Particle swarm optimization

PSO is a population-based technique where multiple particles form a swarm, with each particle representing a candidate solution. These particles cooperate as they search for the best solution within a set of possible solutions. Throughout iterations, each particle keeps track of its personal best solution, and the best solution within the swarm. They adjust their flying speed and position based on their experiences and interactions with neighbors. The swarm of particles works together to find the global optimum, ultimately solving the optimization problem. Next, we will define the mathematical model, including parameters and equations, that constitute the PSO algorithm:

where $w$ is an inertia weight parameter, $\left\{x^{Pb,j}\right\}$ is a vector of the own best location found by the particle $j$ until the current iteration, $\left\{x^{Gb}\right\}$ is a vector of the global best location found by the entire swarm up to the current iteration, $v^k\left(t\right)$ is the velocity vector of particle $k$ at time $t$, $\left\{x^j\left(t\right)\right\}$ is the position vector of particle $j$ at time $t$, and $r_1$ and $r_2$ are vectors containing random numbers with uniform distribution in the interval [0, 1].

The fitness of the individual particles reflects the quality of their respective solutions, which is assessed through an objective function. With each iteration, the velocity of particles undergoes a stochastic update.

3. Defining the objective function

In this study, we apply the PSO method to solve the inverse problem of detecting and localizing damage. This result is achieved using a combination of measured and computed natural frequencies. The form of the objective function (OF) is expressed as follows:

where we denoted with $i$ the vibration mode number, with $n$ the total number of modes, with $w_i^c(x,a)$ the computed relative frequency shifts for all considered crack locations $x$ and depths $a$, and with $w_i^m$ the relative frequency shifts obtained from numerical or laboratory experiments. In Eq. (3), $L$ is the beam length, and $d$ is the beam thickness.

To calculate the RFSs, we need to know the frequencies $f_{i-U}$ of the intact beam and those of the beam with a crack, $f_{i-D}$. For the general case, we calculate the RFS values for each vibration mode $i$ with the mathematical relation:

It was shown in [9] that the computed RFSs depend on the crack location and depth by the relation:

In the above equation, ${\left[\stackrel{-}{{\phi }^{\text{'}\text{'}}}\left(x\right)\right]}^2$ is the squared normalized modal curvature, which for the simply supported beam is:

The severity of the damage can be computed using the method presented in [10]; it is based on the mathematical relation:

The deflection increase described in [11].

We created a database containing the computed RFS values for the initial eight transverse vibration modes of a simply supported steel beam measuring $L=$1 m. The beam is subject to transverse cracks of various depths, starting with depth zero and ending with the thickness of the beam. The database is easily generated using Eq. (5).

From the experiments, we find the frequencies of the intact and cracked beam and calculate the measured RFSs using Eq. (4). If we subtract the measured RFSs from these values in the database and obtain eight functions, one for each vibration mode, as illustrated in Fig. 1. The objective function is obtained by superposing the eight functions; it takes the value zero for the crack location and severity.

Fig. 1RFS differences derived for several vibration modes

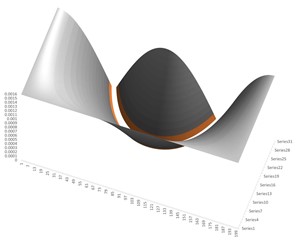
a) First vibration mode

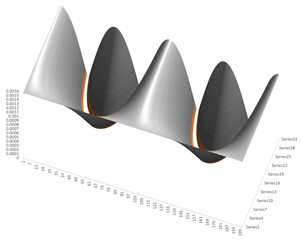
b) Second vibration mode

We boost the accuracy for identifying the crack severity and location when expanding the number of vibration modes. Due to the symmetric nature of the boundary conditions applied to the simply supported beam, the objective function will always reveal two symmetrical potential damage sites.

4. Module interface

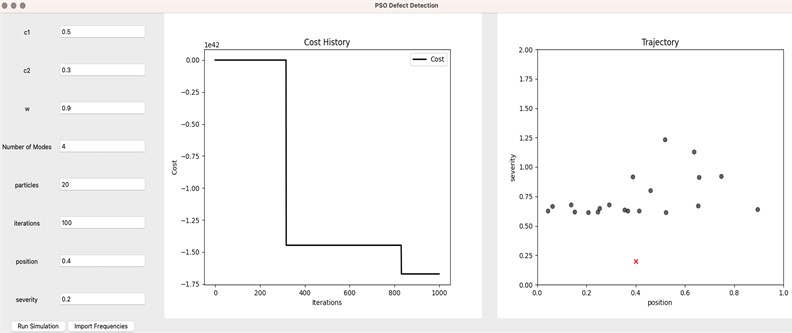
We have implemented our PSO algorithm in Python with a simple user interface, which can facilitate damage location prediction easily. Fig. 2 shows the main window of the PyPSO application. The application requires input the frequencies of the intact and cracked beam for the number of modes used in the assessment. We can import the measured frequencies as CSV files and select the number of vibration modes we intend to use in the assessment process. After running the application, the predicted solution is marked with a red cross in the trajectory graph. The main window of the application displays the cost history as a function of iterations and the trajectories of the particles as they converge to the solution.

Fig. 2PyPSO Application Interface

5. Validation of the PSO assessment method

We conducted a modal analysis using the ANSYS environment to obtain the natural frequencies of the first eight transverse vibration modes for a standard prismatic beam [11]. Both the intact and damaged cases are analyzed. With this data, we create the 3D objective function after the method described in the previous section. To this aim, we use the PyPSO application.

Among the numerous damage scenarios analyzed, we present the case of a crack located at $x/L=$0.336, with the depth increasing successively. For each depth, this crack produces zero-elevation curves in the 3D surfaces. An example of the normalized crack depth $a/d=$0.21 effect is given in Fig. 1; the curve being represented with a white line.

We ran the PSO algorithm for the measured RFSs found for the crack with the abovementioned location and the severity increasing from 0 and extending towards the opposite face with an increment of 0.05. Table 1 presents the generated crack parameters (position and severity) in the first two columns and the PSO estimation in the following two columns. In the last columns, we also indicate the percentual errors.

Table 1 shows that the crack assessment is highly accurate for almost all crack severities except those achieved in the very early stage when the depth is small and the effect on the dynamic and static behavior of the structure is neglectable. A false alarm is launched for the intact beam because the measured RFSs are null, similar to the RFSs for any severity at the hinged beam ends. The location is still identified correctly for the biggest severity, assimilated with the almost sectioned beam, but the severity is supra-estimated.

The most relevant crack parameter, namely the location, is found precisely for almost all crack severities, even for the cracks with small extents. This achievement demonstrates that the PSO, in combination with the RFS-based objective function, can accurately identify cracks in beams if the boundary conditions of the beams are known.

6. Conclusions

We proposed a method for predicting the location and severity of a crack in prismatic beams based on the RFSs and PSO. The algorithm is implemented in Python and permits an easy, fast, and accurate assessment of the crack parameters. From the tests performed, we obtained excellent estimations, both for the crack position and severity. Except for the case without damage, which is wrongly assimilated to damage at the hinged end of the beam, we obtained the most significant error (2 %) for the severity 0.05. For larger cracks, the errors in finding the crack position are less than 0.02 %, meaning 20 mm for a structure of 10 meters long.

Feature research will concern the case of multiple cracks and the identification of cracks in changing environmental conditions. We will also focus on optimizing the PSO parameters for more accurate predictions.