Kinematics design and statics analysis of novel 6-DOF passive vibration isolator with S-shaped legs based on Stewart platform

1. Introduction

In most cases, Vibration is undesirable to machines and structures because it will fatigue, damage, noise, and precise problems [1, 2]. In particular, the vibration has big problems with precise equipment such as highly precise payloads. Therefore, a high-quality vibration isolators are widely used in automotive mechanical engineering, e.g. suspension systems [3] in the protection of equipment requiring high precision [4]. Lower resonant frequencies are often used to achieve better isolation performance, but in such cases, the load capacity of the whole system will be lower or the stiffness will decrease [5]. Therefore, emphasis is placed on active and semi-active vibration control methods to overcome the above drawbacks of traditional passive vibration control [3, 6, 7]. Active isolation uses actuators and sensors that provide force and signals, resulting in large energy consumption and component failure. With the damping characteristics being controlled, vibration isolators using MRF (MRF- Magnetorheological fluid) have attracted the attention of many researchers [8-10]. Excellent dynamic properties such as strong repulsive force, quick response, eco-friendly properties, and low power consumption [5] provide excellent semi-active vibration control ability, which is useful for large machines and high speed machines. Recently, with the theory of nonlinear mechanics, the application potential of isolators has been enhanced to achieve excellent vibration isolation performance [11-21]. These isolation methods can be effective for both low and high frequencies by taking advantage of their nonlinearity. Many mechanisms have historically worked in different areas of vibration isolation, including serial, parallel and hybrid mechanisms. Vibration isolation is the direction of research on devices and methods to reduce harmful vibrations. Classified according to the energy aspect, the basic vibration isolation methods include passive, active and semi-active isolation. Passive isolation is a method of reducing vibrations that do not use additional external energy sources. Energy transfer, if any, will only be in one direction from the system to the outside. Active isolation is a vibration reduction method that uses external energy sources and this energy can be directly fed into the structure through actuators. Semi-active isolation is a vibration reduction method that uses an external energy source but is not directly applied to the main structure, but to passive devices attached to the structure. This means that energy is released from the structure but with regulation from a small external energy source. These are also known as controlled passive devices. The semi-active isolation method has the simplicity and reliability of the passive method, while having the adaptation of the active method.

Remarkably, a biologically derived X-shaped structure consisting of rods, springs, and shaft joints that have been designed, achieving excellent anti-vibration and stability effects. Can be used to achieve excellent high static and low dynamic properties (stiffness properties for passive vibration isolation). The authors systematically investigated the effects of static and dynamic stiffness and structural parameters in X configuration with symmetric and asymmetrical rod lengths. In nature we easily observe X or Z configurations and have been studied in many works [22-26]. X-shaped and Z-shaped are difficult in fabrication and use many revolute joints so that its occurs many disturbed problems in dynamics equations… S-shape, with the design of reasonable parameters (thickness, radius of curvature...), the legs can be subjected to axial compression, the bending part will be very small compared to compression. We almost ignore the problem of nonlinearity in the dynamics equation of the mechanism.

In this study, the S-shaped structure is used as the leg of a novel Stewart platform-based isolator (high nonlinear characteristics, flexibly in space-restricted sites) which has never been studied before. A new passive Stewart platform was designed with an S configuration structure, extensive simulation results were performed, demonstrating excellent tunable stiffness characteristics at low and high resonance frequencies at all 6-DOF. S-shaped is an easy fabricate, the statics and dynamics stiffness problems are better than X-shaped and Z-shaped, so it can be used to remove the high nonlinear dynamics problems of the systems.

There are many vibration isolators centered on one degree of freedom (1-DOF). These isolators use elastic structures to absorb and reduce vibrational energy. This prevents the isolator from operating uniformly in all directions. That makes the isolation effective only in one direction or 1 degree of freedom (1-DOF), for example dampers using springs, it can only reduce vibrations by only 1-DOF along the longitudinal axis of the spring. Vibrations are often multidirectional, so this limits the isolation performance in practical applications. The energies of these vibrations are usually multidirectional with multiple degrees of freedom. In order to achieve better vibration isolation, vibration isolation systems with multiple DOF are being researched [27-31].

In this research, we study a parallel structure passive mechanism based Stewart seismic isolation platform with vertical S-legs, and consider multi-directional nonlinear isolation simultaneously. The parallel structure is a closed dynamic series, all the legs are connected from the origin by parallel links. This link allows for greater accuracy and higher speed. The parallel structure has better performance than the serial structure in terms of accuracy, acceleration speed and high rigidity. They are therefore perfectly suited for industrial applications, such as high-speed micromachining. One of the most popular sets of parallel structures is the 6-degree-of-freedom (6DOF) Stewart Platform which was proposed by Stewart in 1965. It consists of a top plate (moving platform), a base plate (fixed base) and six legs using 12 spherical joints connecting the top plate to the bottom plate. Although this particular S configuration has not been studied before, it has installation advantages and is of practical importance. With the use of the multi-degrees of freedom Stewart platform (6DOF in this study) vibration nonlinear stiffness/damping characteristics, this isolator exhibits excellent anti-vibration performance in six directions, with sufficiently high load carrying capacity, low resonance frequency, and adjustable functional performance through structural parameters and other analysis results are shown. This has the potential to provide an innovative, passive solution for many multi-degree-of-freedom isolation.

This article consists of 3 parts. Firstly, the 6-DOF vibration isolator with the S-shaped leg based on the Stewart platform is proposed, 6-DOF vibration isolator leg is studied with selected structural parameters. Secondly, its kinematics problems and stiffness matrix are considered. Thirdly, analytical studies on the isolation performance of the 6-DOF vibration isolator will be studied with the exciting vibration frequency respectively 5 Hz, 10 Hz, 15 Hz, 20 Hz, and 25 Hz with applied force 30 N. Finally, some conclusions are given.

2. Kinematics and Design of 6-DOF passive vibration isolator with S-Shaped Limbs

2.1. Introductions to 6-DOF passive vibration isolator base on Gough-Stewart platform

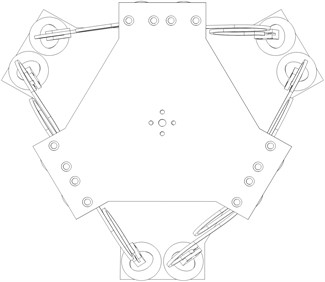
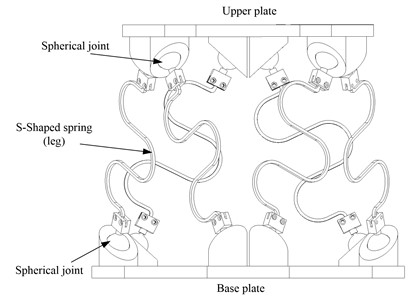
Based on the advantages of the Stewart platform, the passive isolators design features the shape of the Stewart platform type 6-6. Dimensions of isolators (diameter of moving plate and fixed plate, length of legs) were determined based on the optimal position of the mechanism, with design adjustments added. The 6 DOF Passive Isolator – based Stewart Platform is a compliance using parallel mechanism in which the movable base is connected to the fixed base by S-shaped pins via spherical joints. In this design, as shown in Fig. 1, the Stewart-type 6DOF passive isolation platform has 6 S-shaped chains link the fixed base and the movable platform through 12 spherical joints.

Fig. 1Geometric plan view of 6-DOF passive vibration isolator type Gough-Stewart platform

2.2. Kinematics of 6-DOF passive vibration isolator

The screw theory is an elegant and powerful method to investigate the kinematics and statics of serial and parallel manipulators. In [32], authors defined a screw as a straight line with which a definite linear magnitude termed the pitch. The pitch is the rectilinear distance through which the nut is translated parallel to the axis of the screw, while the nut is rotated through the angular unit of circular measure. A screw is essentially a geometrical concept. Any system of forces and couples acting on a rigid body can be represented by a wrench with a certain intensity on a screw. Similarly, any velocity or infinitesimal displacement of a rigid body can be expressed by a twist of a certain magnitude about a screw.

The parallel mechanism of passive isolators simultaneously reduces force and displacement by converting a small infinitesimal between two rigid bodies into corresponding wrenches acting between them. The simple, real-time response of passive isolators eliminates the complex controls and sophisticated instrumentation required in some applications such as highly precise payload in UAVs or in autonomous equipment.

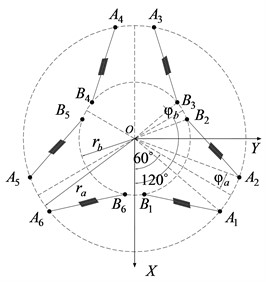
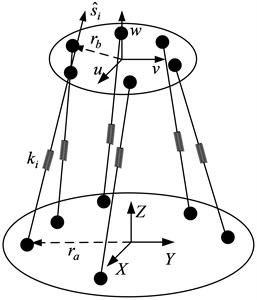
In Fig. 1, $r_a$ and $r_b$ are radius of base and top plate. The linkage joints are spherical joints at $A_i$, $B_{i}i=$ 1, ..., 6. Also, ${\phi }_a$ and ${\phi }_b$ are the half angles of the adjacent spherical joints. Since the configuration with the isotropic eigen values should be symmetric with respect to geometry, the statically optimal configurations will be investigated in a symmetric configuration. The distance between base and top plate is $p$ along the $Z$ axis. The locations of the spherical joints with respect to the base frame $\left\{B\right\}$ can be expressed by:

1

$\begin{array}{c}{\mathbf{a}}_i=r_a[\mathrm{c}\mathrm{o}\mathrm{s}{\mathrm{\Lambda }}_i,\mathrm{s}\mathrm{i}\mathrm{n}{\mathrm{\Lambda }}_i,0{]}^T,{\mathbf{b}}_i=r_b[\mathrm{c}\mathrm{o}\mathrm{s}{\lambda }_i,\mathrm{s}\mathrm{i}\mathrm{n}{\lambda }_i,0{]}^T,i=1,2...,6,\end{array}$

where ${\mathrm{\Lambda }}_i=\frac{\pi }{3}i-{\phi }_a$for $i=1,3,5$; ${\mathrm{\Lambda }}_i=\frac{\pi }{3}(i-1)+{\phi }_a$ for $i=2,4,6$ and ${\lambda }_i=\frac{\pi }{3}(i-1)+{\phi }_b$ for $i=1,3,5$; ${\lambda }_i=\frac{\pi }{3}i-{\phi }_b$ for $i=2,4,6$.

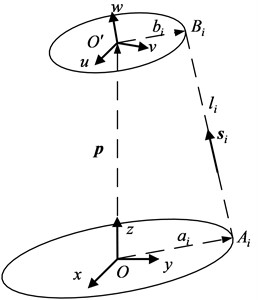
Fig. 2Vector loop of a Gough-Stewart platform

Since all rotation take place about the coordinate axes of a fixed frame the resulting rotation matrix is obtained by pre-multiplying three basic rotation matrices:

2

$\begin{array}{l}{}_{}{}^A{R}_B=Rot(z,\gamma )\cdot Rot(y,\beta )\cdot Rot(x,\alpha )=\left[\begin{array}{ccc}c\alpha & -s\alpha & 0\\ s\alpha & c\alpha & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}c\beta & 0& s\beta \\ 0& 1& 0\\ -s\beta & 0& c\beta \end{array}\right]\left[\begin{array}{lll}1& 0& 0\\ 0& c\gamma & -s\gamma \\ 0& s\gamma & c\gamma \end{array}\right]\\ =\left[\begin{array}{lll}c\beta c\alpha & s\gamma s\beta c\alpha -c\gamma s\alpha & c\gamma s\beta c\alpha +s\gamma s\alpha \\ c\beta s\alpha & s\gamma s\beta s\alpha +c\gamma c\alpha & c\gamma s\beta s\alpha -s\gamma c\alpha \\ -s\beta & s\gamma c\beta & c\gamma c\beta \end{array}\right],\end{array}$

where $s\alpha =\mathrm{s}\mathrm{i}\mathrm{n}\alpha$, $c\alpha =\mathrm{c}\mathrm{o}\mathrm{s}\alpha$, $s\beta =\mathrm{s}\mathrm{i}\mathrm{n}\beta$, $c\beta =\mathrm{c}\mathrm{o}\mathrm{s}\beta$, $s\gamma =\mathrm{s}\mathrm{i}\mathrm{n}\gamma$, $c\gamma =\mathrm{c}\mathrm{o}\mathrm{s}\gamma$.

As shown in Fig. 2 let ${\mathbf{a}}_i=[a_{ix},a_{iy},a_{iz}{]}^T$ and ${}_{}{}^B\mathrm{}{\mathbf{b}}_i=[b_{iu},a_{iv},a_{iw}{]}^T$ be the position of point $A_i$ and $B_i$ in the coordinate frame $\left\{A\right\}$ and $\left\{B\right\}$, respectively. We can write a vector loop equation for the $i$th limb of the manipulator as follows:

3

$\overline{A_i{B}_i}=\mathbf{p}+{}_{\mathrm{}}{}^A\mathrm{}{R}_B{}_{\mathrm{}}{}^B\mathrm{}{\mathbf{b}}_i-{\mathbf{a}}_i.$

The length of the $i$th limb is obtained by taking the dot product of the vector $\overline{A_i{B}_i}$ with itself. Rewrite in vector form the limb lengths can be obtained as:

4

${\mathbf{l}}_i={}_{\mathrm{}}{}^A\mathrm{}{R}_B{}_{\mathrm{}}{}^B\mathrm{}{\mathbf{b}}_i+\mathbf{p}-{\mathbf{a}}_i,$

or:

5

$l_i=‖{\mathbf{l}}_i‖=‖{}_{\mathrm{}}{}^A\mathrm{}{R}_B{}_{\mathrm{}}{}^B\mathrm{}{\mathbf{b}}_i+\mathbf{p}-{\mathbf{a}}_i‖,\mathrm{}\mathrm{}\mathrm{}\mathrm{}i=1,2...,6.$

Equation above written six times, yield six equations describing the location of the moving platform with respect to the fixed base.

2.3. Design of a 6-axis passive vibration isolator

As shown in Fig. 1, the Screw direction vector can be expressed by:

6

$\begin{array}{l}{s}_{1x}=\frac{-r_a\mathrm{c}\mathrm{o}\mathrm{s}(2\pi /3+{\phi }_a)-r_b\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_b}{L}=0,\\ s_{1y}=\frac{-r_a\mathrm{s}\mathrm{i}\mathrm{n}(2\pi /3+{\phi }_a)+r_b\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_b}{L}=-\frac{1}{\sqrt{2}},\\ s_{1z}=\frac{h}{L}=\frac{1}{\sqrt{2}}.\end{array}$

Rewritten the equation Eq. (6) as:

7

$\begin{array}{l}{r}_a\mathrm{c}\mathrm{o}\mathrm{s}(2\pi /3+{\phi }_a)+r_b\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_b=0,\\ -r_a\mathrm{s}\mathrm{i}\mathrm{n}(2\pi /3+{\phi }_a)+r_b\mathrm{s}\mathrm{i}\mathrm{n}{\phi }_b=-\frac{L}{\sqrt{2}}\\ h=\frac{L}{\sqrt{2}}.\end{array},$

Solving equation Eq. (7) yields:

8

$\begin{array}{l}{r}_a=\frac{\frac{L}{\sqrt{2}}}{\left[\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{2\pi }{3}+{\phi }_a\right)+\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{2\pi }{3}+{\phi }_a\right)\mathrm{t}\mathrm{a}\mathrm{n}{\phi }_b\right]},\\ r_b=-\frac{r_a\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{2\pi }{3}+{\phi }_a\right)}{\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_b},\\ h=\frac{L}{\sqrt{2}},\end{array}$

where, when $L=L_0$ then $h=h{}_0{}^{\mathrm{}}$. The parameters and 3D model of 6-DOF passive vibration isolator type Gough-Stewart platform structure with S-shape limb expressed in Table 1 and Fig. 3.

Table 1Parameters of compliance

Dimension of moving base $r_b$	106 mm
Dimension of fixed base $r_a$	134 mm
Length of leg (initial) $L_0$	180 mm
Height (initial) $h_0$	214 mm
Thickness of leg	2 mm
Radius of curvature (of leg)	17.5 mm
Half angles of the adjacent spherical joints ${\phi }_a$	6.9°
Half angles of the adjacent spherical joints ${\phi }_b$	11.3°

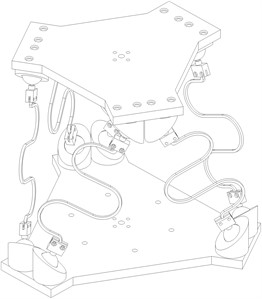
As shown in Fig. 3, we designed an S-Shaped legs for the compliance that can isolate vibrations. With the design of reasonable parameters (thickness of 2 mm, radius of curvature of 17,5 mm...), the legs can be subjected to axial compression, the bending part will be very small compared to compression. A 3D structural drawing of the S-shaped Stewart platform is shown in Fig. 3. This platform can protect the isolated object from various excitations (horizontal, vertical and rotational) on the base.

Fig. 3Prototype of 3D model of 6-DOF passive vibration isolator with S-Shaped leg

2.4. Stiffness mapping of the spatial 6-axis compliance device

The analysis of stiffness matrix for the spatial stiffness (see Fig. 4) property will be explored. An external force ${\mathbf{w}}_0=[{\mathbf{f}}^T,{\mathbf{n}}_0^T{]}^T$ is applied to the moving platform of the parallel manipulator with six connectors. If the moving platform is in equilibrium, the wrench is defined as:

9

$\mathbf{w}={\tau }_1{\widehat{\mathbf{s}}}_1+{\tau }_2{\widehat{\mathbf{s}}}_2+\cdots +{\tau }_6{\widehat{\mathbf{s}}}_6=J\mathbf{\tau },$

where $J=[{\widehat{\mathbf{s}}}_1,{\widehat{\mathbf{s}}}_2,{\widehat{\mathbf{s}}}_3,{\widehat{\mathbf{s}}}_4,{\widehat{\mathbf{s}}}_5,{\widehat{\mathbf{s}}}_6]$ and $\mathbf{\tau }=[{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,{\tau }_5,{\tau }_6{]}^T$.

Jacobian matrix mapping the input forces to the output wrench is given by:

10

$J=\left[\begin{array}{ccc}\mathbf{s}{}_1{}^{\mathrm{}}& ...& \mathbf{s}{}_m{}^{\mathrm{}}\\ \mathbf{r}{}_1{}^{\mathrm{}}\times \mathbf{s}{}_1{}^{\mathrm{}}& ...& \mathbf{r}{}_m{}^{\mathrm{}}\times \mathbf{s}{}_m{}^{\mathrm{}}\end{array}\right],$

and ${\tau }_i=k_i(l_i-l_{0i})$, $k_i$ is the stiffness constant of limb $i$th.

The infinitesimal change of the wrench can be written as:

11

$\delta \mathbf{w}=J\left[k\right]\delta \mathbf{l}.$

The relationship between an infinitesimal change the length of limb and the infinitesimal change in twist can be expressed as:

12

$\delta \mathbf{l}=J^T\delta \mathbf{D}.$

When the external force has an infinitesimal change $\mathbf{\delta }\mathbf{w}$, the upper platform has an infinitesimal displacement along an axis. The stiffness matrix $K$ is a transformation matrix that changes the infinitesimal change in applied wrench $\mathbf{\delta }\mathbf{w}$ to the infinitesimal change in twist $\mathbf{\delta }\mathbf{D}$ (stiffness mapping) obtain as:

13

$\delta \mathbf{l}=J^T\delta \mathbf{D},$

where $\delta \mathbf{D}=[\delta {\mathbf{p}}^T,\delta {\mathbf{\theta }}^T]$ and $K$ is the stiffness matrix.

The stiffness matrix $K$ is written in method from as [33]:

14

$K=J\left[k_i\right]J^T,\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}i=1,\dots ,6,$

where $\left[k\right]$ is a diagonal matrix whose diagonal entries are the spring stiffness and ${\rho }_i=l_{oi}/l_i$ and $J$ is Jacobian matrix.

Jacobian matrix can be written as:

15

$J=\left[{\widehat{\mathbf{s}}}_1,{\widehat{\mathbf{s}}}_2,{\widehat{\mathbf{s}}}_3,{\widehat{\mathbf{s}}}_4,{\widehat{\mathbf{s}}}_5,{\widehat{\mathbf{s}}}_6\right],$

where ${\mathbf{s}}_i$ is screw direction vector of limb $i$th.

Fig. 4Compliance coupling

Fig. 5Gough-Stewart of type 6-6 passive isolation platform geometry

In order to use the 6-asix passive vibration isolator type Stewart platform, the forward kinematics computation to obtain for measured spring lengths has to be performed and thereby the stiffness matrix expressed by equation 14 can be determined. Based on the stiffness matrix the stiffness of the leg can be chosen for each suitable isolation requirement.

2.5. Static stiffness analysis of the novel 6-DOF passive vibration isolator with S-Shaped legs

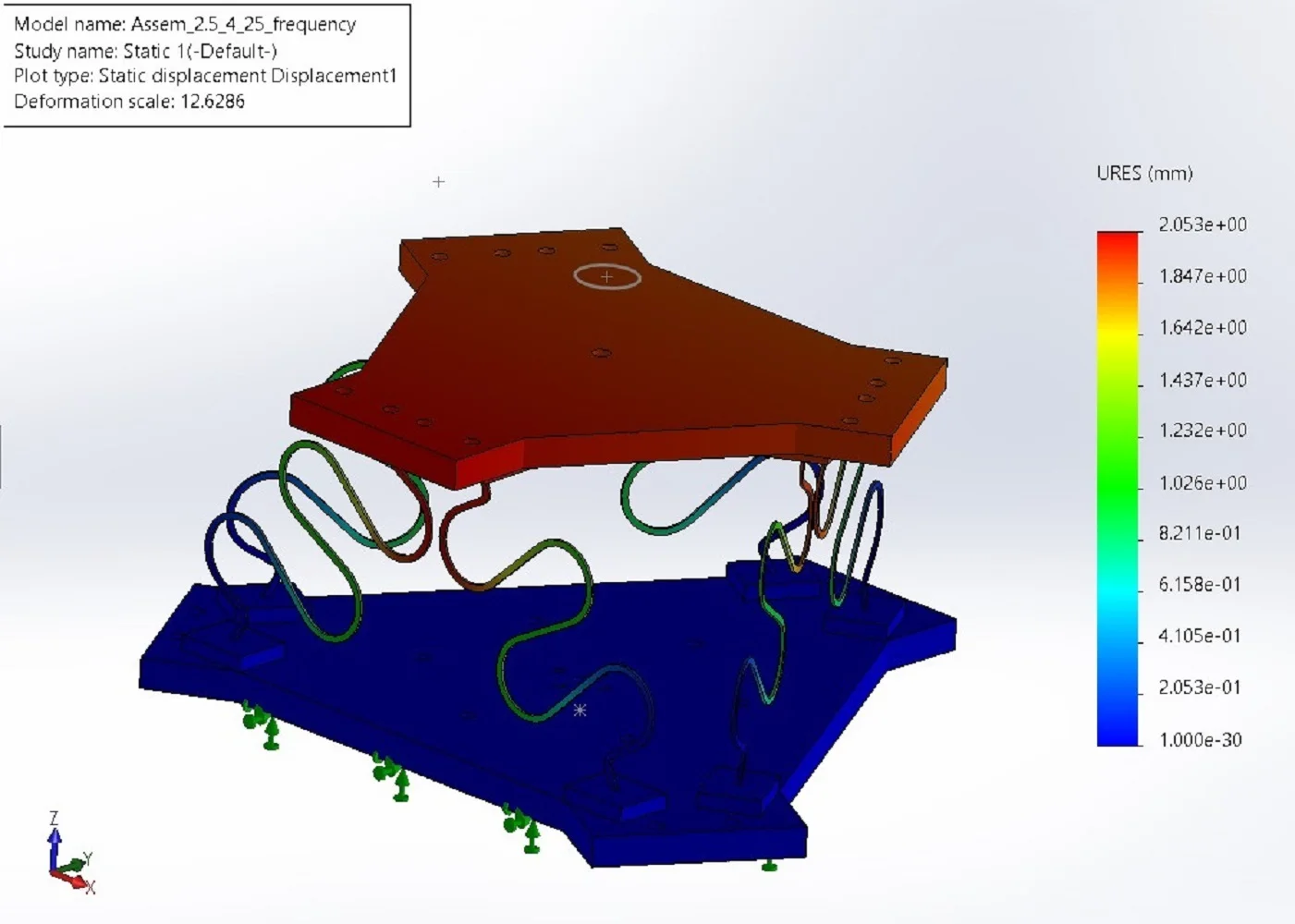
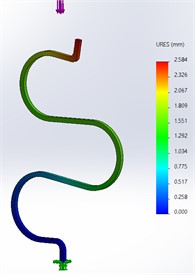
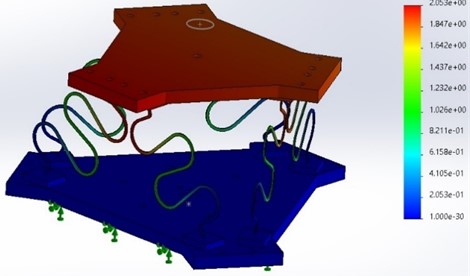
As shown in Fig. 6 is the deformation of model static includes a 1-leg simulation under compression and a 6-degrees-of-freedom mechanism under compression. Upper platform payload is 1,5 kg in vertical direction. The bottom platform is fixed. It can be seen that, when a load-bearing leg has horizontal displacement, however, the mechanism has absolutely no horizontal displacement, only vertical displacement exists. This can be confirmed, by combining the legs together, we have eliminated the horizontal displacement of the legs; the mechanism completely works in the vertical direction.

Fig. 6Evaluation of static simulation model for S-shaped leg and vibration isolator

As shown in Figs. 7 to 11 is the platform response in the time to the vertical excitation and the vibrational signal of the fundamental excitation. The payload on top of the platform is 1,5 kg. The vibration frequency on the bottom platform is respectively 5 Hz, 10 Hz, 15 Hz, 20 Hz, 25 Hz with applied force 30 N. From the graphs above, it can be seen that the vibration at the upper plate has almost exactly described the vibration of the lower plate and has no phase delay. That allows us to conclude that our proposed compliance 6-DOF with leg linkage can be used to isolate vibrations in the vertical direction.

Fig. 7Illustration of the acceleration of fixed plate (blue) and moving plate (red) at 5 Hz

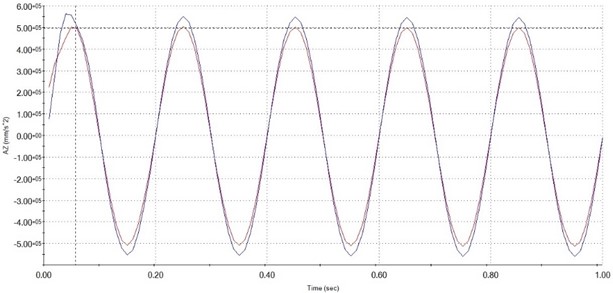
Fig. 8Illustration of the acceleration of fixed plate (blue) and moving plate (red) at 10 Hz

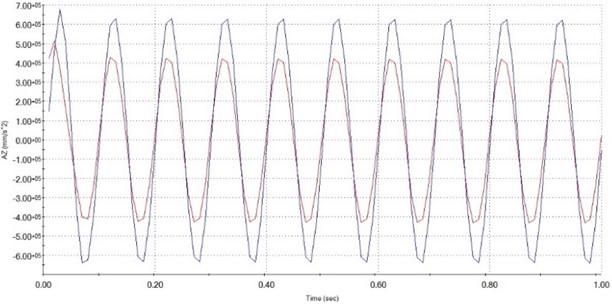
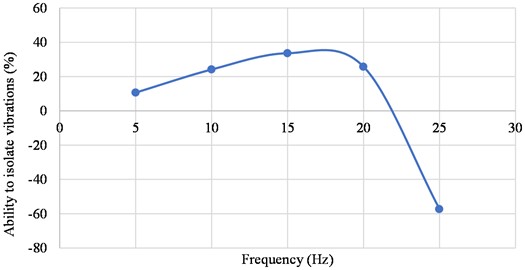
As expressed in Fig. 7 the ability to isolation at different frequencies 10.64 % (5 Hz), 24.15 % (10 Hz), 33.63 % (15 Hz), 25.75% (20 Hz), –57.31 % (25 Hz). From the graph of Fig. 12 we can make a comment, compliance device 6DOF using leg S-shaped configuration effectively isolates in the frequency range below 22 Hz, after this frequency range accelerates obtained at the top plate is larger than the excitation acceleration at the bottom plate, resulting in negative isolation efficiency.

Fig. 9Illustration of the acceleration of fixed plate (blue) and moving plate (red) at 15 Hz

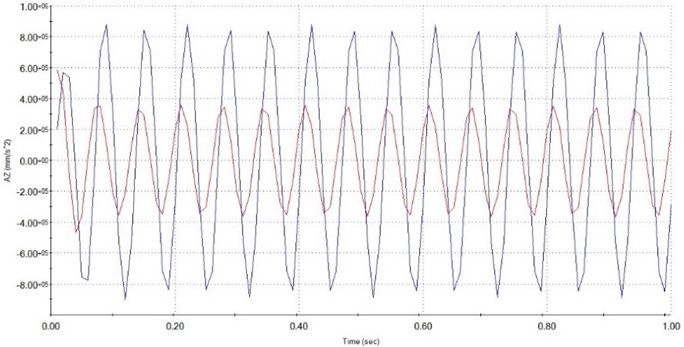
Fig. 10Illustration of the acceleration of fixed plate (blue) and moving plate (red) at 20 Hz

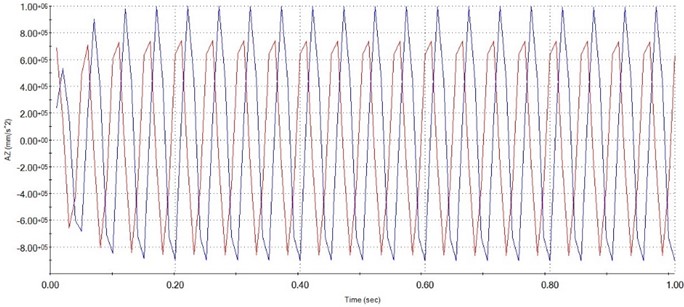
Fig. 11Illustration of the acceleration of fixed plate (blue) and moving plate (red) at 25Hz

Fig. 12Graph shows the ability to isolate vibrations at different frequencies

3. Conclusions

Compliance device is a passive strain sensor, so it helps to avoid collisions in high-precision devices. In addition, it is also a device that is applied for the purpose of protecting machinery from external impacts (shocks), effectively reducing shock, anti-vibration and impact resistance. In this study, the model parameters of compliance device with legs using S-shaped were determined from the results of calculation and simulation. Based on geometrical parameters and vibration sources and some loads assuming the structure's durability problem is solved and evaluated the efficiency of the isolator at different frequencies. This is an important result for further research problems (for example, optimizing the structure, manufacturing and testing isolators and putting them into practical applications....).