Simulation study of crack parameters’ effects on the vibration characteristics of a bladed disk system

Pan, Chuang; Dai, Yuande; Li, Yaocheng

doi:10.21595/jve.2023.23337

Journal of Vibroengineering

Browse Journal

Submit article

Published: 01 August 2023

Check for updates

Simulation study of crack parameters’ effects on the vibration characteristics of a bladed disk system

Chuang Pan¹

Yuande Dai²

Yaocheng Li³

^{1, 2}School of Advanced Manufacturing, Nanchang University, Nanchang, China

³Jiangxi TECO AIR Conditioning Equipment Co., Ltd., Nanchang, China

Corresponding Author:

Yuande Dai

Cite the article Download PDF

Downloads 113

Abstract

As a key component of the turbo machine rotor in harsh operating conditions, high cycle fatigue failure and even cracks are common in bladed disks. In this paper, modal analysis was carried out for a single cracked bladed disk system, the effects of crack depth, crack height and rotating speed on its vibration characteristics were studied by the method of both numerical simulation and orthogonal test, and the effects of crack distribution on the vibration characteristics of multi-crack bladed disk systems were also studied. Finally, some conclusions have been drawn, they provide a fundamental understanding of blade health monitoring and fault prediction, and are important to improve the reliability and safety of turbine operation.

Simulation study of crack parameters’ effects on the vibration characteristics of a bladed disk system

Highlights

This paper conducts modal analysis on single crack bladed disk systems and multi crack bladed disk systems by the method of numerical simulation. Studies and summarizes the effects of crack depth, crack distribution, and rotational speed on their vibration characteristics.
This paper found that the number of cracked blades corresponds to the order of the affected natural frequency. When the cracked blades are all adjacent to each other, the first-order natural frequency of the bladed disk is the smallest and the maximum first-order amplitude is the largest.
This article studies the effects of crack depth, crack height, and blade speed on the natural frequency of a single crack blade disk system through a combination of orthogonal experiments, range analysis, and variance analysis. It was found that they had no significant impact on the natural frequencies of the blade disk system.

1. Introduction

The bladed disk is an important energy conversion component in the turbine, and due to its harsh working environment, it is often subjected to alternating mechanical and thermal stresses and is therefore prone to fatigue failure [1], [2]. Fatigue failure is generally manifested as the blade fatigue cracks [3]-[4]; crack generation and expansion will lead to a change in the vibration characteristics of the bladed disk, which will lead to a serious blade fracture [5]-[7]. With the development of turbine and gas turbine technology, due to its increasing capacity and speed, the requirements for its core component blade structure performance also increased [8]-[10]. Therefore, it is necessary to study the vibration characteristics of the bladed disk system with cracks.

In recent years, many scholars have conducted in-depth studies on the vibration characteristics of bladed disks with cracks. Petyt [11] studied the change of natural frequency with crack depth through experiments and finite element method, which laid the foundation for the research on the aspect of vibration problems of plates with cracks. Ma et al. [12] studied the vibration of cantilever square plates with cracks at the edges using amplitude fluctuation electronic speckle pattern interferometry (AFESPI) set out of the plane and pointed out that the natural frequencies and relevant vibration modes of square plates will also change with the change of crack depth. Huang et al. [13] used numerical simulation to study the effect of crack depth and location on the vibration characteristics of a cantilevered bladed disk structure with a crown ring. Chen et al. [14] investigated the vibration and stability of thick rotating blades with single-edge cracks using finite element models. Hou et al. [15] developed a blade root model with penetrating cracks using the theory of concentration mass beam and used the flexibility matrix method to analyze the dynamic characteristics of bladed disks with different depth of crack detuning systems and found that the presence of cracked blades leads to a significant increase in the response amplitude of other uncracked blades. Hadjileontiadis et al. [16] investigated the dynamic characteristics of a cantilever beam with cracks under simple harmonic excitation and showed that the natural frequency oscillates between the frequencies corresponding to the open and closed states, revealing the crack breathing problem and demonstrating that the depth of cracks can be judged by the degree of harmonic distortion. Fang et al. [17] derived the intrinsic relationship between the vibration characteristics of a detuned bladed disk structure containing a single-crack blade and the system parameters such as internal coupling, crack severity, excitation mode, and number of blades by studying the cantilever beam equivalent blade. Saito et al. [18] carried out linear and nonlinear research on frequency steering and mode transformation of a cantilever flat blade, quantitatively analyzed the gradual change process of vibration mode in the frequency steering area, and analyzed the influence of detuning effect, rotation effect, etc. on a single-crack blade and an integral blade disk by using the modal synthesis method. Liu et al. [19] used the hexahedral finite element method to analyze the dynamics of the cracked blade, compared the breathing effect of the cracked blade and the natural frequency at different crack depths with the calculation results of the contact unit method, and found that the calculation results of the hexahedral unit are in good agreement with the contact finite element calculation results. The above research results show that the crack depth and crack location are two important factors affecting the vibration characteristics of the bladed disk [20], [21]; however, there is a lack of comparative study on the influence of these two factors on the vibration characteristics of bladed disks, as well as the vibration characteristics of bladed disks with multiple cracks.

In this paper, based on the finite element theory, the model of the bladed disk with single crack is established for different crack depths and crack heights, and based on the orthogonal test method, the influence law of different cracks on the vibration characteristics of the bladed disk system under static and dynamic conditions is revealed. Based on the results of the single-crack bladed disk, the influence of crack distribution on the static and dynamic vibration characteristics of the bladed disk system is studied for the double cracked and triple cracked bladed disks, respectively.

2. Modeling

The bladed disk system consists mainly of a wheel disk and blades, and the blades are uniformly distributed on the circumference of the disk. In order to facilitate the study, the bladed disk system is appropriately simplified. Design The diameter of the rotor shaft hole is 200 mm, the diameter of the rotor is 400 mm, and the thickness is 24 mm. 12 identical blades are uniformly distributed on the rotor, with a thickness of 8 mm, a length of 120 mm, and a width of 25 mm. The parameters are set: Poisson’s ratio is 0.3, the modulus of elasticity is 200 GPa, the density is 7,800 kg/m³, and the material is 45-gauge steel by default. Generally, there are three types of cracks: penetration cracks, surface cracks, and deeply buried cracks, and the probability of penetration cracks is the highest due to their working environment [22]. Therefore, this paper focuses on the study of penetrating cracked bladed disks, and the system model and mesh division of a bladed disk with a single crack are shown in Fig. 1. The crack depth is denoted by $D$ , and the crack height is the distance from the crack to the root of the blade, denoted by $H$ .

Fig. 1Single-crack bladed disk system model and mesh division

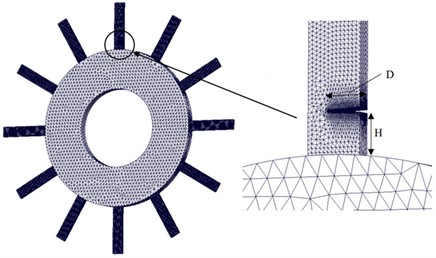
In order to ensure the computational accuracy and save computational resources, four sets of meshes with different sparsities were selected in this paper to simulate the static and dynamic vibration characteristics of the resonant bladed disk, and the results and errors of the first-order natural frequency calculation are listed in Table 1 [23]. It is determined that the number of meshes meets the requirement of computational accuracy at about 274135.

Table 1Basic size and style requirements

Number of grids	First-order static natural frequency / Hz	Error	First-order dynamic natural frequency / Hz	Error
62634	422.45	0.270 %	432.59	0.259 %
151864	421.31	0.1234 %	431.47	0.118 %
274135	420.79	0.088 %	430.96	0.074 %
554926	420.42	–	430.64	–

3. Effect on the vibration characteristics of a single-crack bladed disk system

3.1. Effect of single-crack depth

Constraints are applied to the inner ring of the bladed disk structure, and the crack depth ( $D$ ) of the cracked bladed disk is designed to be 5 mm, 10 mm, and 15 mm, and the first 12th order vibration patterns and natural frequencies are calculated for the harmonic bladed disk system and the cracked bladed disk system, respectively, where the crack height is ( $H$ ) 20 mm and the dynamic bladed disk speed ( $N$ ) is 3000 r/min. the static and dynamic natural frequencies are shown Fig. 2.

Fig. 2Comparison of natural frequency data between tuned bladed disk and cracked bladed disk

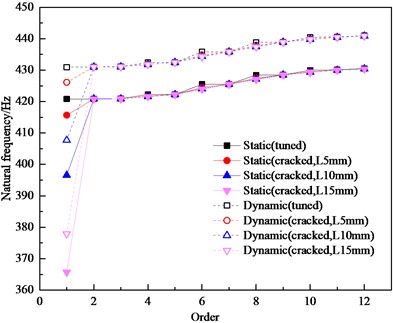
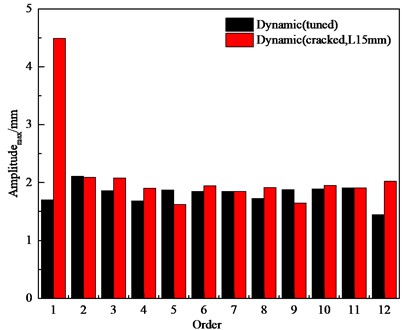
From Fig. 2, it can be seen that the dynamic natural frequency of the bladed disk system is significantly larger than the static natural frequency, mainly because the centrifugal force increases the stiffness of the detuned structure and thus affects its natural frequency, and the static and dynamic natural frequencies of the harmonic bladed disk system basically change linearly with the increase of order [24], [25]. The natural frequencies of the first 12 orders of the harmonic bladed disk and the cracked bladed disk are close but not crossed between the modes of multiple orders, and the natural frequency steering phenomenon does not occur. Whether dynamic or static, the 1st order frequency of the bladed disk structure is significantly reduced by the crack and is positively correlated with the crack depth, while the frequency above the 2nd order does not change much. As a whole, the crack has a relatively large effect on the natural frequency of the structure. The natural frequency of the structure is significantly reduced due to the appearance of cracks, but the difference between the natural frequencies under different operating conditions caused by the appearance of cracks becomes smaller and smaller as the order increases. According to the above analysis, it is found that the natural frequency reduction of the bladed disk system with a crack depth of 15 mm is the most obvious. Therefore, the modal analysis of the bladed disk system with a crack depth of 15 mm is carried out, and the dynamic mode vibration pattern of the first 12 orders is shown in Fig. 3. The trend of the amplitude_max (maximum amplitude) of the harmonic bladed disk and the cracked bladed disk ( $D =$ 15 mm) with the modal variation is shown in Fig. 4. The amplitude of each blade is evenly distributed under different modes of the harmonic bladed disk, while the amplitude_max of the cracked bladed disk appears on the cracked blade in the first-order mode, and the amplitude is significantly higher than that of other blades.

Fig. 3First twelve-order mode shapes of tuned bladed disk and cracked bladed disk

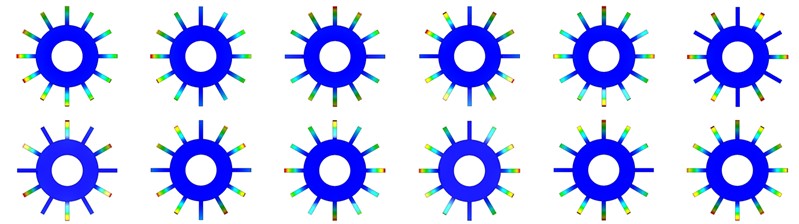
a) First twelve-order modes of tuned bladed disk

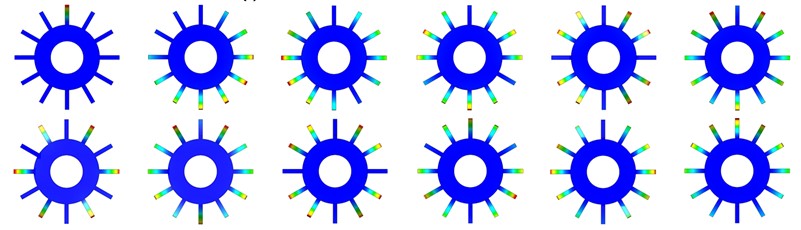
b) First twelve-order modes of cracked bladed disk

Fig. 4First twelve-order amplitudemax of tuned bladed disk and cracked bladed disk system

3.2. Effect of single-crack height

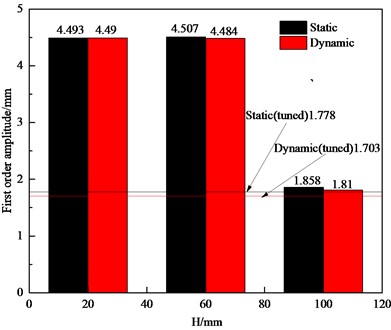
The location of the crack generation is random, and the location of the crack affects the vibration characteristics of the bladed disk to different degrees [26], [27]. The location of the crack in a single-crack bladed disk system shows the crack height. In order to get more obvious results, cracks with a crack depth of 15 mm and crack heights of 20 mm, 60 mm, and 100 mm were established on a single blade. and the natural frequencies of the bladed disk structure under both static and dynamic (3000 r/min) operating conditions were further analyzed, and after modal analysis, the first 12 orders of magnitude of static and dynamic for the cracked bladed disk system with different crack locations were obtained. The natural frequencies are shown in Fig. 5. The dynamic natural frequency is still always higher than the static natural frequency, and as the crack height increases, the influence of the crack on the natural frequency of the bladed disk gradually decreases. When the crack height is 100 mm, the effect of the crack on each order of natural frequency is almost 0. The trend of the first-order amplitude_max with the crack height is shown in Fig. 6, and the dynamic and static first-order amplitudes_max of the cracked bladed disk are basically equal. When the crack height is 20 or 60 mm, the first-order amplitude_max of a cracked bladed disk in dynamic and static conditions is about 2.5 times that of the harmonic bladed disk. When the crack height is 100 mm, the first-order static amplitude_max of the cracked bladed disk is about 4.5 % higher, and the dynamic first-order amplitude_max is about 1.8 % higher compared with the harmonic bladed disk. The effect of a crack height below 60 mm on the amplitude_max of the bladed disk is obvious, and the effect on the amplitude_max of the bladed disk decreases gradually with the increase of the crack height between 60 and 100 mm. The effect of a crack height around 100 mm on the amplitude_max of the bladed disk is negligible.

Fig. 5Different order natural frequencies of bladed disks with different crack heights

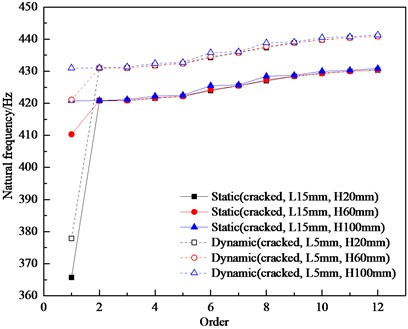
Fig. 6First order amplitudesmax of bladed disks with different crack heights

4. Dynamic vibration characteristics of a single-crack bladed disk

The above results show that the crack depth and crack height are important factors affecting the detuning of the bladed disk. In addition, the rotational speed of the bladed disk also has a certain influence on the vibration characteristics of the bladed disk. In order to comprehensively consider the degree of influence of crack depth, location, and rotational speed of the bladed disk on the first-order natural frequency and amplitude_max of the bladed disk, a three-factor, three-level orthogonal test table was used to investigate the first-order natural frequency and first-order amplitude_max of the cracked bladed disk under dynamic conditions. The crack depths are 5 mm, 10 mm, and 15 mm; the crack heights are 20 mm, 60 mm, and 100 mm; and the rotational speed of the bladed disk is 2000 r/min, 3000 r/min, and 4000 r/min. The dynamic vibration characteristics obtained by the orthogonal test design scheme are shown in Table 2.

Table 2Dynamic vibration characteristics orthogonal test table

Number	$D$ / mm	$H$ / mm	$N$ / r/min	Error	First-order natural frequency / Hz	First-order amplitude_max / mm
1	5	20	2000	1	420.4	4.17
2	5	60	4000	2	436.00	3.91
3	5	100	3000	3	431.0	2.07
4	10	20	4000	3	416.1	4.46
5	10	60	3000	1	428.1	3.96
6	10	100	2000	2	425.4	2.22
7	15	20	3000	2	377.9	4.49
8	15	60	2000	3	415.7	4.50
9	15	100	4000	1	438.7	1.79

4.1. Range analysis

With the advantages of simple calculation and intuitive results, the range analysis method is widely used in data analysis. The degree of influence of crack depth, crack height, and bladed disk rotational speed on the first-order natural frequency and amplitude_max are studied separately by the range analysis method to obtain the primary and secondary orders of these three parameters, and according to the test results of each row of factor level numbers, the combination that has the greatest impact on the vibration characteristics of the blade disk is obtained.

Table 3Results of the range analysis

Parameter	First-order natural frequency				First-order amplitude_max
Parameter	$H$	$D$	$N$	Error	$H$	$D$	$N$	Error
$K_{1}$	1287.34	1214.37	1260.86	1287.20	10.16	13.13	10.89	9.92
$K_{2}$	1269.59	1279.30	1237.02	1239.27	10.64	12.37	10.52	10.62
$K_{3}$	1231.79	1295.05	1290.84	1262.25	10.78	6.08	10.17	11.03
$K_{1}$	429.11	404.79	420.29	429.07	3.39	4.38	3.63	3.31
$K_{2}$	423.20	426.43	412.34	413.09	3.55	4.12	3.51	3.54
K₃	410.60	431.68	430.28	420.75	3.59	2.03	3.39	3.68
Range	18.52	26.89	17.94	15.98	0.21	2.35	0.24	0.37
Primary relation	$H > d > n > e$				$H > e > n > d$
Optimal combination	D₃H₁N₂				D₃H₁N₁

The results of the extreme difference analysis are shown in Table 3. The range corresponding to the first-order natural frequency $R_{H} > R_{D} > R_{N} > R_{E}$ , so the major and minor order of the degree of influence of the first-order natural frequency is: crack height, crack depth, and bladed disk speed. The lower the first order natural frequency is, the greater the influence of factors on the bladed disk is. Therefore, D₃H₁N₂ has the greatest influence on the first order natural frequency. The modal analysis of the cracked bladed disk with the combination D₃H₁N₂ shows that the first-order natural frequency is 377.91 Hz, which is smaller than the results of other combinations in the orthogonal test table, verifying the accuracy of the range analysis. The first-order amplitude_max corresponds to the range $R_{H} > R_{E} > R_{N} > R_{D}$ , so the influence of the first-order amplitude_max is in the following order: crack height, bladed disk speed, and crack depth. The larger the first-order amplitude_max, the greater the degree of influence, so the combination with the greatest influence on the first-order amplitude_max is D₃H₁N₁. The modal analysis of the cracked bladed disk with the combination D₃H₁N₁ shows that its first-order amplitude_max is 4.51 mm, which is larger than the results of other combinations in Table 3, which also verifies the accuracy of the range analysis.

4.2. Analysis of variance

The range analysis method can only determine the order of the factors and the optimal combination of parameters, but cannot determine the magnitude of the error and the degree of influence of the test results of each factor, so it is necessary to test the magnitude of the error by other analysis methods [28]. Therefore, it is necessary to check the magnitude of the error by other analysis methods. The ANOVA (analysis of variance) was performed on the test results of first-order natural frequency and first-order amplitude_max to determine the significance of crack depth, crack height, and bladed disk speed on the test results.

The results of ANOVA are shown in Table 4. The crack depth, crack height and bladed disk rotational speed have no significant effect on the first-order natural frequency, and the crack depth and bladed disk rotational speed also have no significant effect on the first-order amplitude_max, and the crack height has a significant effect on the first-order amplitude_max. Therefore, the height of the crack is the main factor affecting the vibration characteristics of the bladed disk, which is basically consistent with the results of the extreme difference analysis.

Table 4Analysis of variance results

	Source of variance	Sum of squares of deviations	$f$	Mean square	$F$	$P$	Conspicuousness
First-order natural frequency	$D$	536.63	2.00	268.32	1.40	0.42	–
	$H$	1219.25	2.00	609.62	3.18	0.24	–
	$N$	484.86	2.00	242.43	1.27	0.44	–
	Error	383.10	2.00	191.55	–	–
First-order amplitude_max	$H$	9.98	2	4.99	81.43	0.012	*
First-order amplitude_max	Overall error	0.37	6	0.06	–	–	–
*indicates the importance of the first level

5. Effect of crack distribution on vibration characteristics of multi-crack bladed disk system

In engineering practice, cracks often appear on several blades of the bladed disk structure at the same time. For this reason, this section investigates the effect of the distribution of blades containing two cracks and three cracks on the vibration characteristics of the detuned bladed disk structure. Section 3 shows that when the crack depth is 15 mm and the crack height is 20 mm, the most obvious effect is on the vibration characteristics of the bladed disk. In turn, the rotating bladed disk vibration characteristics will continuously differ from the static bladed disk as the bladed disk speed increases. Therefore, in this section, the static and dynamic (4000 r/min) vibration characteristics of the multi-crack bladed disk will be studied under this condition, respectively.

5.1. Effect on two-crack bladed disk

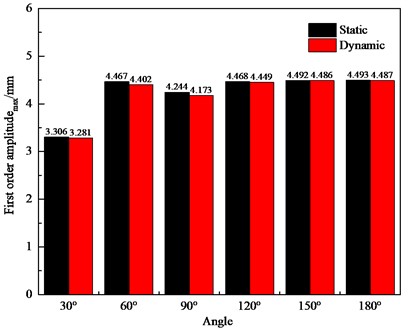
There are various cases of the distribution form of two crack-containing blades, and the numerical simulations were performed for the two cracked blades with angles of 30°, 60°, 90°, 120°, 150°, and 180°, respectively, and the first twelve orders of the natural frequencies and the first-order amplitude_max of the bladed disk under static and dynamic conditions were obtained, as shown in Figs. 7 and 8, respectively. It is found that the double-crack bladed disk system has a significantly lower natural frequency in the first two orders compared with the harmonic bladed disk system, and there is no significant change in the natural frequency in the third order or after the third order. When the two cracked blades are in adjacent positions, the first-order natural frequency of the detuned bladed disk structure is the smallest and the first-order amplitude_max is the largest; while when the two cracked blades are 180° apart, the first-order natural frequency of the detuned bladed disk structure is the largest and the first-order amplitude_max is the smallest, which is related to the symmetry of the crack distribution. Therefore, the distribution of cracked blades has some influence on the vibration characteristics of the detuned bladed disk structure. Compared with the single-crack bladed disk, the single-crack bladed disk affects the first-order natural frequency, while the double-crack bladed disk affects the first two orders of natural frequency; the bladed disk system with a double-crack bladed disk is basically equal to the single-crack bladed disk system in terms of first-order amplitude_maxand even significantly lower than the single-crack bladed disk system when two cracked blades are adjacent to each other.

Fig. 7Different order natural frequencies of bladed disks with different crack distribution angles (two cracks)

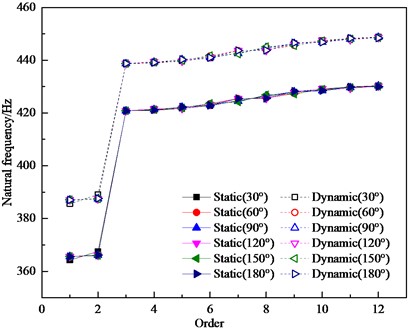
Fig. 8First order amplitudesmax of bladed disks with different crack distribution angles (two cracks)

5.2. Effect on three-crack bladed disk

Since the crack distribution of the three-crack bladed disk system is complicated, the blades are numbered. The crack distribution is shown in Table 5, where the longitudinal serial number represents the number of crack-free blades between the first and second cracked blades and the transverse serial number represents the number of crack-free blades between the second and third cracked blades.

Table 5Crack distribution of three-crack bladed disk

Number	0	1	2	3	4
0	(0, 0)	(0, 1)	(0, 2)	(0, 3)	(0, 4)
1		(1, 1)	(1, 2)	(1, 3)
2			(2, 2)	(2, 3)
3				(3, 3)

The first twelve orders of natural frequencies and the first-order amplitude_max of the bladed disk under static and dynamic conditions were obtained by numerical simulation for the above three-crack bladed disk system with different distribution conditions, as shown in Figs. 9 and 10, respectively.

Fig. 9Different order natural frequencies of bladed disks with different crack distribution angles (three cracks)

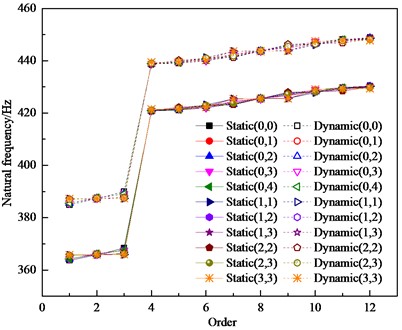
Fig. 10First order amplitudesmax of bladed disks with different crack distribution locations (three cracks)

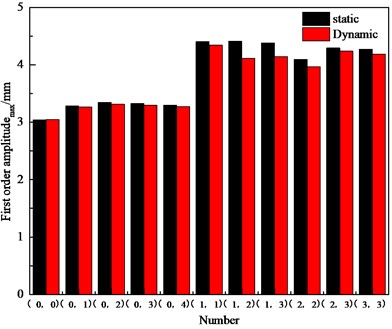
Similar to the double-crack bladed disk system, the first three orders of natural frequency of the three-crack bladed disk system are significantly lower compared with the harmonic bladed disk system, and there is no significant change in the fourth order or the natural frequency after the fourth order. Similarly, when the three cracked blades are in adjacent positions, the first-order natural frequency of the detuned bladed disk structure is the smallest and the first-order amplitude_max is the largest. When the cracked blades are not adjacent, the first order amplitude_max of the bladed disk system is significantly higher than that of the bladed disk system with adjacent cracked blades. Compared with the single-crack bladed disk system, the first-order amplitudes_max of the three-crack bladed disk system and the single-crack bladed disk system are basically equal when the cracked blades of the three-crack disk system are not adjacent to each other; when the three-crack bladed disk system has more than two adjacent cracked blades, the first-order amplitudes_max are significantly lower than those of the single-crack bladed disk system.

6. Conclusions

The infuence on the vibration characteristics of the cracked bladed disk system was studied, and some conclusions could be drawn as follows:

1) The dynamic natural frequency of the cracked bladed disk and harmonic bladed disk is higher than their static natural frequency, with the natural frequency increasing as the speed increases. This effect primarily results from the centrifugal force increasing the rigidity of the bladed disk and thereby affecting its natural frequency.

2) Different modes of the harmonic bladed disk exhibit uniform amplitude distribution across each blade, while the amplitude distribution of the cracked bladed disk in the first-order mode is highest on the cracked blade and significantly exceeds the amplitudes on the other blades. The impact of the vibration characteristics of the cracked bladed disk becomes increasingly apparent as the crack depth deepens.

3) Regarding the single-crack bladed disk system, the influence of the crack on the bladed disk’s natural frequency decreases as the distance between the crack and the blade root increases. When the crack height reaches 100 mm, its effect on the inherent frequency of the bladed disk is almost negligible. The maximum amplitudes of the dynamic and static first-order modes of the cracked bladed disk are virtually identical. The impact of the crack on the first-order amplitudes_max of the bladed disk beneath the height of 1/2 the blade height is apparent, while its impact above this threshold gradually diminishes with increasing crack height, ultimately converging to 0.

4) Crack depth, crack height, and bladed disk speed do not significantly affect the natural frequency of the single-crack bladed disk system, whereas crack height exerts a considerable influence on the first-order amplitude_max of the bladed disk system.

5) In the scope of this study, the number of cracked blades corresponds to the order of the affected natural frequency. When the cracked blades are all adjacent to each other, the first-order natural frequency of the detuned bladed disk structure is the smallest and the first-order amplitude_max is the largest; when there are adjacent cracked blades in the cracked disk system, the first-order amplitude_max is significantly lower than that of the single-crack bladed disk system.

The results of this study lay the foundation for blade health monitoring and fault prediction, but they are limited to situations without excitation force. Future research will include experimental studies on the frequency response changes and tip displacement response characteristics of multi-cracked blades under excitation forces.

References

D. Nowell, “Prediction of fatigue performance in gas turbine blades after foreign object damage,” International Journal of Fatigue, Vol. 25, No. 9-11, pp. 963–969, Sep. 2003, https://doi.org/10.1016/s0142-1123(03)00160-9

Publisher
H. Xu, Z. Chen, Y. Yang, L. Tao, and X. Chen, “Effects of crack on vibration characteristics of mistuned rotated blades,” Shock and Vibration, Vol. 2017, pp. 1–18, 2017, https://doi.org/10.1155/2017/1785759

Publisher
J. P. Chung and H. H. Yoo, “Blade fault diagnosis using Mahalanobis distance,” Journal of Mechanical Science and Technology, Vol. 35, No. 4, pp. 1377–1385, Apr. 2021, https://doi.org/10.1007/s12206-021-0304-y

Publisher
Y.-J. Chiu and S.-C. Huang, “The influence of a cracked blade on rotor’s free vibration,” Journal of Vibration and Acoustics, Vol. 130, No. 5, Oct. 2008, https://doi.org/10.1115/1.2948381

Publisher
C. Zhao, J. Zeng, H. Ma, K. Ni, and B. Wen, “Dynamic analysis of cracked rotating blade using cracked beam element,” Results in Physics, Vol. 19, p. 103360, Dec. 2020, https://doi.org/10.1016/j.rinp.2020.103360

Publisher
L. Yang, Z. Mao, S. Wu, X. Chen, and R. Yan, “Nonlinear dynamic behavior of rotating blade with breathing crack,” Frontiers of Mechanical Engineering, Vol. 16, No. 1, pp. 196–220, Mar. 2021, https://doi.org/10.1007/s11465-020-0609-z

Publisher
G. Xu, L. Liang, J. Li, H. Mei, H. Li, and Y. Liu, “Study on influence of crack on the blade status using FBGs,” Photonic Sensors, Vol. 8, No. 1, pp. 63–69, Mar. 2018, https://doi.org/10.1007/s13320-017-0451-z

Publisher
J. Zeng, K. Chen, H. Ma, T. Duan, and B. Wen, “Vibration response analysis of a cracked rotating compressor blade during run-up process,” Mechanical Systems and Signal Processing, Vol. 118, pp. 568–583, Mar. 2019, https://doi.org/10.1016/j.ymssp.2018.09.008

Publisher
C. W. Li, Z. Miao, B. Y. Yang, Z. P. Zhang, and L. Y. Zhang, “Study on foreign object damage law of titanium alloy blade of an aero-engine impacted by sandstone,” Strength of Materials, Vol. 54, No. 2, pp. 292–301, Mar. 2022, https://doi.org/10.1007/s11223-022-00405-3

Publisher
H. Arvin, M. Sadighi, and A. R. Ohadi, “A numerical study of free and forced vibration of composite sandwich beam with viscoelastic core,” Composite Structures, Vol. 92, No. 4, pp. 996–1008, Mar. 2010, https://doi.org/10.1016/j.compstruct.2009.09.047

Publisher
M. Petyt, “The vibration characteristics of a tensioned plate containing a fatigue crack,” Journal of Sound and Vibration, Vol. 8, No. 3, pp. 377–389, Nov. 1968, https://doi.org/10.1016/0022-460x(68)90244-7

Publisher
C.-C. Ma and C.-H. Huang, “Experimental and numerical analysis of vibrating cracked plates at resonant frequencies,” Experimental Mechanics, Vol. 41, No. 1, pp. 8–18, Mar. 2001, https://doi.org/10.1007/bf02323099

Publisher
B.-W. Huang and J.-H. Kuang, “Variation in the stability of a rotating blade disk with a local crack defect,” Journal of Sound and Vibration, Vol. 294, No. 3, pp. 486–502, Jun. 2006, https://doi.org/10.1016/j.jsv.2005.11.028

Publisher
C. Lien-Wen and C. Chiung-Lu, “Vibration and stability of cracked thick rotating blades,” Computers and Structures, Vol. 28, No. 1, pp. 67–74, Jan. 1988, https://doi.org/10.1016/0045-7949(88)90093-4

Publisher
Hou and J. F., “Cracking-induced mistuning in bladed disks,” AIAA Journal, Vol. 44, pp. 2542–2546, 2006.

Publisher
S. Loutridis, E. Douka, and L. J. Hadjileontiadis, “Forced vibration behaviour and crack detection of cracked beams using instantaneous frequency,” NDT and E International, Vol. 38, No. 5, pp. 411–419, Jul. 2005, https://doi.org/10.1016/j.ndteint.2004.11.004

Publisher
X. Fang, J. Tang, E. Jordan, and K. D. Murphy, “Crack induced vibration localization in simplified bladed-disk structures,” Journal of Sound and Vibration, Vol. 291, No. 1-2, pp. 395–418, Mar. 2006, https://doi.org/10.1016/j.jsv.2005.06.020

Publisher
A. Saito, M. P. Castanier, and C. Pierre, “Estimation and veering analysis of nonlinear resonant frequencies of cracked plates,” Journal of Sound and Vibration, Vol. 326, No. 3-5, pp. 725–739, Oct. 2009, https://doi.org/10.1016/j.jsv.2009.05.009

Publisher
C. Liu and D. Jiang, “Crack modeling of rotating blades with cracked hexahedral finite element method,” Mechanical Systems and Signal Processing, Vol. 46, No. 2, pp. 406–423, Jun. 2014, https://doi.org/10.1016/j.ymssp.2014.01.007

Publisher
L.-H. Yang, Z. Mao, S.-M. Wu, X.-F. Chen, and R.-Q. Yan, “Steady-state coupling vibration analysis of shaft-disk-blade system with blade crack,” Nonlinear Dynamics, Vol. 105, No. 1, pp. 61–98, Jul. 2021, https://doi.org/10.1007/s11071-021-06645-3

Publisher
B.-W. Huang, “Effect of number of blades and distribution of cracks on vibration localization in a cracked pre-twisted blade system,” International Journal of Mechanical Sciences, Vol. 48, No. 1, pp. 1–10, Jan. 2006, https://doi.org/10.1016/j.ijmecsci.2005.09.016

Publisher
D. J. Ewins, “A study of resonance coincidence in bladed discs,” Journal of Mechanical Engineering Science, Vol. 12, No. 5, pp. 305–312, Oct. 1970, https://doi.org/10.1243/jmes_jour_1970_012_055_02

Publisher
C. J. Roy and W. L. Oberkampf, “A comprehensive framework for verification, validation, and uncertainty quantification in scientific computing,” Computer Methods in Applied Mechanics and Engineering, Vol. 200, No. 25-28, pp. 2131–2144, Jun. 2011, https://doi.org/10.1016/j.cma.2011.03.016

Publisher
W. Kim and J. Chung, “Free non-linear vibration of a rotating thin ring with the in-plane and out-of-plane motions,” Journal of Sound and Vibration, Vol. 258, No. 1, pp. 167–178, Nov. 2002, https://doi.org/10.1006/jsvi.2002.5104

Publisher
X. Wu and R. G. Parker, “Vibration of rings on a general elastic foundation,” Journal of Sound and Vibration, Vol. 295, No. 1-2, pp. 194–213, Aug. 2006, https://doi.org/10.1016/j.jsv.2006.01.007

Publisher
J. H. Kuang and B. W. Huang, “Mode localization of a cracked blade disk,” Journal of Engineering for Gas Turbines and Power, Vol. 121, No. 2, pp. 335–341, Apr. 1999, https://doi.org/10.1115/1.2817125

Publisher
J. H. Kuang and B. W. Huang, “The effect of blade crack on mode localization in rotating bladed disks,” Journal of Sound and Vibration, Vol. 227, No. 1, pp. 85–103, Oct. 1999, https://doi.org/10.1006/jsvi.1999.2329

Publisher
Tybout A. et al., “Analysis of variance,” Journal of Consumer Psychology, Vol. 10, No. 1-2, pp. 5–35, 2001.

Publisher

About this article

Received

20 April 2023

Accepted

12 June 2023

Published

01 August 2023

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/jve.2023.23337

Keywords

bladed disk system

crack depth

crack distribution

orthogonal test method

natural frequency

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Conceptualization: C. Pan and Y. D. Dai; Methodology: C. Pan; Software: C. Pan; Writing-Original Draft Preparation: C. Pan; Writing-Review and Editing: Y. D. Dai and Y. C. Li; Funding acquisition, Y. D. Dai and Y. C. Li.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2020 12 04

Vibration reduction optimization for mistuned bladed disk based on reduced order modeling technique

Hongyuan Zhang, Huiqun Yuan, Hongyun Sun

Research article

2019 09 30

Forced response characteristics of random mistuned blade disk based on weibull distribution and monte carlo simulation

Hongyuan Zhang, Huiqun Yuan, Hongyun Sun

Research article

2018 11 15

Vibration characteristics analysis of mistuned bladed disk system based on mobile interface prestressed CMS super-element method

Liang Zhang, Yuan He, Huiqun Yuan, Xin Li

Research article

2017 10 21

The operation modal analysis of the structure crack fault diagnosis based on pseudo-successive data

Chen Xiaoguang, Yang Jinpeng, Sheng Xi, An Zhengang, Li Bing

C. Pan, Y. Dai, and Y. Li, “Simulation study of crack parameters’ effects on the vibration characteristics of a bladed disk system,” Journal of Vibroengineering, Vol. 25, No. 7, pp. 1273–1284, Aug. 2023, https://doi.org/10.21595/jve.2023.23337

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2023.23337
UR  - https://doi.org/10.21595/jve.2023.23337
TI  - Simulation study of crack parameters’ effects on the vibration characteristics of a bladed disk system
T2  - Journal of Vibroengineering
AU  - Pan, Chuang
AU  - Dai, Yuande
AU  - Li, Yaocheng
PY  - 2023
DA  - 2023/08/01
PB  - JVE International Ltd.
SP  - 1273-1284
VL  - 25
IS  - 7
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

 @article{Pan_2023, title={Simulation study of crack parameters’ effects on the vibration characteristics of a bladed disk system}, volume={25}, ISSN={2538-8460}, url={https://doi.org/10.21595/jve.2023.23337}, DOI={10.21595/jve.2023.23337}, number={7}, journal={Journal of Vibroengineering}, publisher={JVE International Ltd.}, author={Pan, Chuang and Dai, Yuande and Li, Yaocheng}, year={2023}, month=aug, pages={1273–1284} }

Copy Bibtex

Copied to clipboard!

[1]C. Pan, Y. Dai, and Y. Li, “Simulation study of crack parameters’ effects on the vibration characteristics of a bladed disk system,” Journal of Vibroengineering, vol. 25, no. 7, pp. 1273–1284, Aug. 2023, doi: 10.21595/jve.2023.23337.

Copy IEEE

Copied to clipboard!

Pan, Chuang, Yuande Dai, and Yaocheng Li. “Simulation Study of Crack Parameters’ Effects on the Vibration Characteristics of a Bladed Disk System.” Journal of Vibroengineering 25, no. 7 (August 1, 2023): 1273–84. https://doi.org/10.21595/jve.2023.23337.

Copy Chicago

Copied to clipboard!

Simulation study of crack parameters’ effects on the vibration characteristics of a bladed disk system

Abstract

Highlights

1. Introduction

2. Modeling

3. Effect on the vibration characteristics of a single-crack bladed disk system

3.1. Effect of single-crack depth

3.2. Effect of single-crack height

4. Dynamic vibration characteristics of a single-crack bladed disk

4.1. Range analysis

4.2. Analysis of variance

5. Effect of crack distribution on vibration characteristics of multi-crack bladed disk system

5.1. Effect on two-crack bladed disk

5.2. Effect on three-crack bladed disk

6. Conclusions

References

About this article

Related Articles