Abstract
In the dynamic processes taking place in manipulators and robots, impact interactions play an important role. Among them two sided impacts are important. In this paper investigation of dynamic regimes of a system with two impacting surfaces, one of which is in the position of equilibrium is performed. Dynamics in steady state regime for typical parameters of the investigated system having one degree of freedom is investigated. Displacements as functions of time as well as velocities as functions of time for various positions of the impacting surface are presented. Non symmetric impacts enable to reduce the dimensions of the vibrator and to achieve increase of effectiveness of useful impacts of a manipulator. Investigations of the conservative system as well as of the system with forced harmonic excitation are performed.
1. Introduction
In the dynamic processes taking place in manipulators and robots, impact interactions play an important role. Among them two sided impacts are important. In this paper investigation of dynamic regimes of a system with two impacting surfaces, one of which is in the position of equilibrium is performed. Such systems represent the case of a pipe robot. Also, they represent systems attached to a mass with a self-stopping mechanism in precise robots used for vibrational transportation. Dynamics in steady state regime for typical parameters of the investigated system having one degree of freedom is investigated.
Similar problems are investigated in the field of physics of nonlinear systems. In those problems chaotic dynamics and bifurcations are observed. This paper is not devoted to chaotic dynamics and bifurcations as well as physics of nonlinear systems, but to the investigation of recommended for practical applications in engineering and robotics regimes of motion.
Displacements as functions of time as well as velocities as functions of time for various positions of the impacting surface are presented. Investigations of the conservative system as well as of the system with forced harmonic excitation are performed. Investigation of dynamics for various frequencies of excitation enables to determine optimal frequency of excitation.
Resonances in nonlinear systems are described in [1]. Systems with impacts are investigated in [2]. Stabilization of dynamical systems is presented in [3]. Impacts in vibrating systems are investigated in [4]. Periodic orbits are analyzed in [5]. Vibro-impact energy sink is investigated in [6]. Particle impact with a wall is presented in [7]. Frequencies of a multibody system are analyzed in [8]. Pendulum and its dynamics are investigated in [9]. Piecewise linearity is analyzed in [10]. Resonant zones are investigated in [11]. Sommerfeld effect is presented in [12]. Isolated resonances are investigated in [13].
A number of contemporary publications are devoted to the bouncing ball problem. Bouncing ball model is analyzed in [14]. Bouncing ball system with nonlinear limiter is investigated in [15]. Stability of bouncing ball system is analyzed in [16].
Applications in robotics and manufacturing are described in a number of books and papers. Contemporary problems in the design of robots are described in [17]. Positioning system with high resolution in manufacturing technology is investigated in [18]. Automatic positioning stage is analyzed in [19]. Piezo-driven stage in integrated manufacturing is investigated in [20]. Precision positioning stage is analyzed in [21].
Basic theory of vibro-impact systems is presented in [22]. Dynamics and impacts in transmissions are investigated in [23]. Vibrations in elements of robots are analyzed in [24]. This paper is the continuation of investigations presented there.
First the model of the investigated system is described. Then the results of calculation of impact interactions are presented. Graphical results for recommended parameters of the system are described in detail.
2. Model of the system with two sided impacts
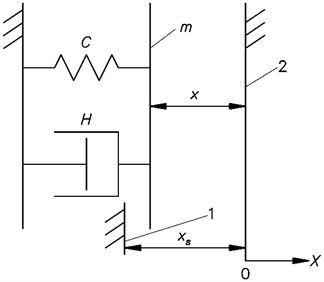
The investigated system is shown in Fig. 1. Equations of dynamics of the system shown in Fig. 1 are the following ones:
Fig. 1Model of the system with two sided impacts: m is the mass of the investigated system, H is the coefficient of viscous damping, C is the coefficient of stiffness, x is the displacement of the mass m, 1 and 2 denote the impacting surfaces, xs is the position of the impacting surface 1, while it is assumed that the position of the impacting surface 2 is the position of equilibrium and is equal to zero
Motion is divided into two intervals according to the time:
when:
when:
Here as usual it is assumed that impacts take place in a moment according to the time, that is at t-0 velocity before impact is denoted as ˙x- and at t+0 velocity after impact is denoted as ˙x+.
About the positions x=0 and x=xs separately series of one directional impacts takes place, that is there exist:
Equations of dynamics of the system are Eq. (1)-(5). By introducing the changes in the previous equations with the notations:
'=ddτ,x'=p˙x,x''=p2¨x,'=ddτ,
where on the basis of Eq. (6) by taking into account the Eqs. (2-5) it is obtained:
Motions according to the non-dimensional time τ:
where:
τ=τj,x=xs,
τ=τl,x=0,
when:
3. Investigation of dynamics of the conservative system
Conservative system takes place when:
and the equations of the system according to the previous equations are the following ones:
Motion according to the non-dimensional time takes place according to the two intervals:
where:
τ=0-0,x'-0>0,
τ=0+0,x'+0=-x'-0<0,
where:
τ=τ1-0,x'-1<0,
τ=τ1+0,x'+1=-x'-1>0,
where:
τ=τ2-0,x'-2>0,
τ=τ2+0,x'+2=-x'-2<0.
In the interval τ∈(0,τ1) motion according to the Eq. (12) is the following one:
where C0 and D0 are found from the initial conditions of motion according to the Eq. (14):
and at the end of the interval at τ=τ1-0:
and at τ=τ1+0:
In the interval τ∈(τ1,τ2) according to the Eq. (12), (13) motion takes place:
where constant quantities are found from the initial conditions of motion in the interval:
and by substituting into the Eq. (21) it is obtained:
At the end of the interval τ=τ2=2τ1 it is obtained:
From the first equation of the Eq. (19) τ1 is determined, that is xsx0'-=-sinτ1 is valid only at the conditions of existence of one impact to the support 1 and one impact to the support 2 in the period of motion according to the time, that is:
Non dimensional period ˉT and frequency ˉω of existing motions of the conservative system are:
3.1. Investigation of dynamics of the conservative system for various initial velocities
Calculations from zero initial displacement and for a given position of the impact surface are performed:
Results for various initial velocities were obtained. Further they are presented for two typical initial velocities. Two periods of motion are shown in the figures.
Results of investigation of dynamics of the system with two sided impacts for:
are presented in Fig. 2. It is seen that minimum value of displacement is approximately equal to the position of the lower impact surface, that is for larger (smaller in absolute value) initial velocities impacts to the lower surface do not take place, while for smaller (larger in absolute value) initial velocities impacts to the lower surface take place. Results of investigation of dynamics of the system with two sided impacts for:
are presented in Fig. 3. This is a typical regime of motion when impacts to both surfaces take place. Period of vibrations as function of the initial velocity is represented in Fig. 4.
Fig. 2Dynamics of the system with two sided impacts for x'0=-0.75
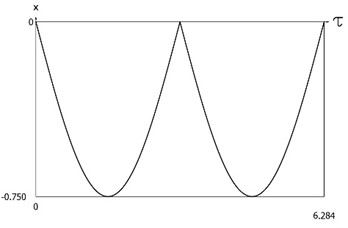
a)x=x(τ)
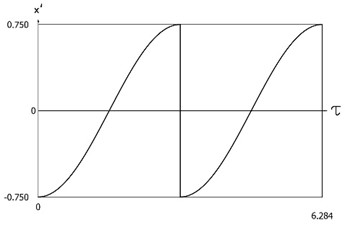
b)x'=x'(τ)
Amplitudes of the first three harmonics of displacement as functions of period of vibrations are presented in Fig. 5. Amplitudes of the first three harmonics of velocity as functions of period of vibrations are presented in Fig. 6. In both figures vertical lines correspond to motions when impacts to the lower surface do not take place, while substantial influence of impacts to the lower surface to the period of vibrations is observed. Constant part and amplitudes of the first three harmonics of displacement as functions of frequency are presented in Fig. 7. Constant part and amplitudes of the first three harmonics of velocity as functions of frequency are presented in Fig. 8. In both figures vertical lines correspond to motions when impacts to the lower surface do not take place, while substantial influence of impacts to the lower surface to the frequencies of vibrations is observed. The obtained graphical representations enable to understand the behavior of the investigated conservative vibro-impact system.
Fig. 3Dynamics of the system with two sided impacts for x'0=-1
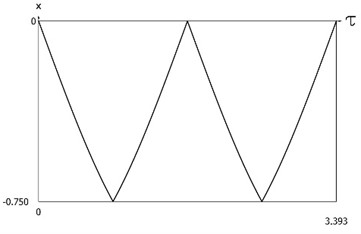
a)x=x(τ)
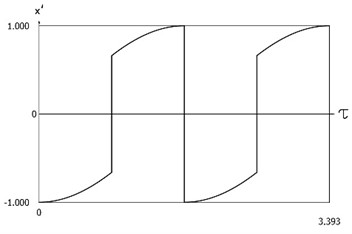
b)x'=x'(τ)
Fig. 4Period of vibrations as function of the initial velocity
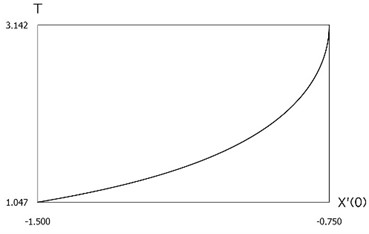
Fig. 5Amplitude of displacement – period according to τ characteristics
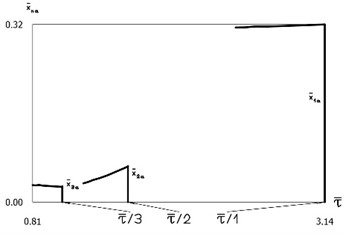
Fig. 6Amplitude of velocity – period according to τ characteristics
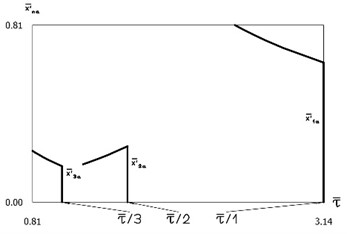
Fig. 7Amplitude of displacement – frequency characteristics
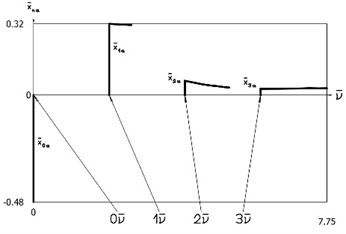
Fig. 8Amplitude of velocity – frequency characteristics
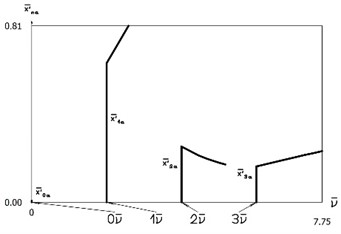
3.2. Investigation of dynamics of the conservative system for various positions of the impact surface
Calculations from the following initial conditions are performed:
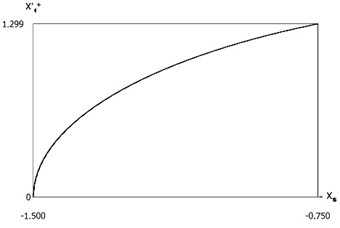
Results for various positions of the impact surface were obtained. Variations of velocities before impact as functions of the position of the impacting surface for the first impacting surface are presented in Fig. 9. Variations of velocities after impact as functions of the position of the impacting surface for the first impacting surface are presented in Fig. 10. Velocities before impact as functions of the position of the impacting surface for the second impacting surface are approximately equal to x'-2=1.5. Velocities after impact as functions of the position of the impacting surface for the second impacting surface are approximately equal to x'+2=-1.5. The obtained graphical representations enable to understand the behavior of the investigated vibro-impact system.
Fig. 9Variations of velocities before impact as functions of the position of the impacting surface for the first impacting surface
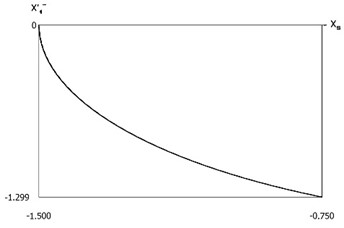
Fig. 10Variations of velocities after impact as functions of the position of the impacting surface for the first impacting surface
4. Investigation of impact interactions in the system with two sided impacts for forced harmonic excitations
Further the exciting force is denoted as:
Calculations from zero initial conditions are performed:
Two periods of steady state motions are shown in the figures.
4.1. Investigation of dynamics of the system for various coefficients of restitution
Typical parameters of the investigated system with two sided impacts were assumed:
Results for various values of coefficient of restitution were obtained. Further they are presented for three typical values of coefficient of restitution.
Results of investigation of dynamics of the system with two sided impacts in steady state regime of motion for:
are presented in Fig. 11. In a period of vibrations one impact to the lower surface and two impacts to the upper surface are observed. Results of investigation of dynamics of the system with two sided impacts in steady state regime of motion for:
are presented in Fig. 12. In a period of vibrations one impact to the lower surface and three impacts to the upper surface are observed. Results of investigation of dynamics of the system with two sided impacts in steady state regime of motion for:
are presented in Fig. 13. In a period of vibrations one impact to the lower surface and a number of impacts to the upper surface are observed. From the presented results the influence of the value of coefficient of restitution to the behavior of the investigated system is observed.
Fig. 11Dynamics of the system with two sided impacts in steady state regime of motion for ν=1, f=-1, h=0.1, xs=-1, R=0.9
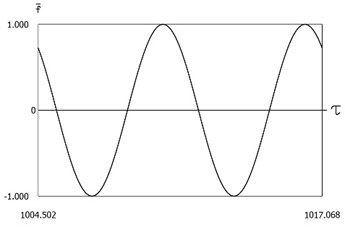
a)ˉf=ˉf(τ)
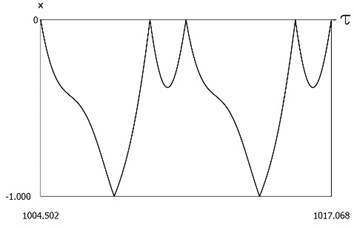
b)x=x(τ)
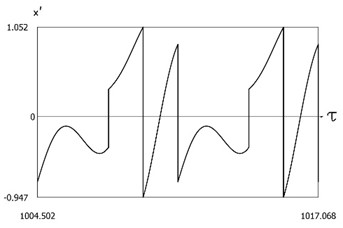
c)x'=x'(τ)
Fig. 12Dynamics of the system with two sided impacts in steady state regime of motion for ν=1, f=-1, h=0.1, xs=-1, R=0.7
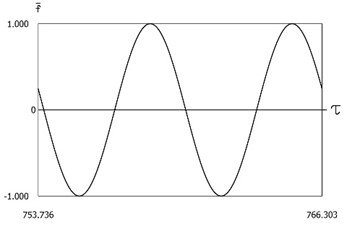
a)ˉf=ˉf(τ)
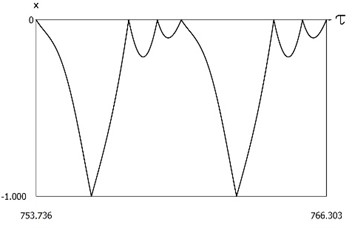
b)x=x(τ)
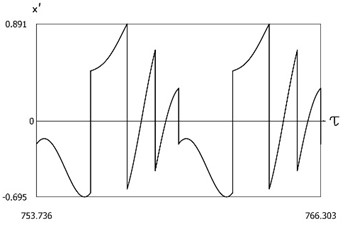
c)x'=x'(τ)
Fig. 13Dynamics of the system with two sided impacts in steady state regime of motion for ν=1, f=-1, h=0.1, xs=-1, R=0.5
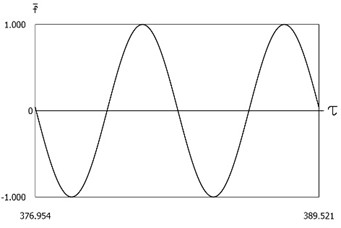
a)ˉf=ˉf(τ)
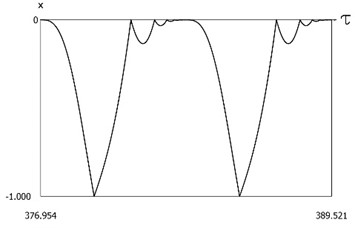
b)x=x(τ)
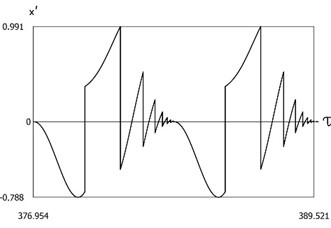
c)x'=x'(τ)
4.2. Investigation of dynamics of the system for various positions of the impact surface
Typical parameters of the investigated system with two sided impacts were assumed:
Results for various positions of the impact surface were obtained. Further they are presented for four typical positions of the impact surface.
Results of investigation of dynamics of the system with two sided impacts in steady state regime of motion for:
are presented in Fig. 14. The characteristic feature of this regime of motion is that in the period of steady state motion there is one impact to the lower surface and several impacts to the upper surface. Results of investigation of dynamics of the system with two sided impacts in steady state regime of motion for:
are presented in Fig. 15.
Fig. 14Dynamics of the system with two sided impacts in steady state regime of motion for ν=1, f=-1, h=0.1, R=0.7, xs=-0.75
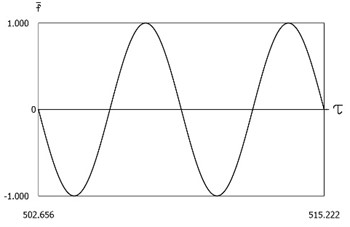
a)ˉf=ˉf(τ)
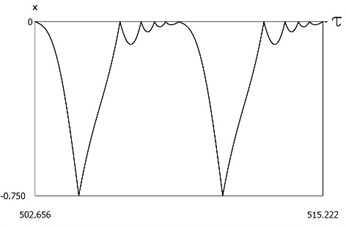
b)x=x(τ)
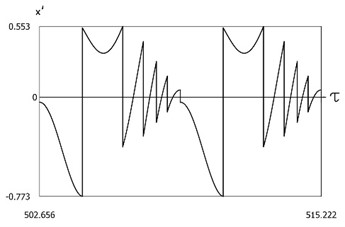
c)x'=x'(τ)
Fig. 15Dynamics of the system with two sided impacts in steady state regime of motion for ν=1, f=-1, h=0.1, R=0.7, xs=-1
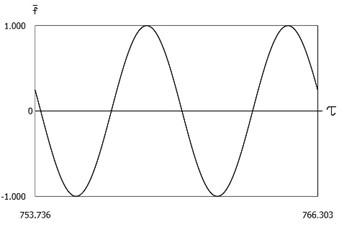
a)ˉf=ˉf(τ)
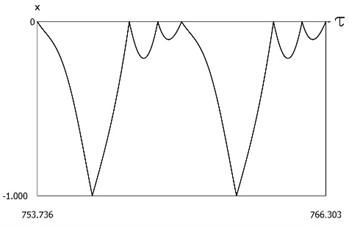
b)x=x(τ)
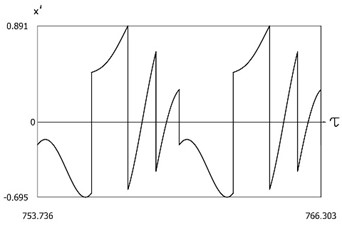
c)x'=x'(τ)
The characteristic feature of this regime of motion is that in the period of steady state motion there is one impact to the lower surface and several impacts to the upper surface, but the number of impacts to the upper surface has decreased when compared with the previous case. Results of investigation of dynamics of the system with two sided impacts in steady state regime of motion for:
are presented in Fig. 16. The characteristic feature of this regime of motion is that one period of steady state motion corresponds to two periods of the exciting force. Results of investigation of dynamics of the system with two sided impacts in steady state regime of motion for:
are presented in Fig. 17. The characteristic feature of this regime of motion is that in the steady state regime of motion impacts to the lower surface do not take place.
Fig. 16Dynamics of the system with two sided impacts in steady state regime of motion for ν=1, f=-1, h=0.1, R=0.7, xs=-1.25
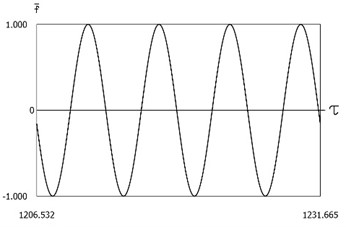
a)ˉf=ˉf(τ)
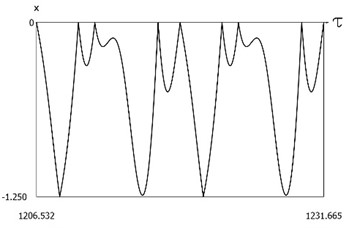
b)x=x(τ)
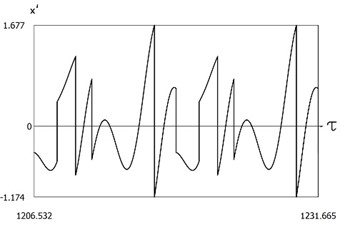
c)x'=x'(τ)
Fig. 17Dynamics of the system with two sided impacts in steady state regime of motion for ν=1, f=-1, h=0.1, R=0.7, xs=-1.5
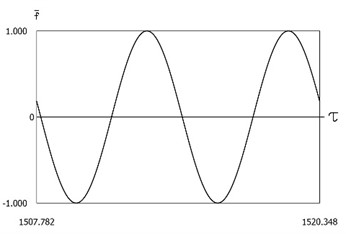
a)ˉf=ˉf(τ)
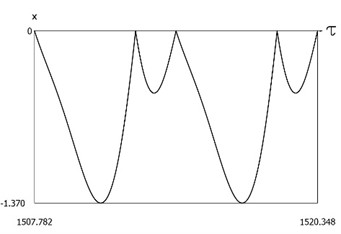
b)x=x(τ)
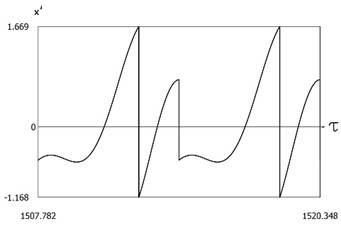
c)x'=x'(τ)
5. Investigation of steady state dynamics for various frequencies of excitation
Typical parameters of the investigated system with two sided impacts were assumed:
Results of investigation of dynamics in steady state regime of motion for:
are presented in Fig. 18. In this case impacts to the first surface do not take place. Results of investigation of dynamics in steady state regime of motion for:
are presented in Fig. 19. Results of investigation of dynamics in steady state regime of motion for:
are presented in Fig. 20. From the obtained results optimal frequency of excitation is determined.
Fig. 18Dynamics in steady state regime for f=-1, h=0.1, R=0.7, xs=-1.5
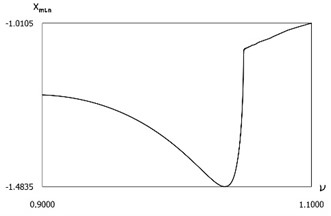
a) Minimum displacements
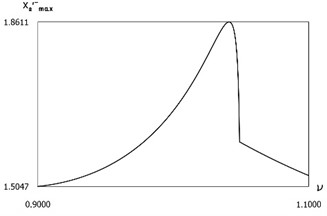
b) Maximum velocities before impact to the second surface
Fig. 19Dynamics in steady state regime for f=-1, h=0.1, R=0.7, xs=-1.4
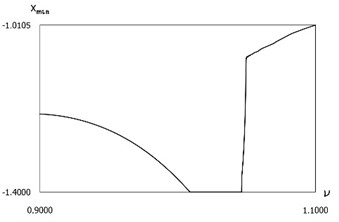
a) Minimum displacements
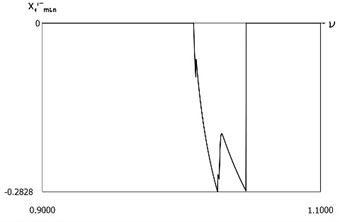
b) Minimum velocities before impact to the first surface
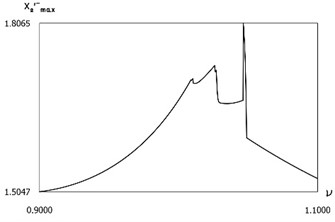
c) Maximum velocities before impact to the second surface
Fig. 20Dynamics in steady state regime for f=-1, h=0.1, R=0.7, xs=-1.3
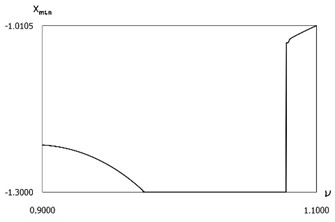
a) Minimum displacements
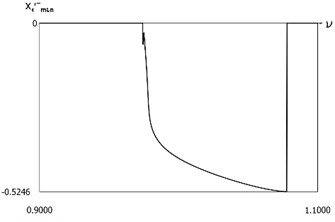
b) Minimum velocities before impact to the first surface
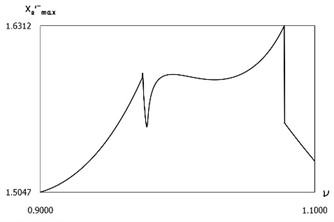
c) Maximum velocities before impact to the second surface
6. Conclusions
In the dynamic processes taking place in manipulators and robots, impact interactions play an important role, among them two sided impacts are important. First the model of the investigated system is described. Then the results of calculation of impact interactions are presented. Graphical results for recommended parameters of the system are described in detail.
Dynamics in steady state regime for typical parameters of the investigated system having one degree of freedom is investigated. Displacements as functions of time as well as velocities as functions of time for various positions of the impacting surface are presented. The characteristic feature of the first regime of motion is that in the period of steady state motion there is one impact to the lower surface and several impacts to the upper surface. The characteristic feature of the second regime of motion is that in the period of steady state motion there is one impact to the lower surface and several impacts to the upper surface, but the number of impacts to the upper surface has decreased when compared with the previous case. The characteristic feature of the third regime of motion is that one period of steady state motion corresponds to two periods of the exciting force. The characteristic feature of the fourth regime of motion is that in the steady state regime of motion impacts to the lower surface do not take place. Investigation of dynamics for various frequencies of excitation enables to determine optimal frequency of excitation. Proposed vibrator with non-symmetric impacts enables to reduce the dimensions of the system and to achieve increase of effectiveness of useful impacts of a manipulator. The results are used in the process of design of elements of robots in which impact interactions take place.
References
-
W. V. Wedig, “New resonances and velocity jumps in nonlinear road-vehicle dynamics,” Procedia IUTAM, Vol. 19, pp. 209–218, 2016, https://doi.org/10.1016/j.piutam.2016.03.027
-
T. Li, E. Gourc, S. Seguy, and A. Berlioz, “Dynamics of two vibro-impact nonlinear energy sinks in parallel under periodic and transient excitations,” International Journal of Non-Linear Mechanics, Vol. 90, pp. 100–110, Apr. 2017, https://doi.org/10.1016/j.ijnonlinmec.2017.01.010
-
V. A. Zaitsev, “Global asymptotic stabilization of periodic nonlinear systems with stable free dynamics,” Systems and Control Letters, Vol. 91, pp. 7–13, May 2016, https://doi.org/10.1016/j.sysconle.2016.01.004
-
H. Dankowicz and E. Fotsch, “On the analysis of chatter in mechanical systems with impacts,” Procedia IUTAM, Vol. 20, pp. 18–25, 2017, https://doi.org/10.1016/j.piutam.2017.03.004
-
S. Spedicato and G. Notarstefano, “An optimal control approach to the design of periodic orbits for mechanical systems with impacts,” Nonlinear Analysis: Hybrid Systems, Vol. 23, pp. 111–121, Feb. 2017, https://doi.org/10.1016/j.nahs.2016.08.009
-
L. Wenke, N. Wierschem, Xinhui Li, and Tiejun Yang, “On the energy transfer mechanism of the single-sided vibro-impact nonlinear energy sink,” Journal of Sound and Vibration, Vol. 437, pp. 166–179, 2018.
-
J. S. Marshall, “Modeling and sensitivity analysis of particle impact with a wall with integrated damping mechanisms,” Powder Technology, Vol. 339, pp. 17–24, Nov. 2018, https://doi.org/10.1016/j.powtec.2018.07.097
-
E. Salahshoor, S. Ebrahimi, and Y. Zhang, “Frequency analysis of a typical planar flexible multibody system with joint clearances,” Mechanism and Machine Theory, Vol. 126, pp. 429–456, Aug. 2018, https://doi.org/10.1016/j.mechmachtheory.2018.04.027
-
U. Starossek, “Forced response of low-frequency pendulum mechanism,” Mechanism and Machine Theory, Vol. 99, pp. 207–216, May 2016, https://doi.org/10.1016/j.mechmachtheory.2016.01.004
-
S. Wang, L. Hua, C. Yang, Y.O. Zhang, and X. Tan, “Nonlinear vibrations of a piecewise-linear quarter-car truck model by incremental harmonic balance method,” Nonlinear Dynamics, Vol. 92, No. 4, pp. 1719–1732, Jun. 2018, https://doi.org/10.1007/s11071-018-4157-6
-
P. Alevras, S. Theodossiades, and H. Rahnejat, “On the dynamics of a nonlinear energy harvester with multiple resonant zones,” Nonlinear Dynamics, Vol. 92, No. 3, pp. 1271–1286, May 2018, https://doi.org/10.1007/s11071-018-4124-2
-
A. Sinha, S. K. Bharti, A. K. Samantaray, G. Chakraborty, and R. Bhattacharyya, “Sommerfeld effect in an oscillator with a reciprocating mass,” Nonlinear Dynamics, Vol. 93, No. 3, pp. 1719–1739, Aug. 2018, https://doi.org/10.1007/s11071-018-4287-x
-
G. Habib, G. I. Cirillo, and G. Kerschen, “Isolated resonances and nonlinear damping,” Nonlinear Dynamics, Vol. 93, No. 3, pp. 979–994, Aug. 2018, https://doi.org/10.1007/s11071-018-4240-z
-
A. L. P. Livorati, I. L. Caldas, C. P. Dettmann, and E. D. Leonel, “Crises in a dissipative bouncing ball model,” Physics Letters A, Vol. 379, No. 43-44, pp. 2830–2838, Nov. 2015, https://doi.org/10.1016/j.physleta.2015.09.016
-
Ruihai Li, Ruiayng Qiu, Yinghua Zhou, and Chuandong Li, “Existence and stability of periodic orbits of bouncing bail system with limiter of cubic nonlinearity,” 2017 4th International Conference on Information, Cybernetics and Computational Social Systems (ICCSS), pp. 208–212, 2017.
-
Ruiayng Qiu, Ruihai Li, Yinghua Zhou, and Chuandong Li, “Finite-time stability of bouncing ball system with the limiter of cubic nonlinearity,” 2017 4th International Conference on Information, Cybernetics and Computational Social Systems (ICCSS), pp. 166–169, 2017.
-
V. Glazunov, New Mechanisms in Contemporary Robot Engineering. (in Russian), Moscow: Tehnosphere, 2018.
-
H. Shinno, H. Yoshioka, and H. Sawano, “A newly developed long range positioning table system with a sub-nanometer resolution,” CIRP Annals, Vol. 60, No. 1, pp. 403–406, 2011, https://doi.org/10.1016/j.cirp.2011.03.027
-
W. Kokuyama, T. Shimoda, and H. Nozato, “Primary accelerometer calibration with two-axis automatic positioning stage,” Measurement, Vol. 204, p. 112044, Nov. 2022, https://doi.org/10.1016/j.measurement.2022.112044
-
K. Cai, Y. Tian, F. Wang, D. Zhang, and B. Shirinzadeh, “Development of a piezo-driven 3-DOF stage with T-shape flexible hinge mechanism,” Robotics and Computer-Integrated Manufacturing, Vol. 37, pp. 125–138, Feb. 2016, https://doi.org/10.1016/j.rcim.2015.07.004
-
C. Lin, M. Jiang, and S. Zheng, “Establishment and verification of the analytical model for the critical parameters in the kinematics model of the precision positioning stage,” Sensors and Actuators A: Physical, Vol. 320, p. 112572, Apr. 2021, https://doi.org/10.1016/j.sna.2021.112572
-
V. Ragulskienė, Vibro-Shock Systems (Theory and Applications). (in Russian), Vilnius: Mintis, 1974.
-
R. Kurila and V. Ragulskienė, Two-Dimensional Vibro-Transmissions. (in Russian), Vilnius: Mokslas, 1986.
-
K. Ragulskis, R. Bansevicius, R. Barauskas, and G. Kulvietis, Vibromotors for Precision Microrobots. New York: Hemisphere, 1988.
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.

