Sloshing mitigation using vertical cylindrical baffle

1. Introduction

Sloshing is a term used to describe low frequency motions of a liquid's free surface in a container that is only partially filled. These vibrations have a significant impact on the dynamic model of the structures containing the liquid, and their connection with the sloshing liquid may cause instability. In several industrial applications, such as the sea transportation of liquid cargo, aeronautical vehicles, and earthquake-resistant structures, it is essential to detect and manage sloshing in order to ensure safe operations. The adverse impact of sloshing is most frequently observed in the storage and transportation of liquid cargo.

During the control of guided missile in the aerospace industry, sloshing was first encountered. In this scenario, it came to know that sloshing can effect structure and stability of the container. Numerous experimental and numerical investigations have been done in the past to try and control the influence of splashing in tanks. The first detailed study on sloshing was provided by NASA, after it many numerical and analytical methods are presented to investigate the impact of sloshing in the tanks. Many of these methods are cited by Ibrahim [1]. Various shapes of damping devices are used to damp the sloshing induced forces. These device's effect on liquid vibrations behaviour is studied in [2-7]. An analytical and numerical analysis of the impact of horizontal plates on free oscillations in vessels is reported in [4, 8, 9]. The dynamic behaviours of flexible containers using various methods is determined in [10-12]. Researchers have paid a lot of attention to the behaviours of isolated tanks in recent years. Some of these are cited in [13, 14]. Effect of flexible membranes on free oscillations in the liquid reservoirs is reported in [15] and [16]. For circular cylindrical containers containing inviscid liquid, numerous tests and analysis have been conducted in past decades. These tests and analysis are shown in [17-19].

Through the literature review, it came to know that the use of cylindrical baffles is not much popular. In this study, the effect of open-ended cylindrical vertical baffle on the free vibrations of the fluid in half filled cylindrical tank is analysed.

2. Physical description

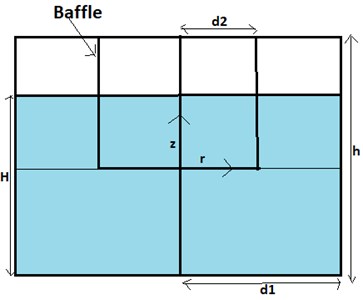
A rigid cylindrical container of radius $d_1$ and height $h$ which is half filled with an incompressible and non-viscous liquid is considered. A rigid open-ended cylindrical baffle of radius $d_2$ is inserted in the cylindrical container. It is half buried in the liquid. Cylindrical coordinates $(r,\theta ,z)$ is introduced in the fluid domain. Bottom of the container is represented by $z=-H$. The schematics diagram of the problem is shown in Fig. 1.

Fig. 1Cylindrical tank with vertical baffle

Using these premises, the below governing equation can be used to explain liquid flow inside the liquid domain in terms of velocity potential:

Since, the cylindrical container is rigid. Boundary condition is given by:

Free surface condition is given by:

3. Numerical results

ANSYS software is used to report the mode shapes of the baffle and fluid domain. In the present work, a rigid circular cylindrical container of radius $d_1=$ 1.5 m and height $h=$ 1.2 m which is filled with liquid up to $h=$ 0.8 m is considered. For numerical simulation, radius of rigid vertical open-ended cylindrical baffle is taken $d_2=$ 0 m, $d_2=$ 0.135 m, $d_2=$ 0.24 m, and $d_2=$ 0.32 m respectively.

Firstly, an unbaffled cylindrical container is considered. Table 1 demonstrated the frequencies corresponding to first six modes. It is clearly visible that the highest first frequency value is reported corresponding to first mode.

Mode shapes of the unbaffled cylindrical container of radius $d_1=$ 1.5 m are shown in Fig. 2. These pressure patterns display the splashing in cylindrical container.

Secondly, a rigid vertical cylindrical baffle is inserted inside the cylindrical container. Dimensions used for numerical simulation are $h=$ 1.2 m and $d_1=$ 1.5 m respectively. Baffle radius and height is considered $d_2=$ 0.24 m and $h=$ 0.7 m respectively. First six frequencies of baffled container are displayed in Table 2. It is noted that frequencies values are falling after inserting the cylindrical baffle inside the container. Mode shapes of the free liquid vibrations of baffled container are shown in the Fig. 3.

Fig. 2Mode shapes of free oscillations in un-baffled container

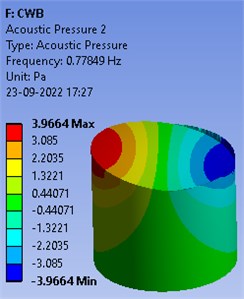
Fig. 3Mode shapes of free oscillations in baffled container

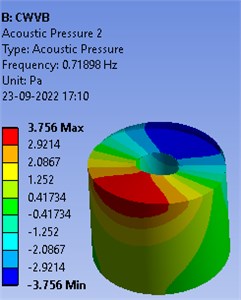
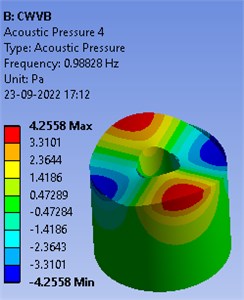
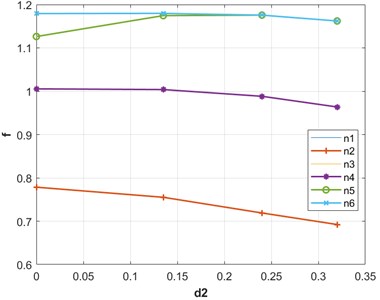
Table $3$ lists the frequencies of axisymmetric modes for different values of $d_2$. It is noticed that the frequency values decrease as the baffle’s radius increases. Lowest frequency value is noted corresponding to radius $d_2=$ 0.32 m.

Frequency dependence with respect to baffle’s radius $d_2$ is shown in Fig. 4. These curves are depicted for various baffle’s radius values $d_2=$ 0, $d_2=$ 0.135 m, $d_2=$ 0.24 m and $d_2=$ 0.32 m respectively. It also demonstrates the impact of baffle's radius. It is clear that frequency values decrease when the baffle’s radius is raised.

Fig. 4Frequencies versus baffle's radius

4. Conclusions

In this study, an impermeable and inviscid fluid that is partially contained in a rigid cylindrical container is examined. The impact of rigid open-ended cylindrical baffle positioned inside the container is examined. Mode shapes of the free vibrations of the liquid in the tank with and without baffle is demonstrated. Sloshing frequencies for various values of $d_2$ are reported. The results showed that frequency values are depending on the baffle's radius. It is noticed that frequency values falls as the baffle radius is increased.