The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock

Youssef, Hamdy M.; Salem, Raafat A. A.

doi:10.21595/jets.2022.22945

Journal of Engineering and Thermal Sciences

Browse Journal

Submit article

Published: 25 October 2022

Check for updates

The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock

Hamdy M. Youssef¹

Raafat A. A. Salem²

¹Mechanical Engineering Department-College of Engineering and Islamic Architecture, Umm Al, Qura University, Makkah, Saudi Arabia

²Mathematical Sciences Department, College of Applied Sciences, Umm Al, Qura University, Makkah, Saudi Arabia

Corresponding Author:

Hamdy M. Youssef

Cite the article Download PDF

Downloads 443

CrossRef Citations 4

Abstract

The current paper is dealing with the thermal reaction and response of skin tissue subjected to a constant heat flux due to thermo-electrical shock on the bounding plane. The dual-phase-lag bio heat conduction equation based on the Tzou model has been applied and solved in the Laplace transform domain by using a direct method. The numerical inversions of the Laplace transform, and numerical solution has been obtained. The thermos-electrical shock for a small value of time has been considered with constant voltage and resistance. The temperature increment responses have been obtained and discussed with various values of voltage, resistance, and dual-lag value times. Moreover, a comparison between the well-known three models of bioheat conduction of Pennes, Ventott-Cattaneo, and Tzou has been shown in the figure. The results show that the voltage, resistance, and dual-lag value of times have significant effects on the temperature increment distribution and the thermal wave propagation through the skin tissue.

The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock

Highlights

This research examined how skin tissue responds to a steady heat flux caused by a thermo-electrical shock on the bounding plane in terms of temperature reaction and response.
A direct technique has been used to apply and solve the dual-phase-lag bio heat conduction equation based on the Tzou model in the domain of the Laplace transform.
The voltage, resistance, and dual-lag time values significantly affect the distribution of temperature increments and the propagation of thermal waves through skin tissue.
The Tzou model is the most effective model that accurately predicts the physical behaviour of skin tissue.
The Tzou and Ventott-Cattaneo models also provide a thermal wave that propagates with a limited speed and is extremely similar to one another.

1. Introduction

Many treatments and their applications depend heavily on temperature transmission via live skin tissue. Microwaves, lasers, and other technological advancements have also expanded the field of bioheat transfer work [1]. Researcher Pennes, who improved the parabolic differential equation of the biological tissues for the first bioheat transfer, provides commentary on biothermal transmission analyses in real biological tissues [2]. Additionally, the consistency and nature of thermal activity in biological tissues have been modelled using the Pennes biological transmission approach. Similarities to such erratic outcomes that exhibit non-Fourier or hyperbolic conduction behaviour on the outside. To characterize the kind of hyperbolic equation, Cattaneo and Vernotte gave several modifications of heat conduction of Fourier's law in its linearity form [3, 4]. They proposed a thermal wave model to evaluate the impact of microwave and flux thermal activity. To treat diverse skin tissue disorders without harming the healthy tissue surrounding them, many sorts of treatments have been attempted. The Pennes bioheat transfer equation (PBTE) was analytically solved by Xu et al. They also studied the skin tissue bioheat transmission, skin thermal damage, tissue structure, skin biomechanics, and biothermomechanics [5] The dual-phase-lag (DPL), parabolic models of biomass transport, and hyperbolic were used to examine the non-Fourier thermomechanical activity of skin tissues in the context of various thermal loading limitations on the surface. Xu and colleagues also observed significant differences between Pennes, thermal waves, and dual-phase-lag (DPL) [6]. Additionally, Rossmann et al. analyzed how biological tissues’ perfusion, thermal characteristics, and dielectric properties change with the temperature at hyperthermic and ablation temperatures [7]. The dual-phase-lag (DPL) approach has been used to expand Tzou’s model while considering the relaxation activity at a high rate of reaction. Despite the slow procedure, the small-scale reaction is detected in time [8, 9]. Tzou introduced a new parameter time of phase lag for a temperature gradient [10]. Dual-phase-lag (DPL) heat conduction model has been used by Askarizadeh et al. to address transient heat transmission issues in skin tissue [11].

Before analyzing the general bioheat transfer paradigm in live tissue, Liu et al. [12]. The two-stage model for heat transmission issues in biological tissue uses the hyperthermia process to assess Liu et al. [13, 14]. The Liu and Chen thermal conductor model (DPL) employed non-Fourier thermal activity to characterize the thermal transit taking place in biological tissue and to diagnose hyperthermia [15].

Liu and Xu developed a closed-form analytical method to solve the Pennes bioheat equation for fluctuations in skin tissue temperature caused by sinusoidal heat flow [16]. Ahmadika et al. will have the analytical solution for the Pennes equations’ bioheat (parabolize) and hyperbolized bioheat transfer models for periodic constant and pulsed train heat flow boundary conditions [17]. Youssef and Alghamdi investigated a one-dimensional application of thermoelastic dual-phase-lag (DPL) in skin tissue under specific heat stress [18].

The body resists the flow of current. The skin is where the body experiences more than 99 % of its total electrical resistance. Ohms are used to measuring resistance. A calloused, dry hand may contain more than 100,000 due to the stratum corneum’s thick outer layer of dead cells. Due to the damp, moderately salty tissues beneath the skin, the internal body resistance is around 300. If there is skin breakdown due to high voltage, a cut, a severe abrasion, or submersion in water, the skin resistance can be efficiently overcome [19-21]. The skin behaves similarly to a capacitor or other electrical device in that it permits greater current to pass when voltage changes quickly. If one's hand is holding a metal instrument that abruptly comes into contact with a source of voltage, a quickly varying voltage will be applied to the palm and fingers. This kind of interaction will result in a substantially higher body current amplitude than would otherwise happen [19-21].

A quick, intense reaction to an electric current flowing through any portion of a person’s body is known as an electric shock. Electric shock results in electrocution, which is death. Tissue damage caused by electrical current, or voltage is referred to as primary electrical injury. Falls are a frequent source of secondary injuries. High resistance in the skin’s outer layer disintegrates above 500 V or greater. This significantly reduces the body’s resistance to current flow [19-21]. As a result, the quantity of current that flows at any given voltage increases. Skin breakdown can occasionally appear as tiny wounds the size of a pinhead that is simple to ignore. They frequently indicate that a significant quantity of current could enter the body. Muscles, nerves, and other tissues may sustain profound tissue damage because of this current. This is one of the reasons why high-voltage accidents frequently result in considerable deep tissue harm but little surface burns [19-21]. Youssef and El-Bary studied the thermal damage of the tumour tissue due to the thermoelectrical effect based on the Thomson effect. Different voltage and resistance effects have been studied and discussed in this work for three different types of tumour tissues [22].

The present paper’s goal is to build a mathematical model of bioheat skin tissue within the framework of a dual-phase-lag heat conduction model (Tzou model). The skin tissue’s surface is treated with an electrical shock with a constant voltage for a short period. The work is unique in that it investigates the impacts of dual-phase-lag time parameters, voltage value, and skin resistance on the temperature increment distribution using three distinct bioheat models: Pennes, Ventott-Cattaneo, and Tzou.

1.1. Pennes model of bioheat transfer for biological tissues

The bioheat transmission model was developed to examine the time-dependent temperature change as a heat response generated by either a heat source or thermal heating. Pennes developed the first model of biological tissues based on Fourier's law of heat conduction, which is as follows [18, 23, 24]:

1

K \nabla^{2} T = ρ C \frac{\partial T}{\partial t} - ρ_{b} w_{b} C_{b} (T_{b} - T) - (Q_{m e t} + Q_{e x t}),

where $ρ$ , $C$ and $K$ are the density, specific heat, and thermal conductivity of the tissue, respectively. $C_{b}$ , $w_{b}$ , $ρ_{b}$ and $T_{b}$ denote the specific heat of the blood, blood perfusion rate, blood density, and blood temperature, respectively. $T$ is the absolute temperature function. $Q_{m e t}$ denotes the metabolic heat generated by the chemical reaction inside the tissue, and it is constant, and the external heat source is given by $Q_{e x t}$ . Moreover, $\nabla^{2}$ is the Laplace operator.

1.2. The Ventott-Cattaneo model of bioheat conduction (Modified Fourier law)

Ventott-Cattaneo (V-C) amended the conventional Fourier thermal drive law by postulating the assumption of limited thermal wave propagation speed, resulting in the following hyperbolic form of the thermal wave [18, 23, 24]:

2

K \nabla^{2} T = ρ C (1 + τ_{q} \frac{\partial}{\partial t}) \frac{\partial T}{\partial t} + w_{b} C_{b} ρ_{b} (1 + τ_{q} \frac{\partial}{\partial t}) (T - T_{b})

- (1 + τ_{q} \frac{\partial}{\partial t}) (Q_{m e t} + Q_{e x t}),

where $τ_{q} = \frac{α}{c_{0}^{2}} > 0$ is a material property and is called the relaxation time parameter, and $α$ is the thermal diffusivity while $c_{0}$ is the speed of the thermal wave inside the medium.

1.3. Dual-phase-lag model (DPL) of bioheat transfer (Tzou model)

The dual-phase-lag (DPL) model based on the dual reaction between the gradient of the temperature $\nabla T$ and the heat flux $q$ has been modified by Tzou to be in the following heat conduction equation [18, 23, 24]:

3

K (1 + τ_{T} \frac{\partial}{\partial t}) \nabla^{2} T = ρ C (1 + τ_{q} \frac{\partial}{\partial t}) \frac{\partial T}{\partial t} + w_{b} C_{b} ρ_{b} (1 + τ_{q} \frac{\partial}{\partial t}) (T - T_{b})

- (1 + τ_{q} \frac{\partial}{\partial t}) (Q_{m e t} + Q_{e x t}),

where $τ_{T} \geq 0$ is the second parameter of the relaxation time, which is the phase lag of the temperature gradient passing through the medium.

We assume the temperature increment as follows:

4

θ = T - T_{b} .

Hence, we have:

5

K (1 + τ_{T} \frac{\partial}{\partial t}) \nabla^{2} θ = ρ C (1 + τ_{q} \frac{\partial}{\partial t}) \frac{\partial θ}{\partial t} + w_{b} C_{b} ρ_{b} (1 + τ_{q} \frac{\partial}{\partial t}) θ

- (1 + τ_{q} \frac{\partial}{\partial t}) (Q_{m e t} + Q_{e x t}) .

2. Basic formulation

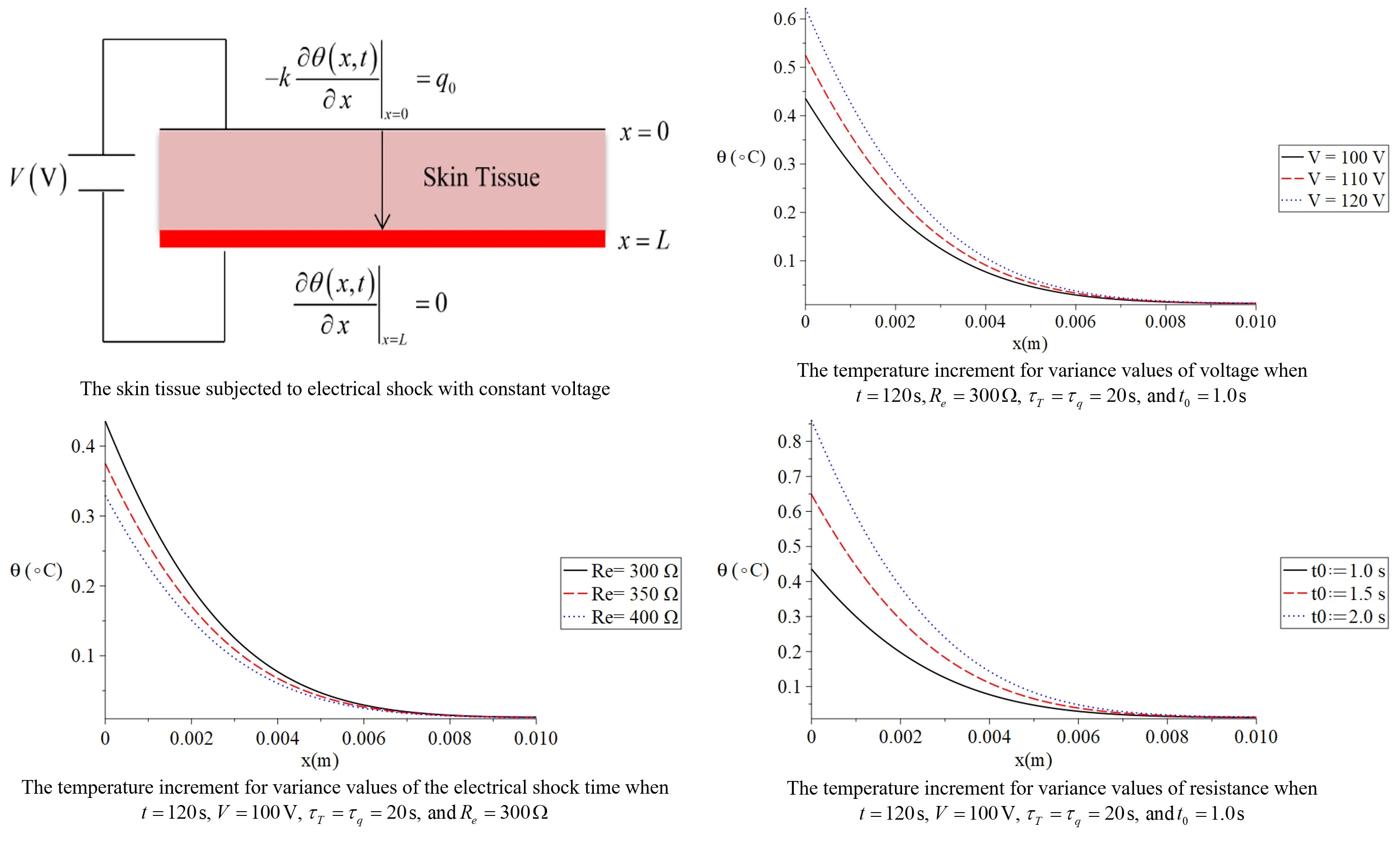
We proposed the medium $0 \leq x \leq L$ has been filled with skin tissue as in figure 1 and obeys the dual-phase-lag (DPL) as in Eq. (5) [18, 24].

Initially, the medium is dormant and has no external heat source $(Q_{e x t} = 0)$ while the metabolic heat source $Q_{m e t}$ is constant. The bounding plane of the outer surface of the skin tissue $x = 0$ is subjected to constant heat flux $q_{0}$ , while the bounding plane of the inner surface $x = L$ has no heat flux (see Fig. 1).

Hence, the heat conduction equations take the forms:

6

(τ_{T} \frac{\partial}{\partial t} + 1) \frac{\partial^{2} θ}{\partial x^{2}} = (\frac{τ_{q} ρ C}{K} \frac{\partial^{2}}{\partial t^{2}} + \frac{(ρ C + τ_{q} w_{b} C_{b} ρ_{b})}{K} \frac{\partial}{\partial t} + \frac{w_{b} C_{b} ρ_{b}}{K}) θ - \frac{Q_{m e t}}{K} .

Fig. 1The skin tissue subjected to electrical shock with constant voltage

The initial conditions are:

7

{θ (x, t)|}_{t = 0} = {\frac{\partial θ (x, t)}{\partial t}|}_{t = 0} = 0 .

The boundary conditions are:

8

{\frac{\partial θ (x, t)}{\partial x}|}_{x = 0} = - \frac{q_{0}}{K}, {\frac{\partial θ (x, t)}{\partial x}|}_{x = L} = 0 .

The solution in the Laplace transform domain:

9

\bar{F} (x, s) = L (f (x, t)) = \int_{0}^{\infty} f (x, t) e^{- s t} d t, t \geq 0,

where the inverse of the Laplace transform takes the form:

10

L^{- 1} (\bar{f} (s)) = f (t) \approx \frac{e^{κ t}}{t} [\frac{1}{2} \bar{f} (κ) + R e \sum_{n = 1}^{N} {(- 1)}^{n} \bar{f} (κ + \frac{i n π}{t})],

where $R e$ means the real part, while $i$ is the imaginary number unit, for faster convergence, many experiments confirmed that the value of the parameter $κ$ could satisfy the relation $κ t \approx$ 4.7 [8, 25].

Then, we have:

11

\frac{d^{2} \bar{θ} (x, s)}{d x^{2}} - λ^{2} (s) \bar{θ} (x, s) = - γ (s),

where:

12

λ^{2} (s) = \frac{τ_{q} ρ C s^{2} + (ρ C + τ_{q} w_{b} C_{b} ρ_{b}) s + w_{b} C_{b} ρ_{b}}{(τ_{T} s + 1) K}, γ (s) = \frac{Q_{m e t}}{s K},

{\frac{d \bar{θ} (x, s)}{d x}|}_{x = 0} = - \frac{q_{0}}{s K}, {\frac{d \bar{θ} (x, s)}{d x}|}_{x = L} = 0 .

The skin tissue is subjected to thermal shock that comes from the thermal effect due to electrical shock with constant voltage (Joule’s equation of electrical heating) $V (V)$ and constant resistance $R_{e} (Ω)$ when the current has a vibration of 60 Hz, the mean value of the skin resistance will be considered in the range 300-400 Ω [7, 19-22].

Then, Joule’s equation of electrical heating is given by [7, 19, 21, 22]:

13

q_{0} = \frac{V^{2} t_{0}}{R_{e}},

where $t_{0} (t_{0} > 0)$ is a parameter which gives the time interval of the electrical shock.

The general solution of the Eq. (11) is given by:

14

\bar{θ} (x, s) = θ_{1} (s) e^{- λ x} + θ_{2} (s) e^{λ x} + \frac{γ (s)}{λ^{2} (s)},

where $θ_{1} (s)$ and $θ_{2} (s)$ are some parameters which must be determined by using the boundary condition Eq. (12).

Hence, we have:

15

- θ_{1} + θ_{2} = - α, - θ_{1} e^{- λ L} + θ_{2} e^{λ L} = 0,

where $α = q_{0} / s K λ$ .

By solving the above system, we obtain:

16

θ_{1} = \frac{α e^{λ L}}{e^{λ L} - e^{- λ L}}, θ_{2} = \frac{α e^{- λ L}}{e^{λ L} - e^{- λ L}} .

Then, we have the solution in the form:

17

\bar{θ} (x, s) = \frac{α c o s h (λ (L - x))}{s i n h (L λ)} + \frac{γ}{λ^{2}},

which completes the solution in the Laplace transform domain where the solution in the physical time domain can be obtained by applying iteration Eq. (10).

3. Numerical results

The temperature distribution through skin tissue is explored in this work using three bioheat transfer models (Pennes, Ventott-Cattaneo, and Tzou) under constant heat flow circumstances on the skin surface. Table 1 shows the values of the essential thermal parameters employed in the current computations [5, 18, 23, 24, 26].

Table 1The material properties of the skin tissue

Parameter	Value	Unit	Parameter	Value	Unit
$K$	0.215	W/m°C	$W_{b}$	0.00052	ml/C m
$ρ$	1000	kg/m³	$T_{b}$	37	°C
$ρ_{b}$	1060	kg/m³	$τ_{T}, τ_{q}$	20.0	s
$C$	4187	J/kg°C	$t_{0}$	1.0	s
$C_{b}$	3800	J/kg°C	$L$	0.01	m

4. Discussions

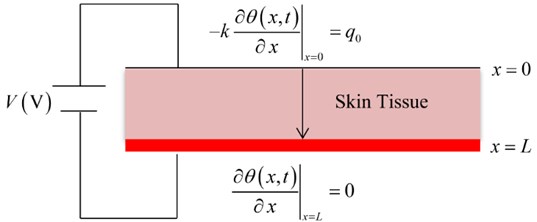
Fig. 2 shows the temperature increment distribution for variance values of voltage $V =$ (100, 110, 120) V when $t =$ 120 s, $R_{e} =$ 300 Ω, $τ_{T} = τ_{q} =$ 20 s, and $t_{0} =$ 1.0 s. It is noted that the value of the voltage of the thermo-electrical shock has a significant effect on the thermal wave. The value of the temperature increment increases when the value of the voltage increases. The values of the temperature increment on the boundary of the skin tissue $x = 0$ take the following order:

18

{θ (V = 100 V)|}_{x = 0} < {θ (V = 110 V)|}_{x = 0} < {θ (V = 120 V)|}_{x = 0} .

Fig. 3 shows the temperature increment distribution for variance values of skin tissue resistance $R_{e} =$ (300, 350, 400) Ω when $t =$ 120 s, $V =$ 100 V, $τ_{T} = τ_{q} =$ 20 s, and $t_{0} =$ 1.0 s. It is noted that the value of the voltage of the skin tissue resistance has a significant effect on the thermal wave. The value of the temperature increment decreases when the value of the skin tissue resistance increases. The values of the temperature increment on the boundary of the skin tissue $x = 0$ take the following order:

19

{θ (R_{e} = 400 Ω)|}_{x = 0} < {θ (R_{e} = 350 Ω)|}_{x = 0} < {θ (R_{e} = 300 Ω)|}_{x = 0} .

Fig. 2The temperature increment for variance values of voltage when t= 120 s, Re= 300 Ω, τT=τq= 20 s, and t0= 1.0 s.

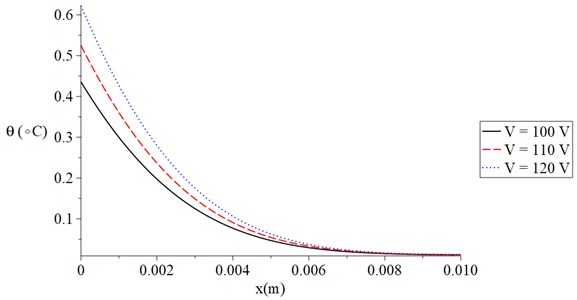
Fig. 3The temperature increment for variance values of resistance when t= 120 s, V= 100 V, τT=τq= 20 s, and t0= 1.0 s

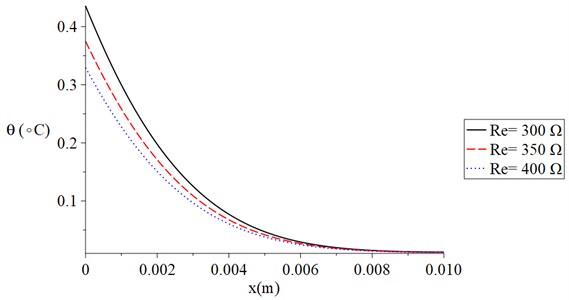
Fig. 4 shows the temperature increment distribution for variance values of electrical shock time $t_{0} =$ (1.0, 1.5, 2.0) s when $t =$ 120 s, $V =$ 100 V, $τ_{T} = τ_{q} =$ 20 s, and $R_{e} =$ 300 Ω. It is noted that the value of the electrical shock time has a significant effect on the thermal wave. The value of the temperature increment increases when the value of the electrical shock time increases. The values of the temperature increment on the boundary of the skin tissue $x = 0$ take the following order:

20

{θ (t_{0} = 1.0 s)|}_{x = 0} < {θ (t_{0} = 1.5 s)|}_{x = 0} < {θ (t_{0} = 2.0 s)|}_{x = 0} .

Fig. 5 shows the temperature increment distribution for variance situations of the dual-lag times parameters $(τ_{q} < τ_{T}, τ_{q} = τ_{T}, τ_{q} > τ_{T})$ when $t =$ 120 s, $V =$ 100 V, $t_{0} =$ 1.0 s and $R_{e} =$ 300 Ω. It is noted that the value of the dual-lag times parameters has a significant effect on the thermal wave. The values of the temperature increment on the boundary of the skin tissue $x = 0$ take the following order:

21

{θ (τ_{T} < τ_{q})|}_{x = 0} < {θ (τ_{T} = τ_{q})|}_{x = 0} < {θ (τ_{T} > τ_{q})|}_{x = 0} .

We can see that the situation when the value of the lag-time of the temperature is smaller than the value of the lag-time parameter of the temperature gradient, generates a thermal wave which has a finite speed of propagation where in this case, the temperature increment goes to zero before the other two cases.

Fig. 4The temperature increment for variance values of the electrical shock time when t= 120 s, V= 100 V, τT=τq= 20 s, and Re= 300 Ω

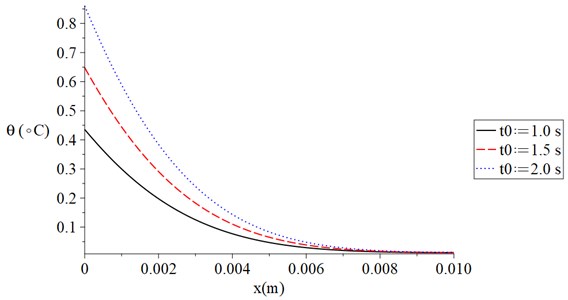
Fig. 5The temperature increment for variance situations of the dual-lag times parameters when t= 120 s, V= 100 V, t0= 1.0 s and Re= 300 Ω

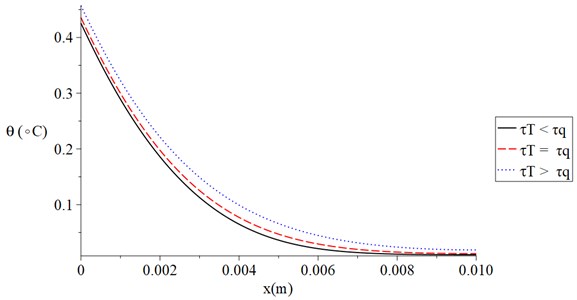
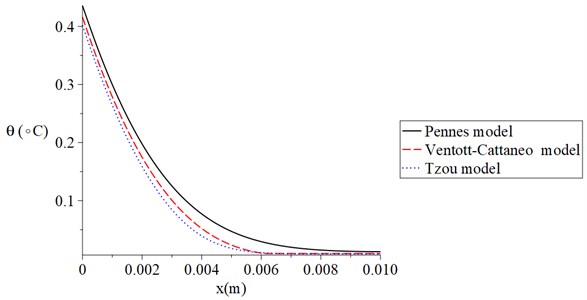
Fig. 6 shows the temperature increment distribution for Pennes, Ventott-Cattaneo, and Tzou models when $t =$ 120 s, $V =$ 100 V, $t_{0} =$ 1.0 s, and $R_{e} =$ 300 Ω. It is noted that the temperature increment distribution has different values based on the three different models. The values of the temperature increment take the following order:

22

θ (T z o u) < θ (V e n t o t t - C a t t a n e o) < θ (P e n n e s) .

The results of this figure proved that the Tzou model is the most successful model which agrees with the physical behaviour of the skin tissue. Moreover, Tzou and Ventott-Cattaneo models are very close and offer a thermal wave propagating with a finite speed.

Fig. 6The temperature increment for Pennes, Ventott-Cattaneo, and Tzou models when t= 120 s, V= 100 V, t0= 1.0 s, and Re= 300 Ω

5. Conclusions

This research examined how skin tissue responds to a steady heat flux caused by a thermo-electrical shock on the bounding plane in terms of temperature reaction and response. A direct technique has been used to apply and solve the dual-phase-lag bio heat conduction equation based on the Tzou model in the domain of the Laplace transform. The Laplace transforms’ numerical inversions and solutions have been discovered. With constant voltage and resistance, the thermos-electrical shock for a short period has been explored.

With different voltage, resistance, and dual-lag time values, the temperature increment responses have been measured and discussed. Additionally, a comparison of the well-known Pennes, Ventott-Cattaneo, and Tzou bioheat conduction models has been illustrated.

The findings demonstrate that the voltage, resistance, and dual-lag time values significantly affect the distribution of temperature increments and the propagation of thermal waves through skin tissue.

The outcomes of this research demonstrated that the Tzou model is the most effective model that accurately predicts the physical behaviour of skin tissue. The Tzou and Ventott-Cattaneo models also provide a thermal wave that propagates with a limited speed and is extremely similar to one another.

References

F. Xu, T. J. Lu, K. A. Seffen, and E. Y. K. Ng, “Mathematical modeling of skin bioheat transfer,” Applied Mechanics Reviews, Vol. 62, No. 5, p. 05080, Sep. 2009, https://doi.org/10.1115/1.3124646

Publisher
H. H. Pennes, “Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm,” Journal of Applied Physiology, Vol. 1, No. 2, pp. 93–122, Aug. 1948, https://doi.org/10.1152/jappl.1948.1.2.93

Publisher
C. Cattaneo, “A form of heat-conduction equations which eliminates the paradox of instantaneous propagation,” Comptes Rendus, Vol. 247, p. 431, 1958.

Search CrossRef
P. Vernotte, “Les paradoxes de la theorie continue de l’equation de la chaleur,” in Comptes Rendus, Vol. 246, p. 3154, 1958.

Search CrossRef
F. Xu, T. J. Lu, and K. A. Seffen, “Biothermomechanical behavior of skin tissue,” Acta Mechanica Sinica, Vol. 24, No. 1, pp. 1–23, Feb. 2008, https://doi.org/10.1007/s10409-007-0128-8

Publisher
F. Xu, K. A. Seffen, and T. J. Lu, “Non-Fourier analysis of skin biothermomechanics,” International Journal of Heat and Mass Transfer, Vol. 51, No. 9-10, pp. 2237–2259, May 2008, https://doi.org/10.1016/j.ijheatmasstransfer.2007.10.024

Publisher
C. Rossmanna and D. Haemmerich, “Review of temperature dependence of thermal properties, dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures,” Critical Reviews in Biomedical Engineering, Vol. 42, No. 6, pp. 467–492, 2014, https://doi.org/10.1615/critrevbiomedeng.2015012486

Publisher
D. Y. Tzou, “A unified field approach for heat conduction from macro – to micro-scales,” Journal of Heat Transfer, Vol. 117, No. 1, pp. 8–16, Feb. 1995, https://doi.org/10.1115/1.2822329

Publisher
D. Jou, “DY Tzou: macro-to microscale heat transfer. the lagging behaviour. series in chemical and mechanical engineering,” Journal of Non Equilibrium Thermodynamics, Vol. 23, No. 2, pp. 192–193, 1998.

Search CrossRef
M. N. O. ¨Zis¸Ik and D. Y. Tzou, “On the wave theory in heat conduction,” Journal of Heat Transfer, Vol. 116, No. 3, pp. 526–535, Aug. 1994, https://doi.org/10.1115/1.2910903

Publisher
H. Askarizadeh and H. Ahmadikia, “Analytical analysis of the dual-phase-lag model of bioheat transfer equation during transient heating of skin tissue,” Heat and Mass Transfer, Vol. 50, No. 12, pp. 1673–1684, Dec. 2014, https://doi.org/10.1007/s00231-014-1373-6

Publisher
K.-C. Liu, Y.-N. Wang, and Y.-S. Chen, “Investigation on the bio-heat transfer with the dual-phase-lag effect,” International Journal of Thermal Sciences, Vol. 58, pp. 29–35, Aug. 2012, https://doi.org/10.1016/j.ijthermalsci.2012.02.026

Publisher
K.-C. Liu and H.-T. Chen, “Analysis for the dual-phase-lag bio-heat transfer during magnetic hyperthermia treatment,” International Journal of Heat and Mass Transfer, Vol. 52, No. 5-6, pp. 1185–1192, Feb. 2009, https://doi.org/10.1016/j.ijheatmasstransfer.2008.08.025

Publisher
K.-C. Liu, H.-T. Chen, and P.-J. Cheng, “Inverse investigation of non-Fourier heat conduction in tissue,” Journal of Thermal Biology, Vol. 62, pp. 123–128, Dec. 2016, https://doi.org/10.1016/j.jtherbio.2016.07.002

Publisher
K.-C. Liu and H.-T. Chen, “Investigation for the dual phase lag behavior of bio-heat transfer,” International Journal of Thermal Sciences, Vol. 49, No. 7, pp. 1138–1146, Jul. 2010, https://doi.org/10.1016/j.ijthermalsci.2010.02.007

Publisher
Jing Liu and L. X. Xu, “Estimation of blood perfusion using phase shift in temperature response to sinusoidal heating at the skin surface,” IEEE Transactions on Biomedical Engineering, Vol. 46, No. 9, pp. 1037–1043, 1999, https://doi.org/10.1109/10.784134

Publisher
H. Ahmadikia, R. Fazlali, and A. Moradi, “Analytical solution of the parabolic and hyperbolic heat transfer equations with constant and transient heat flux conditions on skin tissue,” International Communications in Heat and Mass Transfer, Vol. 39, No. 1, pp. 121–130, Jan. 2012, https://doi.org/10.1016/j.icheatmasstransfer.2011.09.016

Publisher
H. M. Youssef and N. A. Alghamdi, “Modeling of one-dimensional thermoelastic dual-phase-lag skin tissue subjected to different types of thermal loading,” Scientific Reports, Vol. 10, No. 1, pp. 1–12, Dec. 2020, https://doi.org/10.1038/s41598-020-60342-6

Publisher
R. M. Fish and L. A. Geddes, “Conduction of electrical current to and through the human body: a review,” Eplasty, Vol. 9, 2009.

Search CrossRef
R. M. Fish and L. A. Geddes, “Electrophysiology of connection current spikes,” Cardiovascular Engineering, Vol. 8, No. 4, pp. 219–224, Dec. 2008, https://doi.org/10.1007/s10558-008-9059-7

Publisher
S. Grimnes, “Dielectric breakdown of human skinin vivo,” Medical and Biological Engineering and Computing, Vol. 21, No. 3, pp. 379–381, May 1983, https://doi.org/10.1007/bf02478510

Publisher
H. M. Youssef and A. A. El-Bary, “Voltage and time required for irreversible thermal damage of tumor tissues during electrochemotherapy under thomson effect,” Mathematics, Vol. 8, No. 9, p. 1488, Sep. 2020, https://doi.org/10.3390/math8091488

Publisher
H. M. Youssef and N. A. Alghamdi, “Characterization of thermal damage due to two-temperature high-order thermal lagging in a three-dimensional biological tissue subjected to a rectangular laser pulse,” Polymers, Vol. 12, No. 4, p. 922, Apr. 2020, https://doi.org/10.3390/polym12040922

Publisher
H. M. Youssef and N. A. Alghamdi, “Three-dimensional biological tissue under high-order effect of two-temperature thermal lagging to thermal responses due to a laser irradiation,” 36th International Conference on Vibroengineering in Dubai, United Arab Emirates, March 15-17th, 2019, Vol. 22, pp. 112–117, Mar. 2019, https://doi.org/10.21595/vp.2019.20521

Publisher
D. Tzou and M.-T. M. H. Transfer, The Lagging Behavior. Washington: Taylor Francis, 1997.

Search CrossRef
Y. Zhang, “Generalized dual-phase lag bioheat equations based on nonequilibrium heat transfer in living biological tissues,” International Journal of Heat and Mass Transfer, Vol. 52, No. 21-22, pp. 4829–4834, Oct. 2009, https://doi.org/10.1016/j.ijheatmasstransfer.2009.06.007

Publisher

Cited by

The heat transfer in skin tissues under the general two-temperature three-phase-lag model of heat conduction with a comparative study

Eman A.N. Al-Lehaibi | Hamdy M. Youssef

(2024)

Thermo-Electrical Influence of Graphene Nano-Strip on Viscothermoelastic Nanobeam Vibration

Mohammad Salem J. Alzahrani | Najat A. Alghamdi | Hajar A. Alshehri

(2023)

Influence of the static pre-stress on the thermal quality factor of a micro-resonator under the dual-phase-lag heat conduction model

Eman A. N. Al-Lehaibi

(2023)

Influence of graphene nano-strips on the vibration of thermoelastic nanobeams

Mohammad Salem J. Alzahrani | Najat A. Alghamdi | Jamiel A. Alotaibi

(2023)

About this article

Received

21 September 2022

Accepted

20 October 2022

Published

25 October 2022

DOI

https://doi.org/10.21595/jets.2022.22945

Keywords

phase-lag

skin tissue

heat flux

Fourier series

thermo-electrical effect

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2023 06 26

Influence of the fractional-order strain on an infinite material with a spherical cavity under Green-Naghdi hyperbolic two-temperature thermoelasticity theory

Hamdy M. Youssef, Abdulrahman A. Alghamdi

Research article

2022 06 30

The vibration of a thermoelastic nanobeam due to thermo-electrical effect of graphene nano-strip under Green-Naghdi type-II model

Hamdy M. Youssef, Abdullah A. Al Thobaiti

Research article

2021 11 11

Influence of laser pulse on plane waves propagating in a thermoelastic medium with micro-temperature under the DPL model

Adnan Jahangir, Adiya Dar, Mohamed I. A. Othman

Research article

2021 10 12

Heat transfer and the influence of electromagnetic field and thermal time during temperature distribution in human tissue

Khaled Lotfy, Alla El-Bary

H. M. Youssef and R. A. A. Salem, “The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock,” Journal of Engineering and Thermal Sciences, Vol. 2, No. 2, pp. 114–123, Oct. 2022, https://doi.org/10.21595/jets.2022.22945

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jets.2022.22945
UR  - https://doi.org/10.21595/jets.2022.22945
TI  - The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock
T2  - Journal of Engineering and Thermal Sciences
AU  - Youssef, Hamdy M.
AU  - Salem, Raafat A. A.
PY  - 2022
DA  - 2022/10/25
PB  - JVE International Ltd.
SP  - 114-123
VL  - 2
IS  - 2
SN  - 2669-2465
ER  - 

Copy Ris

Copied to clipboard!

@article{Youssef_2022,
	doi = {10.21595/jets.2022.22945},
	url = {https://doi.org/10.21595/jets.2022.22945},
	year = 2022,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {2},
	number = {2},
	pages = {114--123},
	author = {Hamdy M. Youssef and Raafat A. A. Salem},
	title = {The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock},
	journal = {Journal of Engineering and Thermal Sciences}
}

Copy Bibtex

Copied to clipboard!

[1]H. M. Youssef and R. A. A. Salem, “The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock,” Journal of Engineering and Thermal Sciences, vol. 2, no. 2, pp. 114–123, Oct. 2022, doi: 10.21595/jets.2022.22945.

Copy IEEE

Copied to clipboard!

Youssef, Hamdy M., and Raafat A. A. Salem. “The Dual-Phase-Lag Bioheat Transfer of a Skin Tissue Subjected to Thermo-Electrical Shock.” Journal of Engineering and Thermal Sciences 2, no. 2 (October 25, 2022): 114–23. https://doi.org/10.21595/jets.2022.22945.

Copy Chicago

Copied to clipboard!

The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock

Abstract

Highlights

1. Introduction

1.1. Pennes model of bioheat transfer for biological tissues

1.2. The Ventott-Cattaneo model of bioheat conduction (Modified Fourier law)

1.3. Dual-phase-lag model (DPL) of bioheat transfer (Tzou model)

2. Basic formulation

3. Numerical results

4. Discussions

5. Conclusions

References

Cited by

About this article

Related Articles