Abstract
During functioning time, structures such as beams are subjected to a variety of loads caused by the working conditions and environment, which can lead to the development of cracks. The current research is concerned with detecting the presence and location of two transverse breathing cracks, in cantilever beams. Starting from the known fact that damages produce a stiffness degradation in structures altering their dynamic parameters, we performed modal simulations of damaged beams to determine their natural frequencies. By using the simulation data, we trained an artificial neural network (ANN), using the feedforward backpropagation algorithm, that is capable to detect the presence of the cracks, their position and for the case when the damages are in proximity, the model can determine if the cracks occur on the same face or opposite faces.
Highlights
- Determining the position and surface of transverse cracks in steel beam
- Machine learning models can be easily applied in detection of multiple cracks
- The superposition principle is valid until the crack effects interfere
1. Introduction
An important concern in today’s society is maintaining the safe operation of engineering structures, by detecting the occurrence of damages in an incipient state, thus avoiding the probability of catastrophes [1]-[4]. Fatigue cracks represent a great threat to the decommissioning of structures, which can be described as multiple cracks in the incipient state that can easily lead to structural failure [5]. The resonant frequencies of structures have proven to be a reliable damage indicator that can be applied to a variety of engineering structures [6], [7]. Extensive research has been made concerning the detection of one crack present in beams by using its modal parameters [8], [9], but few studies are concerned with the detection and localization of multiple cracks in structures. In paper [10] the authors determine the location and size of multiple non-propagating open cracks on beams with circular cross-sections by employing the flexibility matrices and modal parameters, but the method relies on both the natural frequencies and the mode shapes for a more precise determination. In paper [11] the effect of two cracks on a cantilever beam is demonstrated by the authors through FEM simulations, but the problem of processing the large database of damage signatures is not taken into consideration. Intelligent artificial neural networks have proven to be reliable for predicting the characteristics of multiple cracks [12]. Another important concern is finding the surface on which the crack is located. If more than one crack is present in a structure, the dynamic response becomes more complex, depending on their relative position, and the problem of detecting and locating the cracks becomes more difficult [13], [14]. We demonstrate in the current paper that novel intelligent methods can be applied successfully for evaluating two cracks that are present in a cantilever. We perform modal simulations, using the Ansys software, on damaged steel cantilever beams, affected by two breathing transverse cracks, that can be present on the same face or on opposite faces. After the natural frequency values are depicted for the proposed damage scenarios, we use the data for training an ANN model, using the MatLab software, that can determine the location of the two cracks and when the cracks are at a distance smaller than 5 mm relative to each other, the intelligent model can also determine if the damages are on the same face or on opposite faces. This phenomenon of strain energy interference when the cracks are close to each other is explained in more detail in the paper [14].
2. FEM simulations
The current study takes into consideration the occurrence of two cracks in a cantilever beam on the same face or on opposite faces. In recent research, [15], [16], direct and indirect methods based on the natural frequency are proposed for the identification of multiple cracks in beams. Direct methods include the simplified definition of natural frequency drops caused by cracks. The ratios of the natural frequencies obtained from the damaged and undamaged beams are determined by an approach that uses the local crack flexibility model. It was demonstrated in paper [15] that if the two cracks are in relative proximity, the modal response of the beam does not respect the superposition principle, acting similar to a beam affected by a branched crack.
Modal analyzes were performed in Ansys to extract the natural frequency values for a steel beam of a constant section, with the dimensions and physical-mechanical properties shown in Table 1.
Table 1Dimensions and physical-mechanical properties of the analyzed structure
Mechanical characteristics of the material | Beam’s main dimensions | |||||||
Density [kg/m3] | Young modulus [N/m2] | Poisson coefficient [–] | Tensile strength [MPa] | Yield strength [MPa] | Elong. [%] | [mm] | [mm] | [mm] |
7850 | 2·1011 | 0.3 | 470-630 | 355 | 20 | 1000 | 50 | 5 |
The cantilever and crack geometries are generated in the Ansys design modeler. The damages are defined as open transverse cracks, with a width of a maximum 0,04 mm, depth of 1 mm, and the position was specified as the distance from the left end of the bar to the crack, as shown in Fig. 1, for the case when the damages are on the same face.
Fig. 1Damaged cantilever beam, with cracks on the same surface
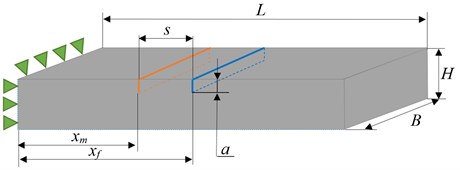
For the current study, we have defined damage scenarios with one crack positioned at 160 mm, and the second is iteratively replaced with a step of 0,5 mm to the left and to the right, in the interval 150…170 mm. Simulations were performed also by considering the second crack on the opposite face. For this means the Ansys modal simulation module was used, by applying a mesh of 2 mm maximum edge size of hexahedral elements. The boundary condition was set as fixed on the left face of the cantilever. The results depicted are the first five weak axis bending vibration modes, and the simulation configuration is shown in Fig. 2, for the cases with opposite transverse cracks.
After the simulations run, the results consisting of the natural frequencies for the first five transverse vibration modes are recorded and the results are plotted, relative to the undamaged beam’s natural frequencies, for the cases when the cracks are on the same face and on opposite faces in Fig. 3.
Fig. 2Damaged cantilever beam, with cracks on opposite faces

Fig. 3Natural frequency results obtained from FEM simulations
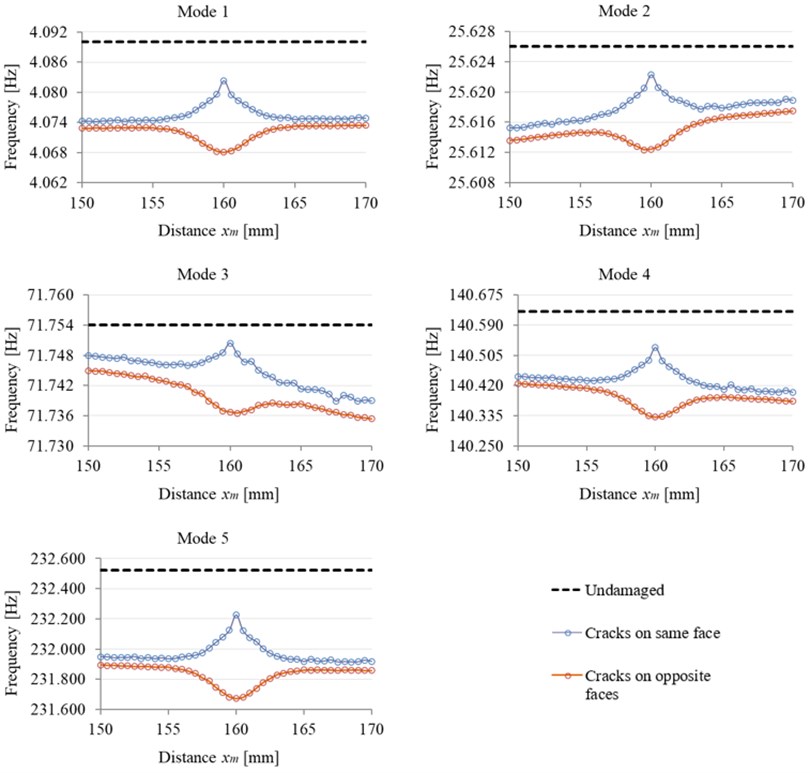
By analyzing how the superposition works, from the representations in Fig. 3 one can observe that in a narrow area where the state of tension due to the two cracks interferes, the effective effect on the beam frequency is smaller for the case when the cracks are on the same face, and for the cases with cracks on the opposite faces, the frequency drop is higher [14]-[16]. Because of this phenomenon, for the cases when the cracks are close to each other, by analyzing the damage signature, it is easy to specify if the cracks are on the same faces or on opposite sides. This conclusion leads to the possibility of developing an artificial neural network that can determine the presence, location, and if the cracks are close to each other, the side on which the damage occurs.
3. Development of the artificial neural network (ANN)
ANN’s are effective methods that can be applied in the field of Structural Health Monitoring, mainly by using the modal parameters of structures. Papers such as [17]-[19] describe the successful use of intelligent algorithms for the detection and quantification of cracks present in beams or plate like structures.
In the current research an artificial neural network is trained to evaluate the parameters of two transverse open cracks, present in a steel cantilever beam by determining the surface where the cracks are located, if they are in proximity, and if not, the ANN will still return the two cracks position relative to the fixed end. To this aim we used as training data, the first five natural frequencies determined through FEM simulations, as described in the previous chapter, resulting in five inputs. For the target data we have defined three outputs. The first output describes the surface on which the cracks occur, by considering three possible outputs for the crack location as: 0 in case the side on which the crack occurs is not possible to determine, 1 when the cracks occur on the same face and -1 when the cracks are on opposite faces. The second and third outputs describe the location of the two cracks and , relative to the fixed end in mm. The damage scenarios considered for the training faze is identical to the one presented in the previous chapter, meaning that the crack parameters remain 1 mm and positions 160 mm, 150-170 mm, but the training is done for a smaller dataset by considering the crack replacement step 1 mm.
We used the MatLab software for training a feedforward backpropagation neural network using the Bayesian Regularization function with the metadata presented in Table 2. The number of neurons is determined by applying the method shown in [20].
Table 2ANN metadata
Type of the network | Feed forward backpropagation |
Total number of hidden layers | 2 |
No. of neuron in the input layer | 5 |
No. of neuron in the hidden layers | 20 |
No. of neuron in the output layer | 3 |
Activation function | Hyperbolic tangent |
Performance validation | Mean square error |
Training algorithm | Bayesian regularisation |
The architecture of the ANN is also presented in Fig. 4.
After the training faze, the evaluation of the ANN’s performance is determined with the help of the Neural Network interface by plotting the performance and regression curves, as shown in Fig. 5.
Fig. 4ANN architecture

From the plotted regression and performance curves, the precision of ANN model is satisfying the accuracy needed for the evaluation of a beam with the damage scenarios described earlier. To prove its performance, we furthermore test the ANN by using the modal data generated for intermediate crack locations. The results obtained are shown in Table 3.
Fig. 5Network performance
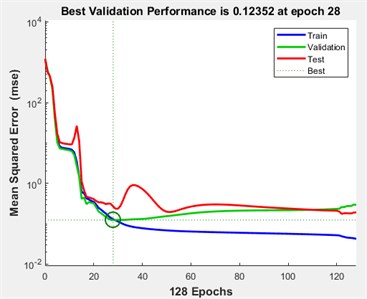
a) Best validation performance
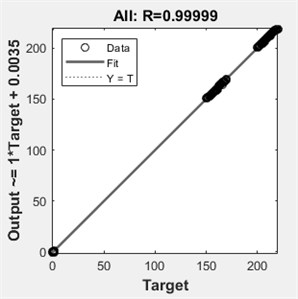
b) Error obtained for training, validating and testing
Table 3Results obtained using the developed ANN model
FEM parameters for the cracks | Results obtained using the ANN | ||||
Crack location [–] | Crack position [mm] | Crack position [mm] | Crack location [–] | Crack position [mm] | Crack position [mm] |
0 | 160 | 151.5 | 0 | 160 | 151.5144 |
0 | 160 | 152.5 | 0 | 160 | 152.073 |
0 | 160 | 153.5 | 0 | 160 | 153.2975 |
0 | 160 | 154.5 | 0 | 160 | 154.3013 |
1 | 160 | 156.5 | 1 | 160 | 156.7023 |
1 | 160 | 157.5 | 1 | 160 | 157.4772 |
1 | 160 | 158.5 | 1 | 160 | 158.6479 |
1 | 160 | 159.5 | 1 | 160 | 159.4589 |
1 | 160 | 160.5 | 1 | 160 | 159.8442 |
1 | 160 | 161.5 | 1 | 160 | 161.3919 |
1 | 160 | 162.5 | 1 | 160 | 162.7022 |
1 | 160 | 163.5 | 1 | 160 | 163.4433 |
0 | 160 | 165.5 | 0 | 160 | 165.0356 |
0 | 160 | 166.5 | 0 | 160 | 166.4032 |
0 | 160 | 167.5 | 0 | 160 | 167.5405 |
0 | 160 | 168.5 | 0 | 160 | 168.1396 |
0 | 160 | 169.5 | 0 | 160 | 169.0868 |
0 | 160 | 150.5 | 0 | 160 | 150.7552 |
0 | 160 | 151.5 | 0 | 160 | 151.4201 |
0 | 160 | 152.5 | 0 | 160 | 152.2887 |
0 | 160 | 153.5 | 0 | 160 | 153.3261 |
0 | 160 | 154.5 | 0 | 160 | 154.4424 |
–1 | 160 | 155.5 | 0 | 160 | 155.5578 |
–1 | 160 | 156.5 | –1 | 160 | 156.624 |
–1 | 160 | 157.5 | –1 | 160 | 157.5835 |
–1 | 160 | 158.5 | –1 | 160 | 158.5078 |
–1 | 160 | 159.5 | –1 | 160 | 159.3462 |
–1 | 160 | 160.5 | –1 | 160 | 160.5052 |
–1 | 160 | 161.5 | –1 | 160 | 161.642 |
–1 | 160 | 162.5 | –1 | 160 | 162.3833 |
–1 | 160 | 163.5 | –1 | 160 | 163.3912 |
–1 | 160 | 164.5 | –1 | 160 | 164.4716 |
0 | 160 | 165.5 | 0 | 160 | 165.4273 |
0 | 160 | 166.5 | 0 | 160 | 166.3988 |
0 | 160 | 167.5 | 0 | 160 | 167.4921 |
4. Conclusions
In the current research, we described the dynamic behavior of a cantilever steel beam, by using numerical methods, for different scenarios considering two open transverse cracks. By knowing that the frequency changes of the beam with multiple cracks had an effect similar to the sum of the frequency changes produced by each individual crack as long as the stress state of the damages does not interfere, it was possible to generate an ANN that can determine the position of the two cracks, and also the surface on which they occur when the damages interfere.
References
-
T. Y. Kam and T. Y. Lee, “Detection of cracks in structures using modal test data,” Engineering Fracture Mechanics, Vol. 42, No. 2, pp. 381–387, May 1992, https://doi.org/10.1016/0013-7944(92)90227-6
-
M. Awadallah and A. El-Sinawi, “Effect and detection of cracks on small wind turbine blade vibration using special Kriging analysis of spectral shifts,” Measurement, Vol. 151, p. 107076, Feb. 2020, https://doi.org/10.1016/j.measurement.2019.107076
-
A. S. Sekhar, “Crack detection and monitoring in a rotor supported on fluid film bearings: start-up versus run-down,” Journal of Mechanical Systems and Signal Processing, Vol. 17, No. 4, pp. 897–901, 2003.
-
W. C. Hurty, “Using substructures,” American Institute of Aeronautics and Astronautics Journal, Vol. 3, pp. 678–685, 1965.
-
U. Andreaus and P. Baragatti, “Fatigue crack growth, free vibrations, and breathing crack detection of aluminium alloy and steel beams,” The Journal of Strain Analysis for Engineering Design, Vol. 44, No. 7, pp. 595–608, Oct. 2009, https://doi.org/10.1243/03093247jsa527
-
W. M. Ostachowicz and M. Krawczuk, “Analysis of the effect of cracks on the natural frequencies of a cantilever beam,” Journal of Sound and Vibration, Vol. 150, No. 2, pp. 191–201, Oct. 1991, https://doi.org/10.1016/0022-460x(91)90615-q
-
J. Hu and R. Y. Liang, “An integrated approach to detection of cracks using vibration characteristics,” Journal of the Franklin Institute, Vol. 330, No. 5, pp. 841–853, Sep. 1993, https://doi.org/10.1016/0016-0032(93)90080-e
-
W. M. Ostachowicz and M. Krawczuk, “Analysis of effect of cracks on the mutual frequencies of a cantilever beam,” Journal of Sound and Vibration, Vol. 150, pp. 191–201, 1991.
-
Zhichun Yang and Le Wang, “Structural Damage Detection by Changes in Natural Frequencies,” in Journal of Intelligent Material Systems and Structures, Vol. 21, No. 3, pp. 309–319, Feb. 2010, https://doi.org/10.1177/1045389x09350332
-
M. Kisa and M. Arif Gurel, “Modal analysis of multi-cracked beams with circular cross section,” Engineering Fracture Mechanics, Vol. 73, No. 8, pp. 963–977, May 2006, https://doi.org/10.1016/j.engfracmech.2006.01.002
-
M. P. Kolhe, V. D. Wakchaure, and A. V. Deokar, “Vibration analysis of cantilever beam with multiple cracks using natural frequency as basic criterion,” International Journal of Advance Research and Innovative Ideas in Education, Vol. 1, No. 3, 2015.
-
M. Maurya, R. Mishra, and I. Panigrahi, “Multi crack detection in structures using artificial neural network,” in IOP Conference Series: Materials Science and Engineering, Vol. 402, p. 012142, Sep. 2018, https://doi.org/10.1088/1757-899x/402/1/012142
-
M. Behzad, A. Ghadami, A. Maghsoodi, and J. Michael Hale, “Vibration based algorithm for crack detection in cantilever beam containing two different types of cracks,” Journal of Sound and Vibration, Vol. 332, No. 24, pp. 6312–6320, Nov. 2013, https://doi.org/10.1016/j.jsv.2013.07.003
-
G.-R. Gillich et al., “Damage detection on a beam with multiple cracks: a simplified method based on relative frequency shifts,” Sensors, Vol. 21, No. 15, p. 5215, Jul. 2021, https://doi.org/10.3390/s21155215
-
D. Nedelcu, G.-R. Gillich, A. T. Aman, C. O. Hamat, and T. Manescu, “Assessing multiple cracks in beams by a method based on the damage location coefficients,” Vibroengineering Procedia, Vol. 23, pp. 49–54, Apr. 2019, https://doi.org/10.21595/vp.2019.20661
-
G.-R. Gillich, A. T. Aman, M. Abdel Wahab, and C. Tufisi, “Detection of multiple cracks using an energy method applied to the concept of equivalent healthy beam,” in Lecture Notes in Mechanical Engineering, pp. 63–78, 2020, https://doi.org/10.1007/978-981-13-8331-1_5
-
M. Seguini, N. Djamel, B. Djilali, S. Khatir, and M. Abdel Wahab, “Crack prediction in beam-like structure using ANN based on frequency analysis,” Frattura ed Integrità Strutturale, Vol. 16, No. 59, pp. 18–34, Dec. 2021, https://doi.org/10.3221/igf-esis.59.02
-
S. Khatir, D. Boutchicha, C. Le Thanh, H. Tran-Ngoc, T. N. Nguyen, and M. Abdel-Wahab, “Improved ANN technique combined with Jaya algorithm for crack identification in plates using XIGA and experimental analysis,” Theoretical and Applied Fracture Mechanics, Vol. 107, p. 102554, Jun. 2020, https://doi.org/10.1016/j.tafmec.2020.102554
-
N. Gillich et al., “Beam damage assessment using natural frequency shift and machine learning,” Sensors, Vol. 22, No. 3, p. 1118, Feb. 2022, https://doi.org/10.3390/s22031118
-
A. Minda, D. G. Burtea, G. R. Gillich, C. Tufisi, N. Gillich, and Z. I. Praisach, “Accurate frequency estimation using DFT and artificial neural networks,” in Eusipco, pp. 1551–1555, 2022.
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
