Sensitivity analysis of numerical model parameters for optimized PEH responses

2.1. Modal response

In order to experimentally assess the modal responses of the optimized PEHs shapes in terms of the oscillations of their free ends, and thus the first eigenfrequency of the studied devices, a suitable experimental setup is devised and realized. The setup, displayed in Fig. 3, consists of the studied optimized PEH (1), a clamping mechanism produced using additive manufacturing (AM) technologies and used to obtain the fixture of the PEH clamped end (2), as well as the Metrolaser 500V^® laser-Doppler vibrometer (3) with its respective control and DAQ interface (4) [18], all connected to a PC equipped with the appropriate NI LabVIEW^® software [19]. The electrodes attached to the piezoelectric layers of the studied devices are disconnected in the performed experiments in order to remove the influence of the resistive load on the response of the device via the mentioned forward and backward piezoelectric coupling effects.

The measurements are performed by subjecting the free end of the optimized PEH to impact excitation and letting the device oscillate at its mechanical eigenfrequency. The oscillations of the free end, i.e., the modal responses, are then measured by using the laser vibrometer, while the first eigenfrequency is assessed via the NI LabVIEW^® software. The clamping force applied to the piezoelectric layers of the studied devices is controlled by carefully tightening the two clamping bolts with a 1.5 Nm (± 6 %) torque measured by using a micro-torque wrench. The thus obtained experimental first eigenfrequencies $f_1$ for all the studied optimised PEH shapes, together with their respective standard deviations, are listed in Table 1.

Fig. 3a) Experimental setup: optimized PEH (1), clamping mechanism (2), laser vibrometer (3), vibrometer control and DAQ (4); b) detail: clamped optimized PEH; c) setup schematic representation. Photos were taken by Petar Gljušćić in May 2022 in the Precision Engineering Laboratory of the Department of Mechanical Engineering Design at the University of Rijeka, Faculty of Engineering, Rijeka, Croatia

a)

b)

c)

2.2. Plucking excitation

The experimental setup designed for characterizing the coupled electromechanical response of the optimised PEHs while enduring plucking excitation is schematically represented in Fig. 4(a). The setup (shown in detail in Fig. 4(b) and 4(c)) consists of 3D printed clamping mechanisms (1) and rotating plectra (2) plucking the various optimized harvesters (3) via a purely mechanical (i.e., not magnetic) plucking mechanism. This ensures avoiding possible dampening effects of the magnets close to the PEHs’ free ends due to their steel substrates [12]. The thus excited PEHs generate output voltages, which are measured by using an Agilent^® DSO-X 2012A oscilloscope paired with a variable resistance box (4) [12]. The resistance box simulates in this case the resistive load of an electrical load (e.g. the sensor) coupled to the PEH transducer, and it is set at the value of the optimal load resistance of the respective energy harvester shape. The initial displacement of the free end, required for later numerical analyses is, in turn, assessed via the mentioned Metrolaser^® Vibromet 500V laser doppler vibrometer (5) [12].

Fig. 4a) Experimental setup schematic representation; b) setup detail: clamping mechanism (1), rotating plectra (2), optimized PEH (3); c) setup detail: DAQ with resistance box (4) and laser vibrometer (5) [12]. Photos were taken by Petar Gljušćić in May 2022 in the Precision Engineering Laboratory of the Department of Mechanical Engineering Design at the University of Rijeka, Faculty of Engineering, Rijeka, Croatia

a)

b)

c)

The voltage outputs generated by the optimized PEHs subjected to plucking excitation are listed in Table 2 in terms of the maximal peak-to-peak and average voltages as calculated for the first two and five oscillations respectively. Due to the complexity of the plucking mechanism, the initial deflection of the free end ${\delta }_z$ is heavily influenced by the shape and stiffness of both the PEH and the plectrum (resulting from the nonuniform material deposition and delamination during the respective 3D printing process), as well as by the plucking speed, and cannot thus be accurately controlled or predicted in the herein used setup, resulting in different ${\delta }_z$ values for each experimentally studied PEH shape [14]. Moreover, the mechanical properties (i.e., stiffness) of the piezoelectric layers is affected by the electrical load applied to the harvester via the piezoelectric coupling effects as well [12, 14].

3.1. Modal responses

The FE analysis is utilized first to obtain the modes of vibration and the respective eigenfrequencies of the energy harvesters, providing inter alia the indispensable input values for the subsequent coupled transient analyses [20-21]. Only the first vibration mode is considered in this work, as it results in the largest deformations of the vibrating structure, and therefore generates the highest charge (voltage) in the piezoelectric layers [16, 22]. In order to obtain the uncoupled modal responses, the piezoelectric coefficient $e_{31}$ is set to zero in FE model’s material properties of the piezoelectric layers [7, 16]. As per ANSYS^® guidelines for large and symmetric eigenvalue problems, the block Lanczos method, along with the sparse direct matrix solver, are selected for the extraction of the first flexural vibration mode [23]. The models of the studied optimised PEH devices are then clamped at one end by setting the displacement of the top and bottom nodes within the clamping area to zero, and the required number of modes to extract as well as the desired frequency range are set. Bearing in mind the aimed balance between the accuracy of the results and the employed computational times [13, 15, 23, 24], a sensitivity analysis, based on gradually varying the density of the mesh by increasing the element edge length from 0.5 mm up to 1.75 mm, with 0.25 mm increments, is then performed.

The effect that the used type of the finite elements has on the accuracy of the model is concurrently studied as well. Two different finite element forms are therefore considered: the hexahedral (brick or cube) and the tetrahedral elements’ form. The PEHs’ piezoelectric layers are modelled by using the standard ANSYS^® 3D coupled-field solid finite element SOLID226, suitable for modelling piezoelectric, piezoresistive and thermoelectric materials, having 20 nodes and up to 6 DoFs per node. The SOLID186 ANSYS^® 3D structural solid element, with 20 nodes and 3 DoFs per node, is, in turn, employed for the substrate [23]. Two different element bonding methods available in ANSYS^® were analysed in a previous study, allowing to establish that their variation does not result in a significant effect on the FE model accuracy; the quicker and simpler method of “gluing” neighbouring volumes is therefore used [12-13]. The described modal analyses are employed to generate the modal responses of all the studied optimized PEH shapes and their respective first flexural vibration modes. Examples of the numerically obtained results are displayed in Fig. 5. The attained first eigenfrequencies $f_1$ are thus assessed at different mesh densities and element forms. The numerically attained first eigenfrequencies for the different optimized PEH shapes, obtained by using hexahedral finite elements of varying edge lengths, are listed in Table 3, while those obtained by using tetrahedral elements are listed in Table 4.

Fig. 5Numerically assessed first flexural vibration modes for the optimized PEH shapes: a) trapezoidal, b) inverted trapezoidal, c) notched, d) trapezoidal with stress concentrators and e) inverted trapezoidal with stress concentrators

a)

b)

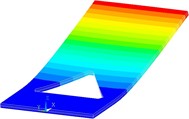
c)

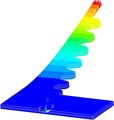
d)

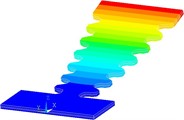
e)

3.2. Transient responses

Transient FE analyses employed in this work are aimed to simulate the plucking excitation of the piezoelectric energy harvesters. In order to attain the voltage outputs, a coupled FE model with the same geometry and material properties as in the modal analysis is used. The mesh sensitivity analysis is then performed by using the same element types as in case of the modal analysis (i.e., SOLID226 and SOLID186) across the same element edge length range (from 0.5 mm up to 1.75 mm, with 0.25 mm increments). The electromechanical coupling is carried out by setting the effective transverse piezoelectric coefficient, corresponding to the coupling mode 31 of a cantilever-based PEH under a bending load with the force applied perpendicular to the material poling direction, to the PZT-5A piezoelectric material value $e_{31}=$ – 10.4 C/m² derived from the data obtained from the supplier of the original rectangular bimorph cantilevers [13], as well as by introducing a finite element acting as a variable resistor, i.e., simulating the applied resistive loads, and connecting it to the nodes on the elements forming the piezoelectric layers [12, 14]. The load resistance itself is set to the optimal value for the respective PEH shape [14].

The PEH model is again clamped at one end while an initial displacement, equal to that measured in the respective experiments, is gradually applied to the edge of the free end. The deflected free end is then released by setting the displacement value in the next loading time step to zero, allowing the harvester to freely oscillate at its eigenfrequency [12, 14].

The resulting numerically obtained transient responses for all the studied optimized PEH shapes, assessed at different mesh densities and element forms, are listed in Tables 5 and 6. The results are represented both as maximal peak-to-peak voltages $U_{p-p}$ (Fig. 6(a)) generated in the first oscillation of the PEH, and as the average voltages $U_{ave}$ calculated for the first five oscillation cycles (Fig. 6(b)), where the majority of the PEHs’ power output is generated.

Fig. 6Graphical representation of a) the maximal peak-to-peak and b) average voltage calculated over the first five PEHs’ oscillations

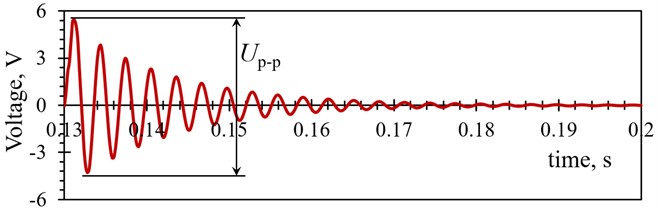
a)

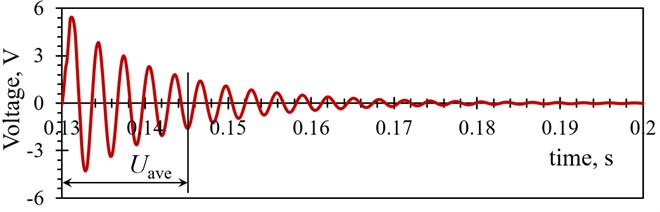
b)

4.1. Modal results

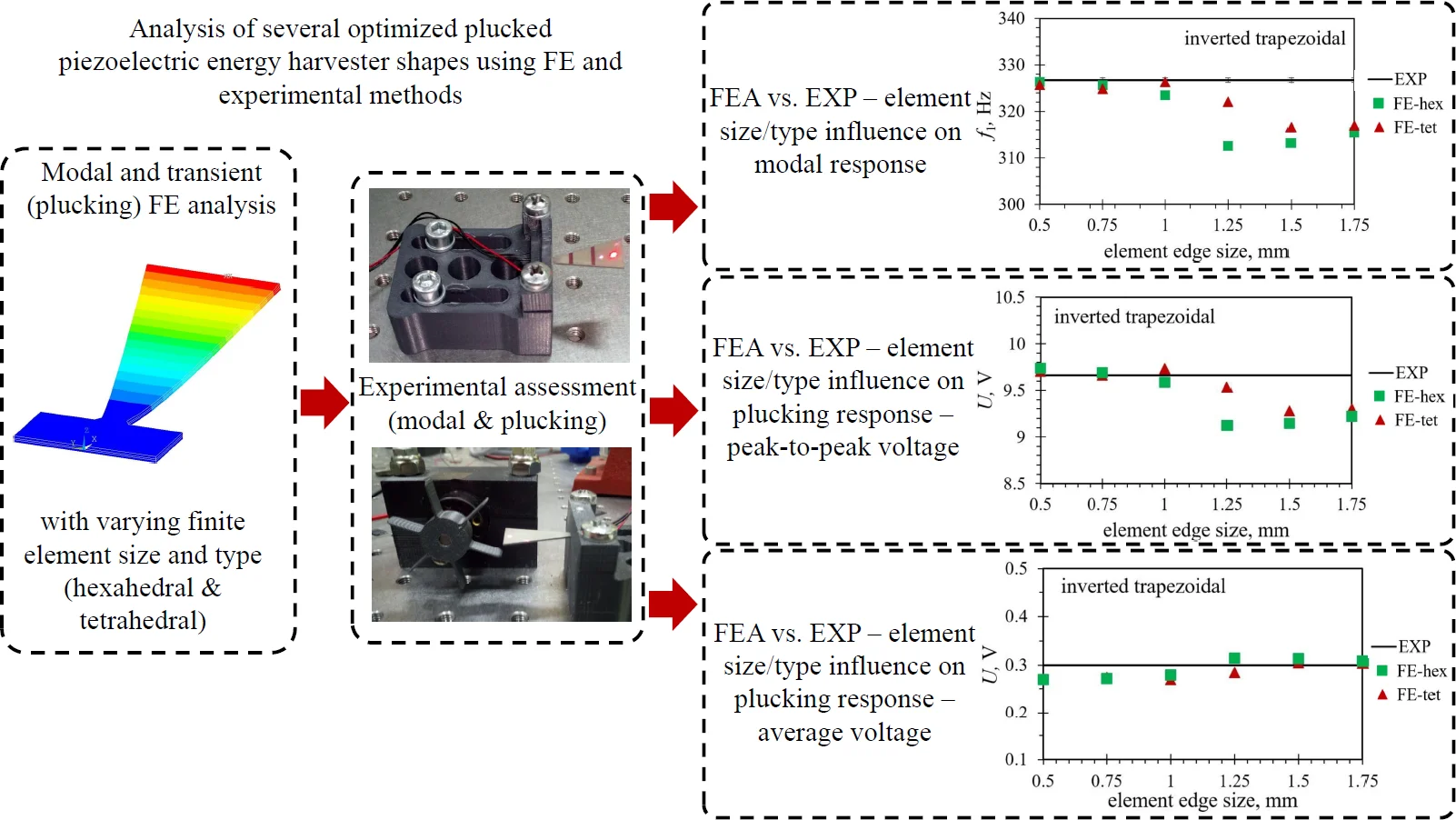
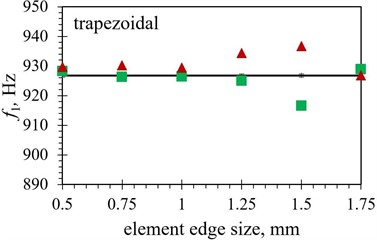
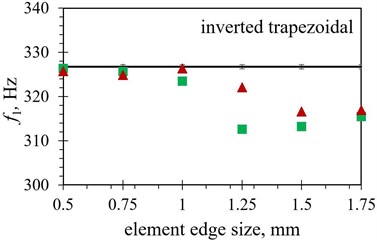
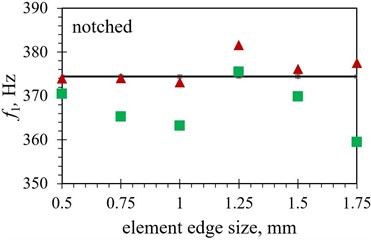
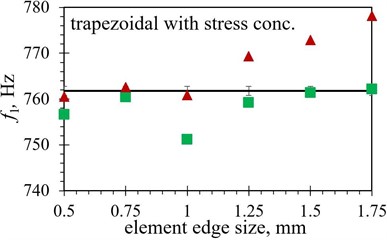
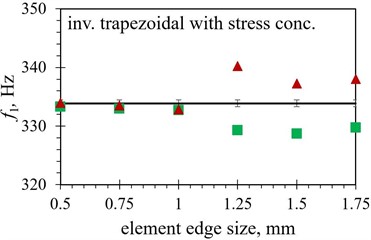
When the modal responses of Tables 2 and 3 are observed, a notable difference in eigenfrequency values can be observed between the models obtained by using the hexahedral and those based on using tetrahedral finite element forms. The absolute difference ranges from as little as < 0.1 % for several shapes using a finer mesh up to ~ 5 % for the inverted trapezoidal shape. This could imply that the correct selection of the element is more important in some geometries than in the others, as the average difference in eigenfrequency values between the two considered element forms is found to be ~ 0.7 % in the case of the trapezoidal shape, while it increases to ~ 2.5 % when the notched shape is analysed. The modal response results obtained by using both considered element forms are graphically displayed in Fig. 7 in comparison with the experimental values. As it can be seen from the figures, the tetrahedral elements seem, overall, to be better suited to model the complex studied optimised PEH geometries. In most cases, most prominently for the notched shape, the hexahedral element results start to diverge from the experimental values even if the mesh is fairly dense, i.e., at element edge lengths of 0.5 mm, while the tetrahedral results follow the experimental values more accurately.

In terms of the element edge length, generally a relatively close match of the FE values with the experimental results can be achieved with tetrahedral elements up to 1 mm, or even, in some cases, 1.25 mm, while more prominent fluctuation can be observed for longer edge lengths. Even if in some of these cases, notably of the 1.75 mm elements applied to both trapezoidal shapes, the use of larger elements results in a very close match with experimental data, such a model should be thoroughly assessed in terms of its stability.

The hexahedral elements exhibit, in turn, a fairly close match to the experimental values with element edge lengths up to 1 mm only in case of both trapezoidal shapes (1.25 mm in case of the straight edged one). When more complex optimised PEH geometries are investigated, the mentioned limitation of hexahedral elements hinders a comprehensive analysis, as only elements of 1 mm or less can be used, most apparently when the notched and the inverted shape with stress concentrators are observed.

In order to illustrate the influence of the element type on the model accuracy, the average difference between the FE eigenfrequency values obtained via the two used element forms and those assessed experimentally is listed in Table 7. A clear advantage of using tetrahedral elements can thus be observed, with differences smaller than 1.5 % (generally < 0.7 %), except for the trapezoidal shapes, which seem to favour the hexahedral elements, displaying an average difference of 0.17 % vs. 0.47 % for the straight edged shape and 0.43 % vs. 0.73 % for the shape with stress concentrators.

Fig. 7Numerical first eigenfrequency values f1 obtained with different finite element forms with varying edge lengths for the optimized PEH shapes, compared to the respective experimental data: a) trapezoidal, b) inverted trapezoidal, c) notched, d) trapezoidal with stress concentrators and e) inverted trapezoidal with stress concentrators

a)

b)

c)

d)

e)

4.2. Transient results

When the transient results are considered, a pattern similar to that seen in the modal case can be observed. The comparison is graphically displayed in Figs. 8 and 9 for the maximal peak-to-peak and the average output voltages respectively. Tables 6 and 7 show, in turn, the average difference between the numerical and experimental results in terms of the maximal peak-to-peak and the average output voltages obtained by using the two different element forms.

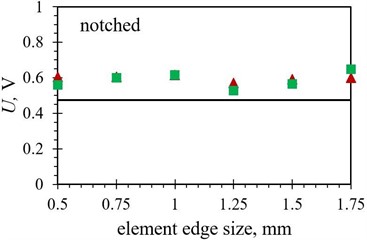
The absolute difference between the results of the experimental and the FE analyses, in terms of the maximal peak-to-peak output voltages, ranges from as little as < 0.1 % for the straight edged inverted trapezoidal shape, up to ~ 8 % for the notched shape. If the average voltage is considered, a notably larger discrepancy can be seen between the experiments and FE analyses, ranging from ~ 1.6 % for the inverted trapezoidal shape up to ~ 26 % in case of the notched shape. Such an occurrence, i.e., the inability of the numerical model to accurately predict the behaviour of the oscillating PEH throughout its oscillating period could be attributed to the slight shift in the oscillation frequency (as discussed in Subsection 4.1.), the non-ideal modelling of the clamping area, as well as the inaccuracies present in assessing the FEA damping coefficients.

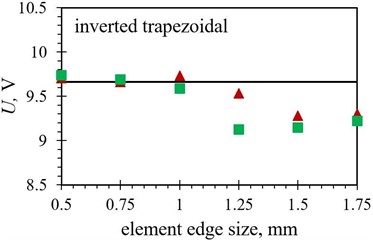
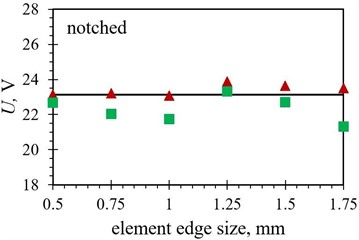
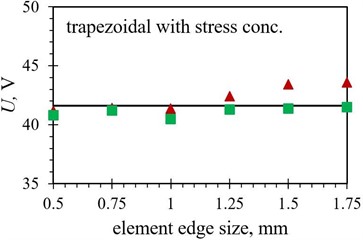
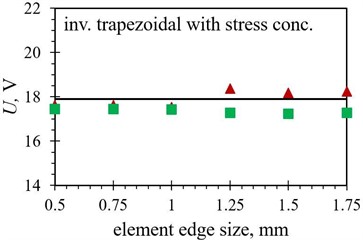
Fig. 8Numerical maximal peak-to-peak output voltage values obtained with different finite element forms with varying edge lengths for the optimized PEH shapes, compared to the respective experimental data: a) trapezoidal, b) inverted trapezoidal, c) notched, d) trapezoidal with stress concentrators and e) inverted trapezoidal with stress concentrators

a)

b)

c)

d)

e)

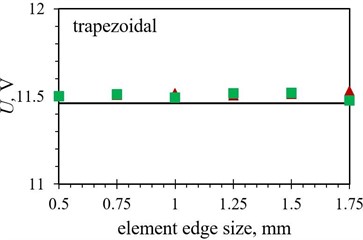
As it can be observed in Figs. 8 and 9, the tetrahedral elements appear to generally be more suitable for modelling the considered complex optimised PEH geometries, except, similar as in the case of the modal responses, for both the trapezoidal shapes, where the usage of hexahedral elements results in more accurate results in terms of the maximal peak-to-peak output voltages. This could be attributed to the relatively wide and homogenous trapezoidal area near the clamping base (where most of the charge is generated), which might favour brick elements. In general, the maximal peak-to-peak voltage results, obtained by using both tetrahedral and hexahedral elements, follow fairly accurately the experimental data up to an element edge length of 1.25 mm. The two exceptions are the straight edged inverted trapezoidal shape, where a significant divergence occurs at the 1 mm edge length, and the notched shape, where the hexahedral element results start to deviate already at an element edge length of 0.75 mm.

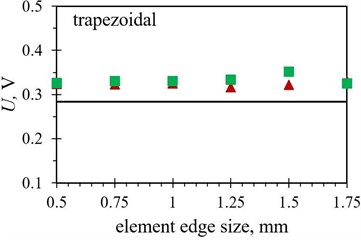
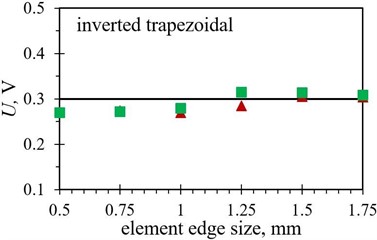
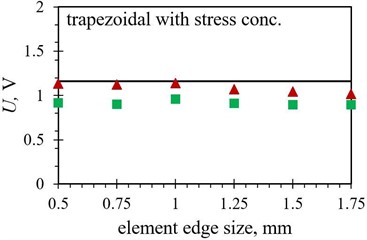
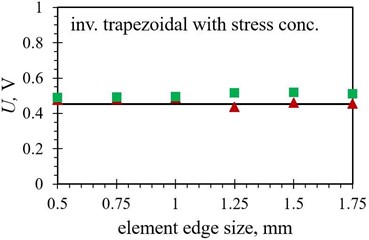
Fig. 9Numerical average output voltage values, measured over the first five PEH oscillations, obtained with different finite element forms with varying edge lengths for optimized PEH shapes, compared to the respective experimental data: a) trapezoidal, b) inverted trapezoidal, c) notched, d) trapezoidal with stress concentrators and e) inverted trapezoidal with stress concentrators

a)

b)

c)

d)

e)

In terms of the average output voltages, the overall divergence from the experimental results is significantly more pronounced for all the studied PEH shapes due to the above-mentioned issues. The trend exhibited by the two datasets (hexahedral vs. tetrahedral) seems, however, to be very similar.

As it was the case with the modal results, the importance of selecting the appropriate element form for modelling a specific optimised PEH geometry is apparent in the transient analyses as well, shown by the average differences listed in Table 8, where an average difference in the maximal peak-to-peak voltage values between the two considered element forms is found to be smaller than 0.5 % in case of the trapezoidal shape with straight edges, increasing to ~ 3 % for the inverted trapezoidal shape with stress concentrators. The tetrahedral elements show again a slightly better performance (differences of ~ 2 % or less) for most of the studied PEH shapes, except for the two trapezoidal ones, where hexahedral element exhibit slightly better results (0.38 % vs. 0.46 % and 1.25 % vs. 2.15 % respectively).

When the average voltage values, listed in Table 9, are in turn observed, the previously mentioned overall smaller deviations between the diverse element forms can be seen (apart for the trapezoidal shape with stress concentrators), whereas the divergence from the experimental results is significantly more pronounced. It should be also noted here that the required computational times, typically insignificant for modal analyses of this scale and already much longer in the case of the transient analyses, vary considerably depending on the element edge length, ranging from several minutes per simulation in case of elements with an edge length of 1 mm and above, up to several hours for finer meshes using 0.5 mm and 0.75 mm elements. The influence of element form is negligible in this frame, while the volume of the studied PEH, predictably, does somewhat affect the time required to solve the larger number of equations.