Abstract
Metamaterials are materials having artificially tailored internal structure and unusual physical and mechanical properties. Due to their unique characteristics, metamaterials possess great potential in engineering applications. This study proposes a tunable metamaterial for the applications in acoustic isolation. Therefore, a stopband in the dispersion curve can be created because of the energy gap. For the conventional metamaterial, the stopband is fixed. Although the metamaterial with tunable characteristics has been proposed in the literature to extend its working stopband, the efficacy is usually compromised. In this study, cantilevers of tunable shape memory materials (SMM) via controlled phase transformation are incorporated into the metamaterial plate. Its theoretical finite element formulation for determining the dynamic characteristics is established. The effect of the configuration of the SMM cantilever absorbers on the metamaterial plate for the desired stopband in wave propagation is simulated by using finite element model and a commercial multi-physics software. The result demonstrates the tunable capability on the stopband of the metamaterial plate under different activation controls of the SMM absorbers, and shows the ability to trap the vibration at the designed frequency and prevent vibration wave from propagating downstream in different absorber arrangements and alloy phases. It should be beneficial to precision machinery and defense industries which have desperate need in vibration and noise isolation.
Highlights
- An acoustic metamaterial plate with attached array of vibration absorbers made of tunable SMA cantilevers is analyzed using coupled finite element model.
- Working frequency of the metamaterial plate is tunable between 1482 Hz and 2702 Hz with achievable increase in sound transmission loss around 15 dB, comparing to the base plate.
- Selected activation of the SMA cantilevers can still have similar sound transmission loss while with less energy consumption for actuation.
1. Introduction
In the modern society, the better control in vibration and noise gains more and more attentions both environmentally and industrially. Barrier materials are frequently employed to avoid or isolate the transmission of noise between two adjacent spaces. Conventionally, fibrous or porous materials constitute the major roles in the noise isolation of machinery. According to the mass law in acoustics, to increase the sound transmission loss for achieving better noise isolation, the use of thicker insulation is unavoidable [1]. Thicker insulation usually means heavier construction or more restriction in application.
Apart from the conventional approach, metamaterials in relevant applications provide other promising choice recently. Metamaterial is a class of artificially designed and manufactured materials with special inner structure. The sub-wavelength characteristic structure to provide the resonance with the incident wave-like excitation can offer unique dynamic properties which are impossible to be obtained from natural materials, such as negative mass density, negative material modulus, negative refractory index and negative Poisson’s ratio, etc. These unique properties can reflect on the material’s superior performances on electromagnetic shielding, acoustic isolation and vibration reduction [2-5]. Specifically, acoustic metamaterials possess the aforementioned intrinsic resonant structure which vibration nature can be tuned to activate the different stopbands in response to the noises at different frequencies [6-13].
The acoustic metamaterials proposed in the literature are mostly in a plate-like form with intrinsic [14, 15] or extrinsic [16, 17] resonant structures. More specifically speaking, intrinsic metamaterial has the resonant substructure built inside the plate-like structure while the extrinsic one has the resonant substructure appended on the base plate. From the acoustic attenuation prospective, both types of acoustic metamaterials can have similar sound transmission losses around 40-50 dB. However, the intrinsic metamaterial has fixed internal structure once it is manufactured. It may be more concise in appearance, but it has little flexibility to adapt to different application environments by changing its number or configuration of the resonant substructures as demanded. On the contrary, the extrinsic metamaterial may install the resonant substructures as required for a specific application or modify the existing configuration according to the required optimization.
Acoustic metamaterial has received quite much attention in recent researches for noise control. The sub-wavelength microstructure provides the preferred transmission path for acoustic wave and traps the acoustic energy. Although it is effective for the resonant wave, the substructure with single dynamic characteristics limits the narrow bandwidth of its stopband. The low bandwidth consequently hinders its wide applications in most situations. Therefore, designs of acoustic metamaterials with tunable stopband have been proposed recently. For examples, the use of piezoelectric material [18-26], mechanically controlled loading and deformation [27-29], actuation by magnetic field [30], hydraulic power [31], and temperature [32], etc. have demonstrated successfully the tunability of the stopband and the applicability in a variety of industrial applications.
In the other tunable design of acoustic metamaterial, shape memory materials including shape memory alloy (SMA) and shape memory polymer (SMP), are adopted in the actuator implementation. The shape memory effect and the superelastic characteristics of SMAs can be applied in the design actuators having extensional, flexural, or torsional loading capability. Their realizations result in the configurations of helical spring, torsional spring, linear actuator, cantilever and torsional rod, etc [33-35]. The adoptions of SMA actuator in the semi-active metamaterial structure through the change in stiffness [36-40] and superelasticity [41-44] upon the temperature-activated phase transformation have the merits of easy construction, low maintenance and high reliability.
In this study, a class of resonant substructure composed of nitinol wire in double-cantilever configuration is proposed. This acoustic metamaterial was constructed by attaching the SMA double-cantilever units on top of an aluminum plate. The arrangement of the double-cantilever units over the plate and the switch between martensite and austenite phases of the SMA wires can provide an acoustic metamaterial design with tunability in the stopband. A finite element simulation using COMSOL® was employed to demonstrate the feasibility of this design.
2. Design of SMA Absorber
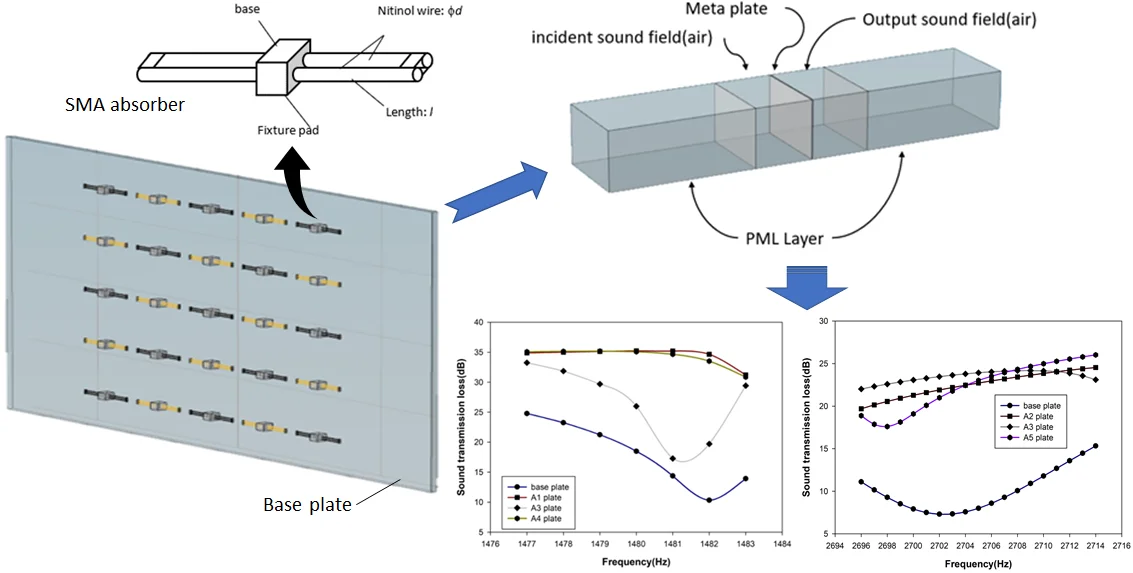
Fig. 1 presents the schematic diagram of the proposed resonant unit composed of double-cantilever SMA wire. The double-cantilevered configuration was adopted because its second natural frequency was nearly four times larger than its fundamental one. Thus, it is more realistic in assuming the double-cantilever unit as a single degree-of-freedom system for the interested frequency domain. It must be mentioned that the symmetric arrangement of the double-cantilever on either side of the base is to impose only vertical loading on the base plate with little moment. Moreover, the symmetric design also increases the mass effect of the resonant unit to absorb more kinetic energy in vibrational environment. The two separated SMA wires with connection at the free end was intended to form an electrical circuit for conducting the control current. The joule heating from the applied electric current was able to raise the SMA temperature to induce the austenitic transformation while the natural convection was used to cool the temperature for the martensitic transformation. If necessary, a forced convectional cooling can be imposed with cooling fan. As an example, Table 1 lists the mechanical properties of an SMA nitinol [45, 46]. It is seen that the modulus of elasticity increases from 24 GPa to 76 GPa as the phase of nitinol changes from martensite to austenite. Without noticeable change in other property and dimension parameters, the theoretical fundamental frequency of the double-cantilever unit is raised from 1499 Hz to 2688 Hz by heating the nitinol from martensite to austenite.
Fig. 1The schematic diagram of a double-cantilever SMA resonant unit proposed in this study
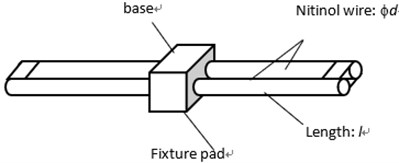

Table 1The mechanical properties of a typical SMA nitinol [45, 46]
Property | Magnitude |
Mass density | 6450 kg/m3 |
Tensile strength | 754-960 MPa |
Yield strength | 560 MPa |
Poisson’s ratio | 0.3 |
Modulus of elasticity (martensite) | 24 GPa |
Modulus of elasticity (austenite) | 76 GPa |
Percent elongation | 15.5 % |
Shear strength | 28.8 GPa |
3. Simulation analysis
3.1. Sound transmission loss
For the one-dimensional transmission of an acoustic wave with frequency ω from a fluid having mass density of ρ1 and speed of sound c1 into a solid having thickness of L and speed of sound c2, and then into a fluid having the same properties as the first fluid, the sound transmission loss (STL) for the acoustic wave to pass through the solid can be defined as [1, 47, 48]:
Physically, STL denotes the ratio of sound pressure intensities between output side and input side of the solid medium in decibel (dB) measurement. In the real-world applications, the sound transmission is hardly one-dimensional. Therefore, a numerical analysis based on finite element method was adopted in this study. The STL was calculated by using the sound pressure intensities obtained from the numerical simulation.
For the finite element simulation on the acoustic wave transmission from fluid domain through solid separation into other fluid domain, in addition to the dynamics in both fluid and solid regions to be considered, the fluid-solid interaction should also play a crucial role. Therefore, the finite element software COMSOL Multiphysics was adopted in this study. Fig. 2 presents the domain configuration model used in the finite element simulation. The selection of this configuration refers to the other study adopted in the literature [39]. The associated parameters for this model are listed in Table 2.
As seen in Fig. 2, the plate under consideration was a 0.3 m width, 0.2 m height, and 3 mm thickness in dimensions with fixed displacement boundary conditions along its edges. At 0.2 m away from the tested plate both in the upstream and downstream directions, there are the defined planes to collect the input and output acoustic waves inside the duct. On the front and back ends of the air duct, perfectly matched layers (PML) were applied to eliminate the effect from the acoustic refection on the walls of the analysis domain. The input acoustic wave was 1 Pa in the amplitude of sound pressure with different specified frequencies. The average amplitude of the sound pressure on the aforementioned plane downstream was collected to calculated the sound transmission loss through the tested plate.
Fig. 2The domain configuration used in the finite element simulation
Table 2The parameters for the finite element model used in calculating the acoustic wave transmission through the separation plate
Parameter | Magnitude | |
Mass density of air | 1.2 kg/m3 | |
Sound speed of air | 343 m/s | |
Dimensions of air duct | Length | 0.4 m |
Width | 0.3 m | |
Height | 0.2 m | |
Boundary conditions | Matched boundary | |
Input amplitude of sound pressure | Amplitude | 1 Pa |
Perfectly matched layer | Length | 0.5 m |
Width | 0.3 m | |
Height | 0.2 m | |
4. Results and discussion
4.1. The plain aluminum plate
As a benchmark for the study of the sound transmission loss through the tested plate, a plain aluminum plate without installation of the double-cantilever unit was simulated first. A sweep sine of acoustic pressure with 1 Pa amplitude and different frequencies was imposed at the left end of the air duct. Because of the symmetric nature of the rectangular cross-section of the air duct, it was suspected that only the symmetric mode of the tested plate would only be excited if the input acoustic wave was also symmetric. Therefore, the response of the system to an incident acoustic wave with 45° to the normal of the tested plate was also simulated.
Before the further discussion on the simulation results, the convergence of the finite element analysis should be checked. Table 3 list the first 12 resonance frequencies of the plain aluminum plate with all fixed boundary conditions along its edges. The element size of 1.2 mm was employed in the discretization using tetrahedral elements. These results show that the finite element simulation was able to give a reasonable representation of the physical system.
Fig. 3 shows the transient acoustic wave incident to the aluminum plate at certain frequency. The right figure illustrates the case with normal incident wave while the right one with oblique wave at 45°. They also demonstrate that the use of PML was able to diminish the reflective wave during simulation.
Table 3The first 12 resonance frequencies of the plain aluminum plate with all fixed boundary conditions
Mode | Finite element analysis (Hz) | Analytical solution (Hz) [49] |
1st | 504.69 | 503.13 |
2nd | 778.38 | 777.09 |
3rd | 1234.20 | 1232.0 |
4th | 1240.00 | 1239.7 |
5th | 1488.00 | 1487.8 |
6th | 1876.60 | 1878.6 |
7th | 1920.40 | – |
8th | 2333.80 | – |
9th | 2530.40 | – |
10th | 2580.10 | – |
11th | 2680.20 | – |
12th | 2996.90 | – |
Fig. 3The illustration of the incident acoustic wave simulated at different orientations
Fig. 4Simulation of the sound transmission loss spectra through plain aluminum plate for the normal and oblique incident acoustic waves
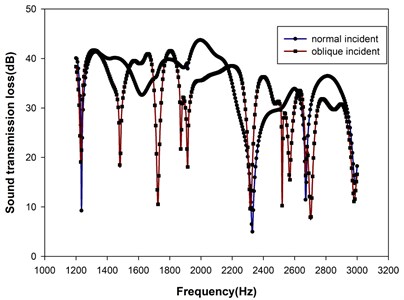
Fig. 4 presents the simulated sound transmission loss spectra through plain aluminum plate for the normal and oblique incident acoustic waves. For the normal incident wave, there were four dips in the STL at 1234, 2334, 1680 and 2997 Hz, respectively, over the frequency span studied. On the other hand, for the oblique incident wave, significant drops occurred at nearly all the resonance modes as indicated in Table 2. At each resonant frequency of the dividing plate, the incident wave excites the plate into resonance and subsequently, the kinetic energy of the plate transmits downstream to the output end of the air duct. Because the normal incident wave is theoretically unable to excite the plate into resonance of antisymmetric mode, the kinetic energy at that resonance frequency is obstructed mostly from propagating downstream. Hence, STL is still high for that resonance frequency. To circumvent this difficulty, only the simulation using 45° oblique incident wave was employed afterwards to investigate all possible transmission modes.
4.2. The metamaterial plate with double-cantilever resonance units
Fig. 5 presents a metamaterial plate on which 25 equally spaced double-cantilever resonance units were installed. Because each SMA resonance unit can be tuned into martensite or austenite phase by controlling its temperature, the resonance frequency of the unit can be switched between 1482 Hz (martensite) and 2702 Hz (austenite).
Fig. 5The schematic diagram of the metamaterial plate with 25 equally spaced double-cantilever resonance units installed on the aluminum plate

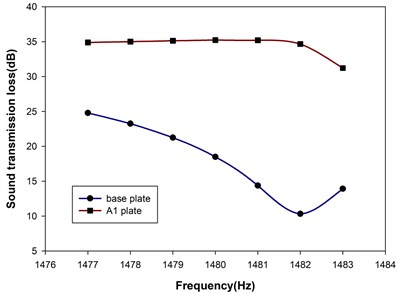
For all SMA resonance units were in martensitic phase, the metamaterial plate was denoted as A1 plate in short. The STL spectrum of this A1 plate near the resonance frequency around 1482 Hz is shown in Fig. 6, along with that of aluminum base plate for comparison. As seen from Table 3, excitation frequency at 1482 Hz was close to the resonance frequency of the base plate at 1488 Hz. The base plate was gaining resonant vibration in displacement amplitude which transmitted the kinetic energy to the other side of the base plate and passed on to the air downstream. The more resonant vibration of the plate, the more kinetic energy passing on downstream. Thus, STL reached a minimum at resonance frequency of the base plate, i.e. 1482 Hz which was a little lower than 1488 Hz because of the damping and inertia effect of air fluid interaction with the plate. As the air duct was separated by the A1 plate, STL remained nearly unchanged over the frequency span. The resonance units of the metamaterial plate were able to absorb the vibration energy of the base plate and kept the base plate in low vibration amplitude. Therefore, the pass of the kinetic energy was obstructed effectively by the metamaterial plate and STL maintained its high level.
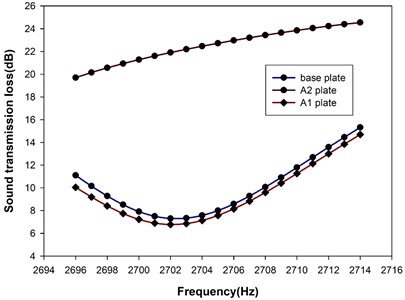
It is understandable that external acoustical excitation can have different frequency spectrum, such as the machinery can be operated at different rotational speeds. The tunability on the operational frequency of the metamaterial plate can be essential for these applications. Therefore, if all the SMA resonant units were heated up to austenitic phase, the resonance frequency of the SMA double-cantilever could be raised accordingly to 2702 Hz. And the metamaterial plate is denoted as A2 plate for convenience. Fig. 7 presents the STL spectra for the A2, A1 and base plates over the frequency span near 2702 Hz. As expected from previous discussion, the A2 plate had high level of STL over the frequency span because the SMA resonance units were able to trap the vibrational energy from propagating downstream. Although the base plate was not in resonance vibration (Table 3), the induced structural vibration due to the incident acoustic wave was able to propagate the acoustic energy downstream. Therefore, the STL was relatively low. It should be noted that the STL for A1 plate was similar to the base plate. The superior STL performance of A1 plate in Fig. 6 did not carry on to this frequency span. This apparently demonstrates the need for active tuning the operational frequency of the metamaterial plate for excitation with changing frequency.
Fig. 6The STL spectrum of the A1 plate near the resonance frequency around 1482 Hz, along with that of aluminum base plate for comparison
From the previous results, it is noted that as the SMA resonance units are excited in their resonance frequency, the vibration of the metamaterial plate can be significantly reduced by passing on the kinetic energy to the absorbers. The acoustic energy in the upstream can hardly propagate into the downstream through this metamaterial plate. In other words, the metamaterial plate has high STL. This mechanism forms a stopband of the metamaterial plate in the transmission of the acoustic wave. The activation of the SMA resonance units from martensite to austenite raises the frequency stopband of the proposed metamaterial plate. In general, if the SMA double-cantilever is activated with partial martensite and partial austenite in the microstructure, the combination of both phases can tune the material’s elastic modulus between the two extremes, the low martensite and the high austenite [50]. However, the hysteresis and nonlinearity in the control of SMA actuator usually complicates the implementation. Therefore, it is not pursued in this study for now.
Fig. 7The STL spectrum of the A2 plate near the resonance frequency around 2702 Hz, along with those of aluminum base plate and A1 plate for comparison
4.3. The metamaterial plate with selectively activated SMA resonance units
The activation of the SMA double-cantilever resonance unit from martensite to austenite phase requires the raise of temperature. In term of joule heating, this consumes input electrical energy. To explore the possibility of reducing energy consumption in the operation of this metamaterial plate, the effect of partial activation among the SMA resonance units was investigated.
As the first attempt, only the alternating resonance units were activated to austenitic phase while the rest ones remaining in martensitic phase, as shown in Fig. 8 and annotated as A3 plate. The comparisons on the STL spectra near the two stopbands corresponding to the resonance frequencies of the martensitic and austenitic SMA units, respectively, are presented in Fig. 9. The STLs of A3 plate at 1482 Hz and 2702 Hz are 19.7 dB and 23.5 dB, which have 90.81 % and 221.82 % improvement comparing to the base plate. It should be noted that the STL at 1482 Hz for A3 plate was not so good as the A1 plate. Considering only half of the SMA resonance units were operating at this frequency, the lowering in STL than its fully operating A1 counterpart would be plausible. However, the STL at 2702 Hz of A3 plate showed an equivalent level of improvement as its fully operating A2 counterpart. The mechanism causes this difference should be explored further.
Fig. 8A3 plate with the SMA resonance units alternatively activated to austenitic phase (yellow colored) while the remaining ones in martensitic phase (black colored)
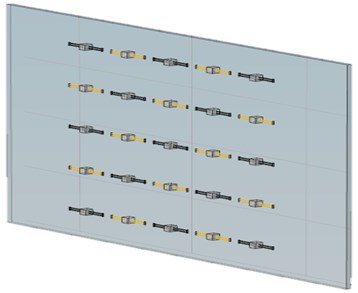
Fig. 9The STL spectra near the stopbands of different metamaterial plates
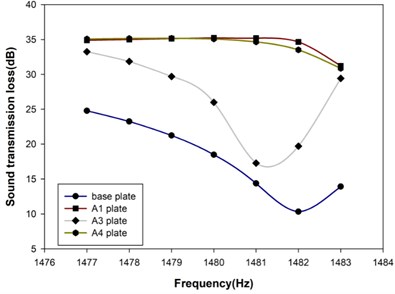
a) Stopband associated with martensitic SMA units
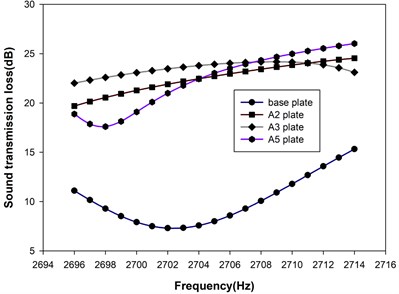
b) Stopband associated with austenitic SMA units
Fig. 10 presents the vibration mode shapes of the metamaterial plate at two different frequencies, corresponding to the resonance frequencies of the SMA unit at martensite and austenite phases, respectively. It is understood that the resonance unit located near the nodal lines receives less vibrational energy from the base plate and contributes less function in operation. On the other hand, those located near the region with large vibrational displacement can demonstrate more their functions. Therefore, the arrangement of SMA resonance units of A3 plate, as shown in Fig. 8, were more in active locations for the austenite ones at 2702 Hz than those martensite ones at 1482 Hz. More explicitly, there were 4 martensite units operating in large vibrational amplitude at 1482 Hz while 8 austenite units at 2702 Hz.
Fig. 10The mode shapes of the metamaterial plate at different frequencies
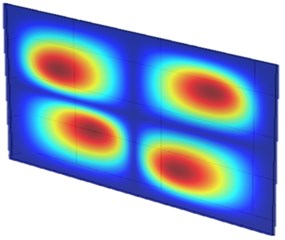
a) 1482 Hz
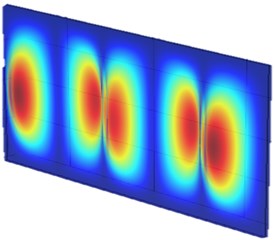
b) 2702 Hz
With this design methodology in mind, different activated configurations on the SMA resonance units were investigated further. Fig. 11 presents the partially activated metamaterial plates with austenite (yellow-colored) and martensite (black-colored) resonance units, which were named A4 plate and A5 plate, respectively. A4 plate had 8 SMA resonance units in martensite phase while the A5 plate had 5 units in austenite phase. The STL spectra of the A4 and A5 plates over the lower and higher frequency stopbands are also presented in Fig. 9. It is seen that the A4 plate had similar performance in STL as that of A1 plate while the performance of A5 in STL was more or less comparable to that of A2. The results indicate that with the knowledge of the vibrational mode shape at the targeted frequency, the controlled activation of the metamaterial plate can be operated in a more efficient fashion. Table 4 summarizes the STLs of different metamaterial plates and their improvements from the base plate. The numerical results show the proposed metamaterial plate can be effective in the application of acoustic insulation with tunable frequency capability.
Table 4The STL of the different metamaterial plates at two stopband frequencies
Item | Frequency | Base plate | A1 plate | A2 plate | A3 plate | A4 plate | A5 plate |
STL (dB) | 1482 Hz | 10.32 | 34.60 | 19.70 | 33.51 | ||
2702 Hz | 7.30 | 21.90 | 23.50 | 20.99 | |||
ΔSTL (dB) | 1482 Hz | – | 24.28 | 9.38 | 23.19 | ||
2702 Hz | – | 14.60 | 16.20 | 13.69 |
Fig. 11Partially activated metamaterial plates with austenite (yellow-colored) and martensite (black-colored) resonance units
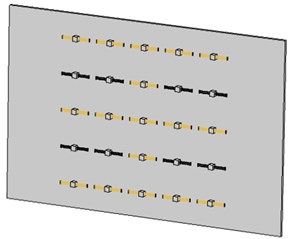
a) A4 plate
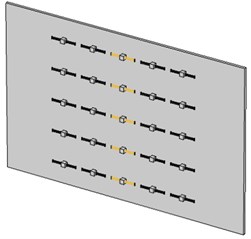
b) A5 plate
5. Conclusions
The sound transmission loss through a proposed tunable acoustic metamaterial plate design incorporating extrinsically added SMA resonance units has been investigated by using finite element simulation. The finite element analysis for an air duct divided by the metamaterial plate was carried out to calculate the sound transmission loss through the plate. With the dimensions of the double-cantilever resonance unit example, the operation frequency for the stopband of the metamaterial plate was capable of changing from 1482 Hz to 2702 Hz via controlling the SMA from martensite phase to austenite phase. With deployed 5×5 array SMA units, the metamaterial plate was able to increase the STLs from 10.32 dB to 34.60 dB and 7.30 dB to 21.90 dB at 1482 Hz and 2702 Hz, respectively. The SMA unit located near the region with larger vibrational displacement is more capable of absorbing the vibrational energy and reducing the plate vibration, and subsequently raising the STL. Therefore, selectively activating the SMA units according to the vibration mode shape of the metamaterial plate at the desired operational frequency can effectively reducing the energy consumption for this tunable acoustic insulation plate. Because the hysteretic effect of the SMA actuator in the transient transformation between martensite and austenite was not pursued yet in this study, the incorporation of hysteretic models, such as recently proposed in the literature [51, 52], can be topic for further study.
References
-
D. N. Manik, Vibro-Acoustics: Fundamentals and Applications. Boca Raton: CRC Press, 2017, https://doi.org/10.1201/9781315156729
-
A. Srivastava, “Elastic metamaterials and dynamic homogenization: a review,” International Journal of Smart and Nano Materials, Vol. 6, No. 1, pp. 41–60, Jan. 2015, https://doi.org/10.1080/19475411.2015.1017779
-
R. Zhu, X. N. Liu, G. K. Hu, F. G. Yuan, and G. L. Huang, “Microstructural designs of plate-type elastic metamaterial and their potential applications: a review,” International Journal of Smart and Nano Materials, Vol. 6, No. 1, pp. 14–40, Jan. 2015, https://doi.org/10.1080/19475411.2015.1025249
-
Z. Liu et al., “Locally resonant sonic materials,” Science, Vol. 289, No. 5485, pp. 1734–1736, Sep. 2000, https://doi.org/10.1126/science.289.5485.1734
-
J. B. Pendry, “Negative refraction makes a perfect lens,” Physical Review Letters, Vol. 85, No. 18, pp. 3966–3969, Oct. 2000, https://doi.org/10.1103/physrevlett.85.3966
-
L. Airoldi and M. Ruzzene, “Design of tunable acoustic metamaterials through periodic arrays of resonant shunted piezos,” New Journal of Physics, Vol. 13, No. 11, p. 113010, Nov. 2011, https://doi.org/10.1088/1367-2630/13/11/113010
-
J.-B. Li, Y.-S. Wang, and C. Zhang, “Tuning of acoustic bandgaps in phononic crystals with Helmholtz resonators,” Journal of Vibration and Acoustics, Vol. 135, No. 3, Jun. 2013, https://doi.org/10.1115/1.4023812
-
Y. Liu, X.-Z. Sun, W.-Z. Jiang, and Y. Gu, “Tuning of bandgap structures in three-dimensional Kagome-sphere lattice,” Journal of Vibration and Acoustics, Vol. 136, No. 2, Apr. 2014, https://doi.org/10.1115/1.4026211
-
M. R. Haberman and M. D. Guild, “Acoustic metamaterials,” Physics Today, Vol. 69, No. 6, pp. 42–48, Jun. 2016, https://doi.org/10.1063/pt.3.3198
-
L. Salari-Sharif, B. Haghpanah, A. Guell Izard, M. Tootkaboni, and L. Valdevit, “Negative-stiffness inclusions as a platform for real-time tunable phononic metamaterials,” Physical Review Applied, Vol. 11, No. 2, Feb. 2019, https://doi.org/10.1103/physrevapplied.11.024062
-
R. V. Craster and S. Guenneau, “Acoustic metamaterials,” in Springer Series in Materials Science, Dordrecht: Springer Netherlands, 2013, https://doi.org/10.1007/978-94-007-4813-2
-
T. J. Cui, D. R. Smith, and R. Liu, Metamaterials. Boston, MA: Springer US, 2010, https://doi.org/10.1007/978-1-4419-0573-4
-
S. Chen et al., “A review of tunable acoustic metamaterials,” Applied Sciences, Vol. 8, No. 9, p. 1480, Aug. 2018, https://doi.org/10.3390/app8091480
-
F. Langfeldt and W. Gleine, “Membrane – and plate-type acoustic metamaterials with elastic unit cell edges,” Journal of Sound and Vibration, Vol. 453, pp. 65–86, Aug. 2019, https://doi.org/10.1016/j.jsv.2019.04.018
-
T. Yamamoto, “Acoustic metamaterial plate embedded with Helmholtz resonators for extraordinary sound transmission loss,” Journal of Applied Physics, Vol. 123, No. 21, p. 215110, Jun. 2018, https://doi.org/10.1063/1.5025570
-
N. G. R. de Melo Filho, L. van Belle, C. Claeys, E. Deckers, and W. Desmet, “Dynamic mass based sound transmission loss prediction of vibro-acoustic metamaterial double panels applied to the mass-air-mass resonance,” Journal of Sound and Vibration, Vol. 442, pp. 28–44, Mar. 2019, https://doi.org/10.1016/j.jsv.2018.10.047
-
M. Jaberzadeh, B. Li, and K. T. Tan, “Wave propagation in an elastic metamaterial with anisotropic effective mass density,” Wave Motion, Vol. 89, pp. 131–141, Jun. 2019, https://doi.org/10.1016/j.wavemoti.2019.03.009
-
F. Casadei, T. Delpero, A. Bergamini, P. Ermanni, and M. Ruzzene, “Piezoelectric resonator arrays for tunable acoustic waveguides and metamaterials,” Journal of Applied Physics, Vol. 112, No. 6, p. 064902, Sep. 2012, https://doi.org/10.1063/1.4752468
-
S.-B. Chen, J.-H. Wen, G. Wang, and X.-S. Wen, “Tunable band gaps in acoustic metamaterials with periodic arrays of resonant shunted piezos,” Chinese Physics B, Vol. 22, No. 7, p. 074301, Jul. 2013, https://doi.org/10.1088/1674-1056/22/7/074301
-
A. Allam, A. Elsabbagh, and W. Akl, “Modeling and design of two-dimensional membrane-type active acoustic metamaterials with tunable anisotropic density,” The Journal of the Acoustical Society of America, Vol. 140, No. 5, pp. 3607–3618, Nov. 2016, https://doi.org/10.1121/1.4966627
-
Z. Li et al., “Broadband gradient impedance matching using an acoustic metamaterial for ultrasonic transducers,” Springer Science and Business Media LLC, Scientific Reports, Mar. 2017.
-
W. Akl and A. Baz, “Multicell active acoustic metamaterial with programmable effective densities,” Journal of Dynamic Systems, Measurement, and Control, Vol. 134, No. 6, Nov. 2012, https://doi.org/10.1115/1.4006619
-
W. Akl and A. Baz, “Experimental characterization of active acoustic metamaterial cell with controllable dynamic density,” Journal of Applied Physics, Vol. 112, No. 8, p. 084912, Oct. 2012, https://doi.org/10.1063/1.4759327
-
W. Akl and A. Baz, “Analysis and experimental demonstration of an active acoustic metamaterial cell,” Journal of Applied Physics, Vol. 111, No. 4, p. 044505, Feb. 2012, https://doi.org/10.1063/1.3686210
-
W. Akl and A. Baz, “Active acoustic metamaterial with simultaneously programmable density and bulk modulus,” Journal of Vibration and Acoustics, Vol. 135, No. 3, Jun. 2013, https://doi.org/10.1115/1.4023141
-
A. Allam, A. Elsabbagh, and W. Akl, “Experimental demonstration of one-dimensional active plate-type acoustic metamaterial with adaptive programmable density,” Journal of Applied Physics, Vol. 121, No. 12, p. 125106, Mar. 2017, https://doi.org/10.1063/1.4979020
-
K. J. B. Lee, M. K. Jung, and S. H. Lee, “Highly tunable acoustic metamaterials based on a resonant tubular array,” Physical Review B, Vol. 86, No. 18, Nov. 2012, https://doi.org/10.1103/physrevb.86.184302
-
P. Wang, F. Casadei, S. Shan, J. C. Weaver, and K. Bertoldi, “Harnessing buckling to design tunable locally resonant acoustic metamaterials,” Physical Review Letters, Vol. 113, No. 1, Jul. 2014, https://doi.org/10.1103/physrevlett.113.014301
-
F. Langfeldt, J. Riecken, W. Gleine, and O. Von Estorff, “A membrane-type acoustic metamaterial with adjustable acoustic properties,” Journal of Sound and Vibration, Vol. 373, pp. 1–18, Jul. 2016, https://doi.org/10.1016/j.jsv.2016.03.025
-
S. Xiao, G. Ma, Y. Li, Z. Yang, and P. Sheng, “Active control of membrane-type acoustic metamaterial by electric field,” Applied Physics Letters, Vol. 106, No. 9, p. 091904, Mar. 2015, https://doi.org/10.1063/1.4913999
-
Y. Jin, Y. Pennec, Y. Pan, and B. Djafari-Rouhani, “Phononic crystal plate with hollow pillars actively controlled by fluid filling,” Crystals, Vol. 6, No. 6, p. 64, May 2016, https://doi.org/10.3390/cryst6060064
-
B. Xia, N. Chen, L. Xie, Y. Qin, and D. Yu, “Temperature-controlled tunable acoustic metamaterial with active band gap and negative bulk modulus,” Applied Acoustics, Vol. 112, pp. 1–9, Nov. 2016, https://doi.org/10.1016/j.apacoust.2016.05.005
-
F. J. Fahy and P. Gardonio, Sound and Structural Vibration: Radiation, Transmission and Respons. Elsevier, 2007.
-
S. A. Hambric, S. H. Sung, and D. J. Nefske, Engineering Vibroacoustic Analysis: Methods and Applications. John Wiley & Sons, 2016.
-
J. Mohd Jani, M. Leary, A. Subic, and M. A. Gibson, “A review of shape memory alloy research, applications and opportunities,” Materials and Design (1980-2015), Vol. 56, pp. 1078–1113, Apr. 2014, https://doi.org/10.1016/j.matdes.2013.11.084
-
C.-Y. Lee and C.-A. Pai, “Design and implementation of tunable multi-degree-of-freedom vibration absorber made of hybrid shape memory helical springs,” Journal of Intelligent Material Systems and Structures, Vol. 27, No. 8, pp. 1047–1060, May 2016, https://doi.org/10.1177/1045389x15581519
-
D. Stoeckel, “Shape memory actuators for automotive applications,” Materials and Design, Vol. 11, No. 6, pp. 302–307, Dec. 1990, https://doi.org/10.1016/0261-3069(90)90013-a
-
T. Waram, Actuator Design Using Shape Memory Alloys. Hamilton, Ont.: TC Waram, 1993.
-
E. Rustighi, M. J. Brennan, and B. R. Mace, “A shape memory alloy adaptive tuned vibration absorber: design and implementation,” Smart Materials and Structures, Vol. 14, No. 1, pp. 19–28, Feb. 2005, https://doi.org/10.1088/0964-1726/14/1/002
-
Y. Mani and M. Senthilkumar, “Shape memory alloy-based adaptive-passive dynamic vibration absorber for vibration control in piping applications,” Journal of Vibration and Control, Vol. 21, No. 9, pp. 1838–1847, Jul. 2015, https://doi.org/10.1177/1077546313492183
-
M. A. Savi, A. S. de Paula, and D. C. Lagoudas, “Numerical investigation of an adaptive vibration absorber using shape memory alloys,” Journal of Intelligent Material Systems and Structures, Vol. 22, No. 1, pp. 67–80, Jan. 2011, https://doi.org/10.1177/1045389x10392612
-
R. A. Aguiar, M. A. Savi, and P. M. Pacheco, “Experimental investigation of vibration reduction using shape memory alloys,” Journal of Intelligent Material Systems and Structures, Vol. 24, No. 2, pp. 247–261, Jan. 2013, https://doi.org/10.1177/1045389x12461696
-
H. Huang and W.-S. Chang, “Application of pre-stressed SMA-based tuned mass damper to a timber floor system,” Engineering Structures, Vol. 167, pp. 143–150, Jul. 2018, https://doi.org/10.1016/j.engstruct.2018.04.011
-
J. Seo, Y. Kim, and J. Hu, “Pilot study for investigating the cyclic behavior of slit damper systems with recentering shape memory alloy (SMA) bending bars used for seismic restrainers,” Applied Sciences, Vol. 5, No. 3, pp. 187–208, Jul. 2015, https://doi.org/10.3390/app5030187
-
M. S. Alam, M. A. Youssef, and M. Nehdi, “Utilizing shape memory alloys to enhance the performance and safety of civil infrastructure: a review,” Canadian Journal of Civil Engineering, Vol. 34, No. 9, pp. 1075–1086, Sep. 2007, https://doi.org/10.1139/l07-038
-
S. Moradi and M. S. Alam, “Feasibility study of utilizing superelastic shape memory alloy plates in steel beam-column connections for improved seismic performance,” Journal of Intelligent Material Systems and Structures, Vol. 26, No. 4, pp. 463–475, Mar. 2015, https://doi.org/10.1177/1045389x14529032
-
J. Tan, J. Jiang, M. Liu, Q. Feng, P. Zhang, and S. Ho, “Implementation of shape memory alloy sponge as energy dissipating material on pounding tuned mass damper: An experimental investigation,” Applied Sciences, Vol. 9, No. 6, p. 1079, Mar. 2019, https://doi.org/10.3390/app9061079
-
Y. T. Wu, H. L. Hu, and C. Y. Lee, “Finite element analysis of an acoustic metamaterial plate incorporating tunable shape memory cantilever absorbers,” in Journal of Physics: Conference Series, Vol. 1509, No. 1, p. 012002, Apr. 2020, https://doi.org/10.1088/1742-6596/1509/1/012002
-
R. D. Blevins and R. Plunkett, “Formulas for natural frequency and mode shape,” Journal of Applied Mechanics, Vol. 47, No. 2, pp. 461–462, Jun. 1980, https://doi.org/10.1115/1.3153712
-
L. C. Brinson, “One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable,” Journal of Intelligent Material Systems and Structures, Vol. 4, No. 2, pp. 229–242, Apr. 1993, https://doi.org/10.1177/1045389x9300400213
-
N. Vaiana, S. Sessa, F. Marmo, and L. Rosati, “A class of uniaxial phenomenological models for simulating hysteretic phenomena in rate-independent mechanical systems and materials,” Nonlinear Dynamics, Vol. 93, No. 3, pp. 1647–1669, Aug. 2018, https://doi.org/10.1007/s11071-018-4282-2
-
N. Vaiana, S. Sessa, and L. Rosati, “A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena,” Mechanical Systems and Signal Processing, Vol. 146, p. 106984, Jan. 2021, https://doi.org/10.1016/j.ymssp.2020.106984
About this article
The financial support from the joint research program between National Taipei University of Technology and Shenchen University under Grant No. NTUT-SZU-108-10 is gratefully acknowledged. In addition, the support from National Natural Science Foundation of China under Grant No. 52005341 is also acknowledged.

