Research on ride comfort of vibratory rollers: Part-1 Study on the effect of different cab isolation mounts

1. Introduction

The soil compactor often works in factories and construction site, and its operation process includes a combined static and dynamic forces of all the vehicle and the drum to compress the asphalt, terrain, or other materials. The vibration excitations from the deformable terrain and the drum are thus transmitted the driver via the cab and the vehicle's isolation systems. Consequently, the isolation system of the cab is one of the most important indexes for the improvement of the vehicle's ride quality.

Basic studies of the interaction between the wheel and deformable terrain [1-4] and of interaction between the elastic/plastic ground and drum [5] showed that the response in the vibration process of the vehicle had been strongly affected by terrains. Almost the isolation mounts of the cab of vibratory rollers were equipped by the traditional rubber with its high-stiffness coefficient and low-damping coefficient of the rubber materials [5, 6]. Thus, the high-stiffness of the rubber helped suppress only noise and vibration in the high frequency region, on the contrary, the low-damping coefficient of the rubber could generate the vibration with its high-magnitudes to reduce the ride quality of the vehicle [6]. The effect of designed dynamic parameters of the rubber mounts of the cab on the ride quality had been evaluated [7]. An optimal design for the cab’s new rubber mounts of soil compactors was built via the finite element model, and the new rubber mount was then produced and tested for the vehicle’s cab [6]. The dynamic parameters of the rubber mounts of the cab had been also optimized for improving the ride quality [8]. The research results concluded that the vehicle’s ride quality was significantly improved. But, the study results also showed that the large-amplitude shock of the cab existed at low-frequency region in the direction of forwarding motion. This is one of the reasons causes tiredness of the driver while working, cracking surfaces of the cab and other problems. Thus, to solve this problem, the low damping coefficients of the cab’s rubber mounts (RM) needs to be improved.

The hydraulic mounts (HM) were investigated and applied on the cab isolations of industrial vehicle, construction equipment, and earth-moving machinery to reduce the vibrations from the vehicle frame transmitted the cab floor and improve the ride quality [9, 10]. A cab model of off-road soil compactors equipped with the HM was also studied under the random excitation of the rigid road surface in a low-frequency range [11, 12]. The results showed that the ride comfort was greatly improved by hydraulic mounts. Additionally, the hydro-pneumatic mounts (HPM) researched for agricultural tractors and dump trucks to enhance the ride comfort as well as reduce the energy [13, 14] were applied on the cab’s isolation mounts of the vibratory rollers for improving the moving quality of the vehicle [15, 16]. Researches indicated that the ride quality of the cab had been strongly increased. However, the analysis the effect of the dynamic parameters of both the HM and HPM to understand their characteristics on the vibration isolation has not been researched yet.

In this study, a dynamics model based on the actual vibratory rollers is built under the vibration excitations consisted by the drum/tires-deformable terrain contact in the condition of the vehicle traveling; and of an excitation of the drum 28 Hz in the condition of the vehicle working in an elastic/plastic ground. The characteristics of the RM, HM, and HPM on the vibratory roller ride comfort are then analyzed compared via the root-mean-square (RMS) of the acceleration responses of the vertical driver’s seat and cab’s pitch angle, respectively. The improvement of the ride quality and control of the cab shaking is this study aim.

2. The dynamics model for the vibratory roller

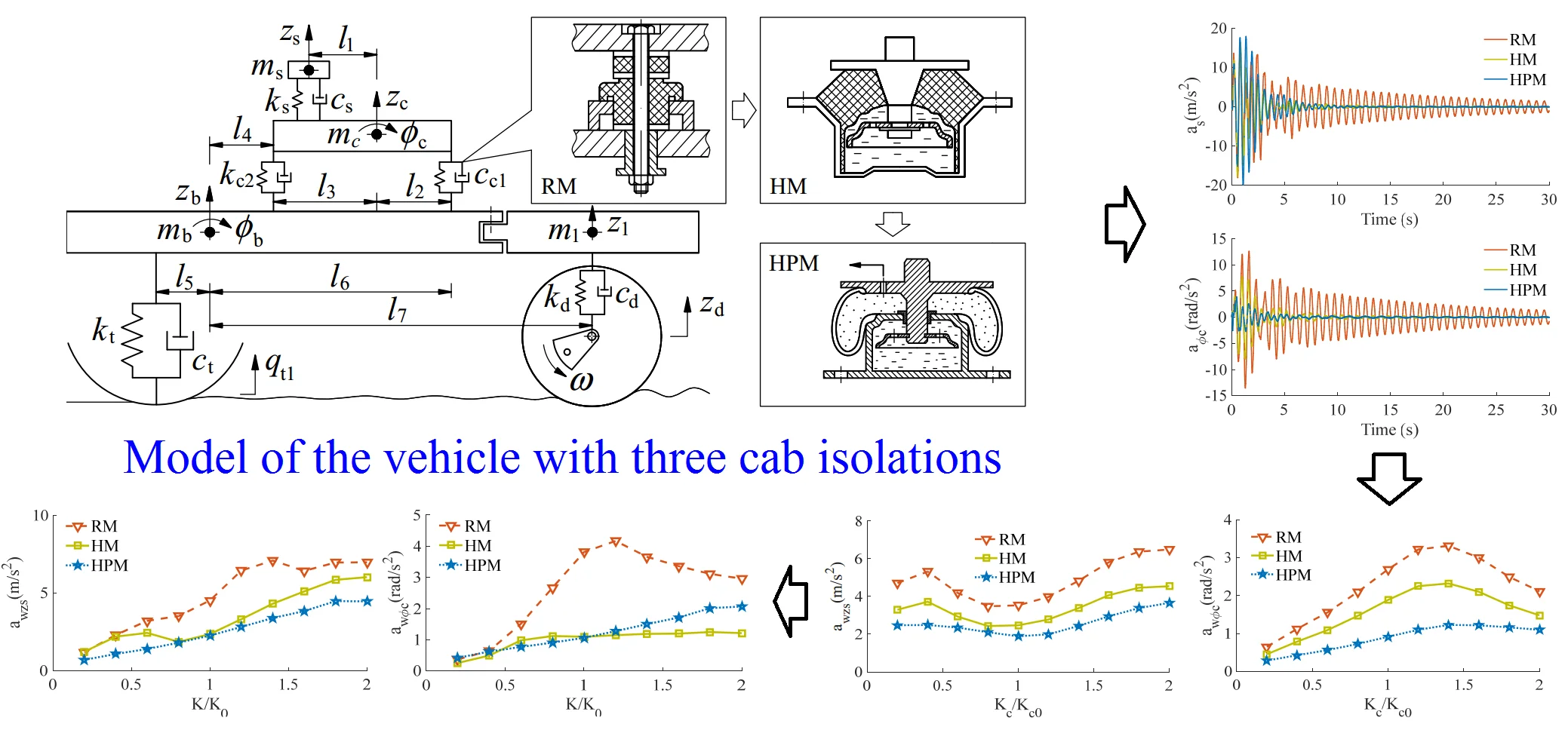
Vibratory roller has been mainly composed of our parts: vibratory steel drum, vibration excitation mechanism, vibration isolation system, and walking mechanism. The vibrator drum is not only a working wheel but also a walking wheel. It is one of the important parts of vibrating roller. Its weight accounts for about 80 % of the total vibration. The vibration damping system is composed of multiple shock absorbers which are used for vibration isolation and vibration reduction connection between vibration wheel and frame. The nonlinear dynamic model of vehicle is modeled as in Fig. 1, where, $z_b$, $z_1$, $z_c$, and $z_s$ are the vertical displacement of the rear frame, front frame, cab, and seat; $z_d$ is the vertical displacement of the flat section of the drum-ground contact surface; $m_b$, $m_1$, $m_c$, and $m_s$ are the weights of the rear frame, front frame, cab, and seat; $I_b$ and $I_c$ are the moment of inertia of the rear frame and the cab; $k_s$, $k_{c1}$, and $k_{c2}$ are the stiffness of the vibration isolators of the seat, front and rear cab, respectively; $c_s$, $c_{c1}$, and $c_{c2}$ are the damping of the vibration isolators of the seat, front and rear cab, respectively; $q_{t1}$ is excitation of the road roughness; ${\varphi }_c$ and ${\varphi }_b$ are the cab and rear frame's pitch angles; $l_1$, $l_2$, $l_3$, $l_4$, $l_5$, $l_6$, and $l_7$ are the geometric dimensions.

Fig. 1The nonlinear dynamics model of vibratory rollers with different cab isolations

Based on the model of the vibratory roller dynamics in Fig. 1, the different dynamic equations of the vehicle are listed as follows:

3. Modeling of Cab isolation systems

To evaluate the effect of the lumped parameters of the different isolation mounts of the cab including the RM, HM, and HPM, as plotted in Fig. 1, their mathematical models are then given in Fig. 2.

Fig. 2The model of the different cab isolations

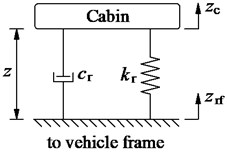
a) Rubber mount (RM)

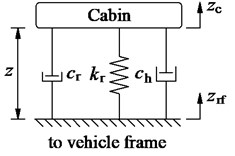
b) Hydraulic mount (HM)

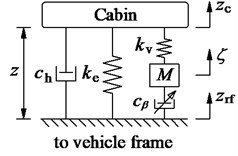
c) Hydro-pneumatic mount (HPM)

With the RM, as plotted in Fig. 1 and Fig. 2(a), it is made of rubber and metal and it can effectively isolate vibration by absorbing vibration energy. It is defined by a low damping coefficient $c_r$ and high stiffness $k_r$. The corresponding vertical dynamic forces of the front and rear RMs are given as follows:

With the HM, as plotted in Fig. 1 and Fig. 2(b), it includes a main rubber material and a damper with its damping coefficient $c_h$ used to isolator the vibration of the rear vehicle frame. Its mathematical equation is defined as follows [8, 9]:

With the HPM, as shown in both Fig. 1 and Fig. 2(c), it includes an airbag used together with a damper to isolator the vibrations. In the mathematical model of Fig. 2(c), herein, $k_v$ and $k_e$ are the coefficients of the HPM’s linear stiffness, $c_{\beta }$ is the main damping parameter of the pneumatic mount, and $c_h$ is the variable damping coefficient.

The corresponding vertical dynamic forces of the front and rear HPM are given as follows [5]:

where, $z_{ci}$ and $z_{rfi}$ in Eqs. (7-9) are the vertical displacements of suspension of cab and front and rear frames, $i=$ 1, 2.

4. Vibration sources of the terrain and drum

4.1. The interaction model between the elastic/plastic soil and drum

Based on the result of Adam and Kop [2, 3], the interaction model between the elastic/plastic soil and drum has been built in Fig. 3, and the properties of the elastic and plastic of the soil ground have been expressed by the factors $\epsilon$ and $\gamma$ as follows:

12

$\epsilon =\frac{k_{sp}}{k_{sp}+k_{se}},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\gamma =\frac{c_{se}}{k_{sp}},$

where, the parameters of $\epsilon$, $k_{se}$, $k_{sp}$, and $c_{se}$ are the compression ratio, elastic stiffness, compression stiffness, and compression damper.

Fig. 3The drum and elastic-plastic interaction

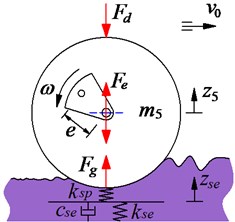
Based on the research results of Nguyen et al. [8-9], the interaction between the drum and deformable soil ground has been defined by three phases including loading phase, unloading phase, and drum-hope phase. The dynamic equations of three phases based on Refs. [7, 8] has been rewritten as follows:

13

$\left\{\begin{array}{l}\epsilon \gamma m_5{\stackrel{⃛}{z}}_5+m_5{\ddot{z}}_5=\epsilon \gamma {\dot{F}}_d+F_d-\epsilon c_{se}{\dot{z}}_5+\left(\epsilon -1\right)k_{sp}{z}_5\\ +\epsilon \gamma m{}_e{}^{\mathrm{}}\mathrm{}e{\omega }^3\mathrm{c}\mathrm{o}\mathrm{s}\omega t+m_{e}e{\omega }^2\mathrm{s}\mathrm{i}\mathrm{n}\omega t,\\ F_{dj}=k_{dj}[z_4-z_5+(-1{)}^j{b}_{j+3}({\theta }_4-{\theta }_5)]+c_{dj}[{\dot{z}}_4-{\dot{z}}_5+\left(-1{)}^j{b}_{j+3}\left({\dot{\theta }}_4-{\dot{\theta }}_5\right)\right],\end{array}\right.$

14

$m_5{\ddot{z}}_5=F_{dj}-c_{se}{\dot{z}}_5+m_{e}e{\omega }^2\mathrm{s}\mathrm{i}\mathrm{n}\omega t,$

15

$m_5{\ddot{z}}_5=F_{dj}+mg+m_{e}e{\omega }^2\mathrm{s}\mathrm{i}\mathrm{n}\omega t,j=\mathrm{1,2}.$

Eqs. (13-15) have been then used to calculate the motion of the drum $z_5$ and the excitation forces $F_d$.

5. Simulations and discussions

At present, the evaluation of vehicle vibration is mainly divided into two categories including subjective and objective evaluation. Due to the complexity of people’s subjective feelings, psychological and physiological characteristics need to be taken into account, and specialized personnel are needed to carry out the evaluation, so the subjective evaluation is subject to certain limitations. The objective evaluation method mainly considers the vibration isolation performance of the vehicle. The physical quantity of mechanical vibration (frequency, amplitude, acceleration, etc.) is taken as the evaluation index. Therefore, this objective evaluation is a widely used method. Vibration acceleration is the basic parameter for the ride comfort evaluation. According to the weighted root-mean-square (RMS) method of vibration acceleration recommended by ISO-2631, the RMS acceleration is calculated according to the following formula:

where, $T$ is the sampling time and $a\left(t\right)$ is the acceleration in the simulation porcess.

When vibratory rollers is moving or compressing on off-road grounds, the parameters of the stiffness and damping of the cab isolations, wheels, drum’s isolations not only affect the stability, durability and safety, but also impact the vehicle’s ride quality. Thus, the model of the vibratory roller is simulated to analyze the acceleration responses of the vertical driver's seat and the cab pitch angle with three cab isolations of the RM, HM, and HPM under different operation conditions of the vibratory roller.

5.1. Influence of the parameters of the cab isolations

To evaluate the performance of the cab isolations of the vibratory roller, based on the lumped parameters of the vibratory roller and cab isolation mounts in Tables 1 and 2, a single-drum vibratory roller working at the excitation frequency of the drum 28 Hz and 5 km/h on a hard soil ground is simulated. The simulation results of the acceleration responses of the vertical driver’s seat and pitching cab angle are plotted in Fig. 4.

The results show that the acceleration responses of the vertical driver and pitching cab angle with the HPM is the smallest while that of the RM is the biggest. Therefore, the vehicle’s ride comfort is strongly affected by the cab isolation system. To analyze the influence of the dynamic parameters of the isolations of the on the ride quality, the influence of the stiffness and damping parameters of the RM, HM, and HPM on the vibration of the vertical driver’s seat and the cab shaking will being researched.

Table 1The parameters of the vibratory rollers

Parameter	Value	Parameter	Value	Parameter	Value	Parameter	Value
$m_s$ / kg	85	$I_{cy}$ / kgm2	523	$l_4$ / m	0.136	$k_d$/ N m-1	3.9×106
$m_c$ / kg	891	$I_{by}$ / kgm2	1.2×104	$l_5$ / m	0.76	$k_t$ / N m-1	0.5×106
$m_b$ / kg	2822	$l_1$ / m	0.383	$l_6$ / m	0.9	$c_s$ / Ns m-1	1.2×102
$m_1$ / kg	4464	$l_2$ / m	0.1	$l_7$ / m	0.6	$c_d$ / Ns m-1	2.9×103
$m_d$ / kg	4378	$l_3$ / m	0.524	$k_s$ / N m-1	1.2×104	$c_t$ / Ns m-1	4.0×103

Table 2The parameters of the cab isolation mounts

Parameter	Value	Parameter	Value	Parameter	Value
$k_{r1}$ / Nm-1	9.1×105	$k_{v1}$/Nm-1	15.3×105	$c_{\beta 1}$ / Ns2m-2	12.4×103
$k_{r2}$ / Nm-1	1.2×105	$k_{v2}$/Nm-1	2.01×105	$c_{\beta 2}$ / Ns2m-2	10.7×103
$M_1$ / kg	98	$c_{r1}/$Nsm-1	218	$c_{h1}$ / Ns2m-2	20×103
$k_{e1}$ / Nm-1	9.1×105	$c_{r2}$/Nsm-1	29	$c_{h2}$ / Ns2m-2	4.5×103
$k_{e2}$ / Nm-1	1.2×105	$M_2$/kg	33	$\epsilon$	0.87

Table 3The parameters of the elastoplastic ground with its hard soil

Parameter	Value	Parameter	Value
$k_{sp}$ / N m-1	283×106	${\omega }_0$	2.14
$c_{se}$ / Ns m-1	37.1×103	$S\left(m_0\right)$ / m3 cyc-1	3782.5×10-6

Fig. 4The acceleration responses under a hard soil ground

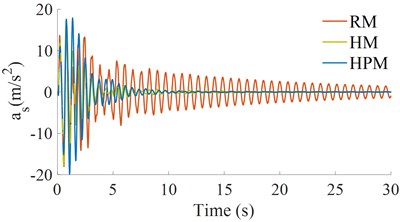
a) The vertical driver’s seat

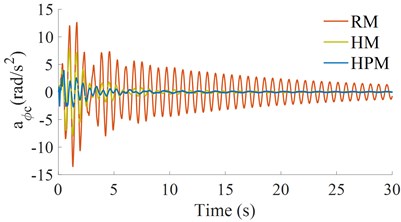
b) The pitching cab angle

5.1.1. Influence of the stiffness parameters

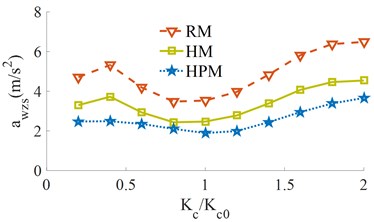
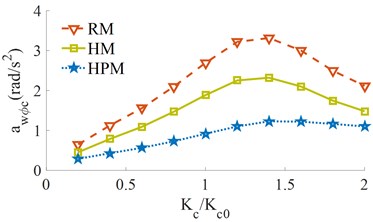
Under the same simulation condition of $v=$ 5 km/h of the vehicle and $f=$ 28 Hz of the drum on the hard soil ground, the different stiffness of the cab isolations $K_c=$ [0.2, 0.4, …, 2.0]×$K_{c0}$with the RM, HM, and HPM is selected to simulate the result. The effect of the different stiffness of the suspension system of the vehicle on the RMS acceleration responses of the vertical driver's seat ($a_{wz}$) and pitching cab angle ($a_{w\varphi c}$) is shown in Fig. 5.

Fig. 5The RMS acceleration responses under the different stiffness coefficients

a) The vertical driver’s seat

b) The pitching cab angle

The RMS acceleration response of the vertical driver’s seat ($a_{wz}$) in Fig. 5(a) shows that when the stiffness of the cab isolations is increased from 0.2×$K_{c0}$ to 0.8×$K_{c0}$, the $a_{wz}$ is slightly reduced. When the stiffness value is increased from 1.2×$K_{c0}$ to 2.0×$K_{c0}$, the $a_{wz}$ is strongly increased. With the stiffness values from 0.8×$K_{c0}$ to 1.2×$K_{c0}$, the $a_{wz}$ with all three RM, HM, and HPM is the smallest. This means that the vertical vibration of the driver’s seat is greatly improved. Besides, the RMS acceleration response of the pitching cab angle ($a_{w\varphi c}$) in Fig. 5(b) shows that when the stiffness of the cab isolations is increased from 0.2×$K_{c0}$ to 1.4×$K_{c0}$, the $a_{w\varphi c}$ is strongly increased. When the stiffness value is increased from 1.4×$K_{c0}$ to 2.0×$K_{c0}$, the $a_{w\varphi c}$ is significantly reduced. With the stiffness value of $K_c=$ 1.4×$K_{c0}$, the $a_{w\varphi c}$ is the bigest. Thus, the cab shaking is also the biggest. The comparison results between the RM, HM, and HPM in Fig. 5 show that both the $a_{wz}$ and $a_{w\varphi c}$ with the HPM is the smallest under the different stiffness coefficients. Therefore, the vehicle’s ride comfort is greatly improved by using the HPM. Additionally, a stiffness range of $K_c=$ [0.8 to 1.2]×$K_{c0}$ should be chosen to further improve the vehicle’s ride comfort and control the cab shaking.

5.1.2. Influence of the damping parameters

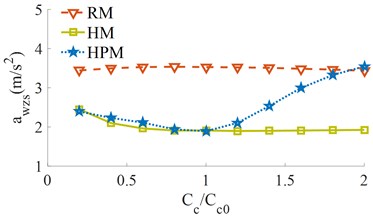
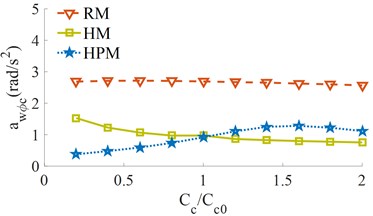
The different damping’s of $C_{c0}=$ [0.2, 0.4, …, 2]×$C_{c0}$ with three various isolations of the RM, HM, and HPM are simulated under the same simulation condition of Section 5.1.1. The simulation results are shown in Fig. 6.

The result shows that both the $a_{wz}$ and $a_{w\varphi c}$ with the RM is insignificanlty changed with the different damping coefficients of the RM. This is due to the $c_r$ value of the RM is very small. With the change of the $c_h$ values, both the $a_{wz}$ and $a_{w\varphi c}$ are significantly reduced when increasing the $c_h$ values, thus, the driver’s ride comfort and cab shaking is also improved by the increasing damping coefficient of the HM.

With the HPM, when the damping value is increased from 0.5×$C_{c0}$ to 1.0×$C_{c0}$, both the $a_{wz}$ and $a_{w\varphi c}$ are slightly reduced and smaller than that of the HM. Conversely, with the damping value of the HPM increased from 1.0×$C_{c0}$ to 2.0×$C_{c0}$, both the $a_{wz}$ and $a_{w\varphi c}$ are strongly increased and highter than that of the HM, thus, the vehicle’s ride comfort is greatly reduced. Based on the analysis results, the damping range of $C_c=$ [0.8 to 1.0]×$C_{c0}$ should be chosen to further improve the vehicle’s ride comfort and control the cab shaking with the HPM.

Fig. 6The RMS acceleration responses under the different damping coefficients

a) The vertical driver’s seat

b) The pitching cab angle

5.2. Influence of the parameters of the wheel and drum’s isolations

5.2.1. Influence of the stiffness parameters

Under the same simulation condition of $v=$ 5 km/h of the vehicle and $f=$ 28 Hz of the drum on the hard soil ground, the stiffness effect of the tires and drum isolations $K_{t,d}=$ [0.2, 0.4, …, 2.0]×$K_{t0,d0}$ on the $a_{wz}$ and $a_{w\varphi c}$is also obtained, as shown in Fig. 7.

Fig. 7The RMS acceleration responses under the different stiffness coefficients

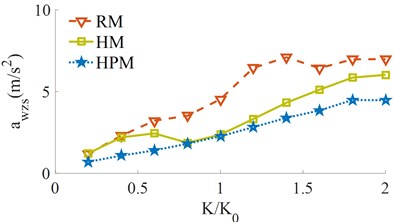
a) The vertical driver’s seat

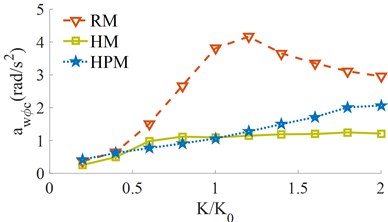
b) The pitching cab angle

The simulation results indicate that both the $a_{wz}$ and $a_{w\varphi c}$ with all the RM, HM, and HPM are quickly increased with the increase of the stiffness coefficient of both the tires and drum isolations from 0.2×$K_{t0,d0}$ to 2.0×$K_{t0,d0}$. Thus, the vertical driver’s ride comfort and cab shaking is greatly reduced. To improver the vehicle’s ride comfort, the stiffness value of the tires and drum isolations should be chosen by $K_{t,d}=$ [0.6 to 1.0]×$K_{t0,d0}$. Additionally, the performance of the HPM on the improvement of the vehicle’s ride comfort is insignificantly affected under the different stiffness values of the tires and drum isolations.

5.2.2. Influence of the damping parameters

Similarly, the effect of the different damping’s of the tires and drum isolations $C_{t,d}=$ [0.2, 0.4, …, 2.0]×$C_{t0,d0}$ on the $a_{wz}$ and $a_{w\varphi c}$ is simulated under the same condition of $v=$ 5 km/h of the vehicle and $f=$ 28 Hz of the drum on the hard soil ground. The simulation results are shown in Fig. 8.

The simulation results show that both the $a_{wz}$ and $a_{w\varphi c}$ with all the RM, HM, and HPM are significantly affected by the dampings of the tires and drum isolations. When the damping coefficients of the tires and drum isolations are increased from 0.2×$C_{t0,d0}$ to 2.0×$C_{t0,d0}$, both the $a_{wz}$ and $a_{w\varphi c}$ with both the RM and HM are reduced. However, the comparison result between the HM and HPM shows that with $C_{t,d}=$ [0.2 to 1.0]×$C_{t0,d0}$ and $C_{t,d}=$ [1.4 to 2.0]×$C_{t0,d0}$, the $a_{wz}$ of the HPM is higher than the HM, thus, the vehicle's ride comfort is reduced by using the HPM. To improve the vehicle’s ride comfort and cab shaking, the damping coefficients of the tires and drum isolations should be also chosen by $C_{t,d}=$ [1.0 to 1.2]×$C_{t0,d0}$.

Fig. 8The RMS acceleration responses under the different damping coefficients

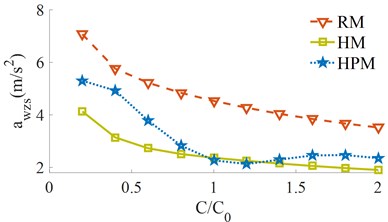
a) The vertical driver’s seat

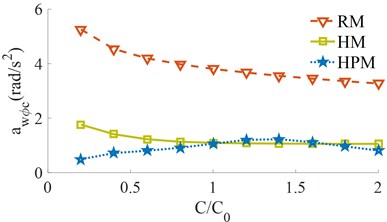
b) The pitching cab angle

6. Conclusions

Based on the simulation results of the effect of the vehicle and cab isolations’ parameters on the improvement of the ride comfort and cab shaking with three cab isolations of the RM, HM, and HPM in this paper, a conclusion can be drawn:

1) The different dynamic parameters of the vehicle and cab isolations have significant effect on the ride comfort of the vibratory roller.

2) Under the different simulation conditions of the dynamic parameters, the vehicle’s ride comfort and cab shaking with the HPM is better improved compared to both the RM and HM.

3) To optimize the vehicle’s ride comfort, the stiffness and damping parameters of the cab isolations, tires, and drum isolations should be designed in a range of $K_c=$ [0.8 to 1.2]×$K_{c0}$, $C_c=$ [0.8 to 1.0]×$C_{c0}$, $K_{t,d}=$ [0.6 to 1.0]×$K_{t0,d0}$, and $C_{t,d}=$ [1.0 to 1.2]×$C_{t0,d0}$.

4) To further improve the vehicle's ride comfort and control the cab shaking, the HPM with the damping coefficient of the hydraulic mount will be studied and controlled in Part-2.