Development and exploration of a mathematical model for transmission of monkey-pox disease in humans

Lasisi, N. O.; Akinwande, N. I.; Oguntolu, F. A.

doi:10.21595/mme.2019.21234

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 31 March 2020

Check for updates

Development and exploration of a mathematical model for transmission of monkey-pox disease in humans

N. O. Lasisi¹

N. I. Akinwande²

F. A. Oguntolu³

¹Department of Mathematics and Statistics, Federal Polytechnic, Kaura Namoda, Nigeria

^{2, 3}Department of Mathematics, Federal University of Technology, Minna, Nigeria

Corresponding Author:

N. O. Lasisi

Cite the article Download PDF

Downloads 1605

CrossRef Citations 22

0

Smart Citations

0

Citing PublicationsSupportingMentioningContrasting

View Citations

See how this article has been cited at scite.ai

scite shows how a scientific paper has been cited by providing the context of the citation, a classification describing whether it supports, mentions, or contrasts the cited claim, and a label indicating in which section the citation was made.

Abstract

In this paper, mathematical model of Monkey-Pox transmission is developed and investigated, using ordinary differential equation. We verified the feasible region of the model and showed the positivity of the solutions. We obtained the disease free equilibrium (DFE). We computed and analysed the effective basic reproduction number ( $R_{0}$ ) of the model.

Highlights

The study found the disease free equilibrium and effective reproduction number of the model equations
Epidemiological implication is that if the secondary cases of the monkey pox infection and human cases are on average less than one unit, then the disease will die out on the long run
The study incorporated exposure and vaccination class
The monkey pox will be eradicated among human population, provided R_h >1

1. Introduction

Monkey-pox is known as pathogens, affecting livestock animals and humans and belongs to the orthopox virus, which included small pox cause infection in humans and cow pox viruses [1]. The monkey pox causes lymph nodes to swell. The symptoms are fever, headache, muscle aches, backache, swollen lymph nodes, a feeling of discomfort and exhaustion. The virus is similar to small pox in human. The virus can spread both from animal to human and from human to human. The increased transmission risk associated with factors involving introduction of virus to the oral mucosa [2].

The incubation period range from 7 to 14 days. After 1 to 3 days of the appearance of fever, the patient develops raised bumps and the illness lasted for 2 to 4 weeks [5]. Thus, the reported case fatality ratio is range from 1 % to 10 % [3]. Currently, there are no vaccines for monkey pox, however, evidence showed that small pox vaccine reduced the risk of monkey pox among previously vaccinated persons in Africa [4, 5]. Centre for disease control and prevention also recommended that persons investigating monkey pox outbreaks and caring for infected individuals should vaccinated with small pox vaccine, to protect against the monkey pox. Individuals who have had close contact with persons confirmed to have monkey pox should be vaccinated up to 14 days after exposure were recommended [4].

Mathematical models have played a central role to capture the dynamics of different Disease transmission [6]. The aim of this paper is therefore to the development and exploration of a mathematical model for transmission of monkey-pox disease in humans. Therefore, there is non-numerous work on mathematical modelling of monkey pox transmission. This Paper extends the work of [7] by incorporating Vaccination class for migrants, Exposed classes for both human and non-human population.

2. Model formulation

We formulate a model for the spread of Monkey-pox in human and primates (Monkey) population with the total population size at time t given by $N_{h} (t)$ and $N_{p} (t)$ . The populations are further compartmentalized into epidemiological classes as shown in the model flow diagram in Fig. 1. The total human population is divided into five subgroups that is the Susceptible, $S_{h} (t)$ , the Vaccinated, $V_{h} (t)$ , the Exposed, $E_{h} (t)$ , the Infected, $I_{h} (t)$ , and the Recovery with permanent immunity, $R_{h} (t)$ . The total primates (Monkey) population model divides into the Susceptible, $S_{p} (t)$ , the Infected primates, $I_{p} (t)$ , the Exposed, $E_{p} (t)$ and the recovery with permanent immunity, $R_{p} (t)$ . As indicated in the compartmental diagram in Fig. 1, people enter Susceptible class through birth and immigration, ( $Λ_{h}$ ), where a proportion of vaccinated human immigrants ( $f$ ) enter to the vaccinated class and proportion of unvaccinated immigrants ( $1 - f$ ) enter to the susceptible class. We do not consider the immigration of infection person, because we assume that people who are coming from monkey-pox endemic zones have to be vaccinated. The susceptible individuals vaccinated at the rate $γ$ and loss the vaccination at the rate $ω$ . Susceptible human get contact from primate at rate $σ_{p_{1}}$ , $S_{h}$ are exposed to monkey-pox infection at the rate $σ_{h}$ and infected at the rate $β_{h}$ , with natural death $μ_{h}$ and die due to the infection at the rate $δ_{h}$ and recovery with permanent immunity at a rate $ρ_{h}$ . The Susceptible primates, $S_{p}$ class is generated from the daily recruitment of individuals through birth and immigration at the $Λ_{p}$ and natural death rate $μ_{p}$ . They become exposed to monkey-pox virus at the rate $σ_{p_{2}}$ and leave the class to infected class at the rate $β_{p}$ . Individuals primate infected die due to the infection at the rate $δ_{p}$ and recovery with the permanent immunity at the rate $ρ_{p}$ .

Fig. 1Schematic diagram of transmission of monkey-pox disease

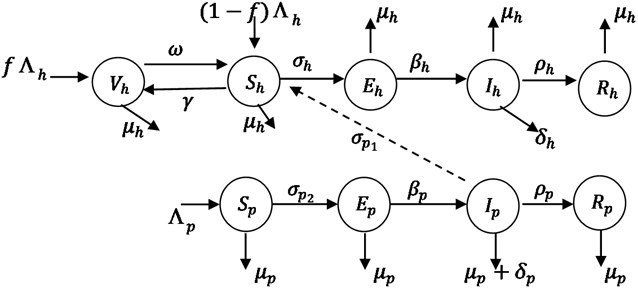
Base on the above assumptions and schematic diagram of Fig. 1, the model for transmission dynamics of Monkey-pox infection in human and primates (Monkey) is described by a system of Ordinary Differential Equations (ODEs) given below:

1

$\frac{d S_{h}}{d t} = (1 - f) Π_{h} + ω V_{h} - γ S_{h} - (\frac{σ_{p_{1}} (ε_{p} E_{p} + I_{p})}{N_{p}} + \frac{σ_{h} (ε_{h} E_{h} + I_{k})}{N_{h}}) S_{h} - μ_{h} S_{h},$

2

$\frac{d E_{h}}{d t} = (\frac{σ_{p_{1}} (ε_{p} E_{p} + I_{p})}{N_{p}} + \frac{σ_{h} (ε_{h} E_{h} + I_{k})}{N_{h}}) S_{h} - β_{h} E_{h} - μ_{h} E_{h},$

3

$\frac{d I_{h}}{d t} = β_{h} E_{h} - ρ_{h} I_{h} - μ_{h} I_{h} - δ_{h} I_{h},$

4

$\frac{d V_{h}}{d t} = f Π_{h} + γ S_{h} - ω V_{h} - μ_{h} V_{h},$

5

$\frac{d R_{h}}{d t} = ρ_{h} I_{h} - μ_{h} R_{h},$

6

$\frac{d S_{p}}{d t} = Π_{p} - (\frac{{σ_{p}}_{2} (ε_{p} E_{p} + I_{p})}{N_{p}}) S_{p} - μ_{p} S_{p},$

7

$\frac{d E_{p}}{d t} = (\frac{{σ_{p}}_{2} (ε_{p} E_{p} + I_{p})}{N_{p}}) S_{p} - β_{p} E_{p} - μ_{p} E_{p},$

8

$\frac{d I_{p}}{d t} = β_{p} E_{p} - ρ_{p} I_{p} - μ_{p} I_{p} - δ_{p} I_{p},$

9

$\frac{d R_{p}}{d t} = ρ_{p} I_{p} - μ_{p} R_{p},$

where:

10

$N_{h} {= S_{h} (t) + E_{h} (t) + I_{h} (t) + V_{h} (t) + R}_{h} (t),$

11

$N_{p} {= S_{p} (t) + E_{p} (t) + I_{p} (t) + R}_{p} (t) .$

The susceptible human host get infected from both the infected primate ( $I_{p}$ ) and infected human ( $I_{h}$ ) which is called force of infection from primates to human as well as human to human [7]. The term $σ_{p 1}$ is the product of the effective contact rate and probability of the human being get infected from the infected primates ( $I_{p}$ ) and $σ_{h}$ is the product of the effective contact and probability of the human get infected from the infected persons ( $I_{h}$ ). Similarly, the $S_{p}$ get infected from infected primate, where $σ_{p 2}$ is the product of the effective contact rate and probability of the primates (monkey) get infected per contact with an infected primate ( $I_{p}$ ) [7]. The modification parameter $ε_{h}$ account for the assumption that exposed human transmits at a rate lower than symptomatic humans. The modification parameter $ε_{p}$ account for the assumption that exposed non-human transmits at a rate lower than symptomatic non-humans. It is assumed here that mortality of monkeys due to being hunted by humans is negligible and can be safely ignored.

3. Analysis of the model equations

Theorem 1: (Invariant Region) the following biological feasible region of the model Eqs. (1)-(9) $Ω = {{S_{h}, E_{h}, I_{h}, V_{h}, R}_{h}$ , ${S_{p}, E_{p}, I_{p}, R}_{p}) \in R_{+}^{9}$ : ${{{S}_{h} (t) + E_{h} (t) + I_{h} (t) + V_{h} (t) + R}_{h} (t) \leq Λ_{h} / μ_{h}; S p t + E p t + I p t + R p (t) \leq Λ_{p} / μ_{p}}$ is positively invariant and attracting.

Proof; the addition of all the equations model in Eqs. (1)-(9) give:

$\frac{d N_{h}}{d t} = Λ_{h} - μ_{h} N_{h} - δ_{h} I_{h},$

$\frac{d N_{p}}{d t} = Λ_{p} - μ_{p} N_{p} - δ_{p} I_{p} .$

So that:

12

$\frac{d N_{h}}{d t} \leq Λ_{h} - μ_{h} N_{h}, \frac{d N_{p}}{d t} \leq Λ_{p} - μ_{p} N_{p} .$

It follows from [8], the Gronwall inequality, that:

13

$N_{h} (t) \leq N_{h} (0) e^{- μ_{h} (t)} + \frac{Λ_{h}}{μ_{h}} \{1 - e^{- μ_{h} (t)}\},$

$N_{p} (t) \leq N_{p} (0) e^{- μ_{p} (t)} + \frac{Λ_{p}}{μ_{p}} \{1 - e^{- μ_{p} (t)}\} .$

In particular, $N_{h} (t) \leq Λ_{h} / μ_{h}$ if $N_{h} (0) \leq Λ_{h} / μ_{h}$ and $N_{p} (t) \leq Λ_{p} / μ_{p}$ if $N_{p} (0) \leq Λ_{p} / μ_{p}$ . Thus, $Ω$ is positively invariant. Hence, it is sufficient to consider the model dynamics Eqs. (1)-(9) in $Ω$ , in this region, the model equations can be considered as been epidemiologically and mathematically well posed.

Theorem 2: (Positivity of the Solution for the Model). Let $t_{0} > 0$ and the initial conditions satisfied $S_{h} (0) > 0$ , $E_{h} (0) > 0$ , $I_{h} (0) > 0$ , $V_{h} (0) > 0$ , $R_{h} (0) > 0$ , $S_{p} (0) > 0$ , $E_{p} (0) >$ 0, $I_{p} (0) >$ 0, $R_{p} (0) > 0$ , then the solutions $S_{h} (t)$ , $E_{h} (t)$ , $I_{h} (t)$ , $V_{h} (t)$ , $R_{h} (t)$ , $S_{p} (t)$ , $E_{p} (t)$ , $I_{p} (t)$ , $R_{p} (t)$ , of the model Eqs. (1)-(9) are positive for all $t \geq 0$ .

Proof:

Proving that for all $t \in [0, t_{0}]$ , $S_{h} (t)$ , $E_{h} (t)$ , $I_{h} (t)$ , $V_{h} (t)$ , $R_{h} (t)$ , $S_{p} (t)$ , $E_{p} (t)$ , $I_{p} (t)$ , $R_{p} (t)$ will be positive in $R_{+}^{9}$ , Since all the parameters used in the system are positive. Thus, it is clear from Eq. (1) that:

$\frac{d S_{h}}{d t} = (1 - f) Λ_{h} + ω V - γ S_{h} - α_{h} S_{h} - μ_{h} S_{h} \geq - (γ + α_{h} + μ_{h} {) S}_{h} .$

So that:

14

$S_{h} (t) \geq {S_{h} (0) e}^{- (γ + α_{h} + μ_{h}) t - \int d t} \geq 0 o r S_{h} (t) \geq S_{h} (0) \exp \{- \int (γ + α_{h} + μ_{h}) d t\} .$

The similar approach can be used to show that $E_{h} (t) > 0$ , $I_{h} (t) > 0$ , $V_{h} (t) > 0$ , $R_{h} (t) > 0$ , $S_{p} (t) > 0$ , $E_{p} (t) >$ 0, $I_{p} (t) >$ 0, $R_{p} (t) > 0$ . Thus, for all $t \in [0, t_{0}]$ , $S_{h} (t)$ , $E_{h} (t)$ , $I_{h} (t)$ , $V_{h} (t)$ , $R_{h} (t)$ , $S_{p} (t)$ , $E_{p} (t)$ , $I_{p} (t)$ , $R_{p} (t)$ will be positive and remain in $R_{+}^{9}$ .

4. Existence of the equilibrium

At equilibrium state, we let:

15

$\frac{d S_{h}}{d t} = \frac{d E_{h}}{d t} = \frac{d I_{h}}{d t} = \frac{d V_{h}}{d t} = \frac{d R_{h}}{d t} = \frac{d S_{p}}{d t} = \frac{d E_{p}}{d t} = \frac{d I_{p}}{d t} = \frac{d R_{p}}{d t} = 0 .$

From Eq. (3), we have:

16

$E_{h} = \frac{(ρ_{h} + μ_{h} + δ_{h} {) I}_{h}}{β_{h}} .$

Substitute Eq. (16) into Eq. (2), we have:

17

$I_{h} (\frac{{(σ_{h} ε}_{h} (ρ_{h} + μ_{h} + δ_{h}) + σ_{h} β_{h}) S_{h}}{β_{h} N_{h}} - \frac{{(β}_{h} + μ_{h}) (ρ_{h} + μ_{h} + δ_{h})}{β_{h}}) = 0 .$

Equation (17) gives:

18

$I_{h} = 0 or (\frac{{(σ_{h} ε}_{h} (ρ_{h} + μ_{h} + δ_{h}) + σ_{h} β_{h}) S_{h}}{β_{h} N_{h}} - \frac{{(β}_{h} + μ_{h}) (ρ_{h} + μ_{h} + δ_{h})}{β_{h}}) = 0 .$

From Eq. (8), we have:

19

$E_{p} = \frac{(ρ_{p} + μ_{p} + δ_{p} {) I}_{p}}{β_{p}} .$

Substitute Eq. (19) into Eqs. (7), we have:

20

$I_{p} (\frac{(σ_{p 2} ε_{p} (ρ_{p} + μ_{p} + δ_{p}) + σ_{p} β_{p}) S_{p}}{{β_{p} N}_{p}} - \frac{(β_{p} + μ_{p}) (ρ_{p} + μ_{p} + δ_{p})}{β_{p}}) = 0 .$

Equation Eq. (20) gives:

21

$I_{p} = 0 or \frac{(σ_{p 2} ε_{p} (ρ_{p} + μ_{p} + δ_{p}) + σ_{p} β_{p}) S_{p}}{{β_{p} N}_{p}} - \frac{(β_{p} + μ_{p}) (ρ_{p} + μ_{p} + δ_{p})}{β_{p}} = 0 .$

Substitute $I_{h} = 0$ in Eq. (9) into Eq. (16) and Eq. (5), we have:

22

$E_{h} = R_{h} = 0 .$

Making $V_{h}$ subject of expression in Eq. (4) and Eq. (1), and equating them, we have:

23

$V_{h} = \frac{f Π_{h} + γ S_{h}}{(ω + μ_{h})} = \frac{γ S_{h} + α_{h} S_{h} + μ_{h} S_{h} - (1 - f) Π_{h}}{ω} .$

Implies:

$f Π_{h} + γ S_{h} ω = (γ S_{h} + α_{h} S_{h} + μ_{h} S_{h} - (1 - f) Π_{h}) (ω + μ_{h}) .$

Since $I_{h} = 0$ , implies $α_{h} = 0$ , then we have:

24

$S_{h} = \frac{f {ω Π}_{h} + [Π_{h} ω + Π_{h} μ_{h} - f Π_{h} ω - f Π_{h} μ_{h}]}{γ ω + γ μ_{h} + μ_{h} ω + {μ_{h}}^{2} - γ ω} .$

Reduced to:

25

$S_{h}^{0} = \frac{Π_{h} ω + Π_{h} μ_{h} - f Π_{h} μ_{h}}{γ μ_{h} + μ_{h} ω + {μ_{h}}^{2}} .$

If there is no vaccination, then $S_{h}^{0} = \frac{Π_{h} μ_{h}}{{μ_{h}}^{2}} = \frac{Π_{h}}{μ_{h}}$ as $ω = γ = f = 0$ .

Substitute Eq. (25) into Eq. (4), we have:

26

$V_{h}^{0} = \frac{f Π_{h} μ_{h} ω + f Π_{h} {μ_{h}}^{2} + γ Π_{h} ω + {γ Π_{h} μ}_{h}}{(γ μ_{h} + μ_{h} ω + {μ_{h}}^{2}) (ω + μ_{h})} .$

Substitute $I_{p} = 0$ in Eq. (21) into Eqs. (19) and (9), we have:

27

$E_{p} = R_{p} = 0 .$

From Eq. (6), we have:

28

$S_{p}^{0} = \frac{Π_{p}}{μ_{p}} .$

The disease free equilibrium (DFE) state is given as:

29

$E_{0} = {{S_{h}}^{*}, {E_{h}}^{*}, {V_{h}}^{*}, {I_{h}}^{*}, {R_{h}}^{*}, {S_{p}}^{*}, {E_{p}}^{*}, {I_{p}}^{*}, {R_{p}}^{*}}$

$= \{\frac{Π_{h} ω + Π_{h} μ_{h} - f Π_{h} μ_{h}}{γ μ_{h} + μ_{h} ω + {μ_{h}}^{2}}, 0, \frac{f Π_{h} μ_{h} ω + f Π_{h} {μ_{h}}^{2} + γ Π_{h} ω + {γ Π_{h} μ}_{h}}{(γ μ_{h} + μ_{h} ω + {μ_{h}}^{2}) (ω + μ_{h})}, 0, 0, \frac{Π_{p}}{μ_{p}}, 0, 0, 0\} .$

5. Effective basic reproduction number ( $R_{e}$ )

We applying next generation matrix operator to compute the effective basic reproduction number [9]. The largest Eigenvalue or spectral radius of $F V^{- 1}$ is the effective basic reproduction number of the model:

30

${F V}^{- 1} = [\frac{\partial F_{i} (E^{0})}{\partial x_{i}}] {[\frac{\partial V_{i} (E^{0})}{\partial x_{i}}]}^{- 1},$

where $F_{i}$ is the rate of appearance of new infection in compartment $i$ , $V_{i}$ is the transfer of infection from one compartment $i$ to another and $E^{0}$ is the Disease-Free Equilibrium.

Using this technique, we have spectral radius ( $ρ$ ) of the next generation matrix, $F V^{- 1}$ that is, $R_{0} = ρ (F V^{- 1})$ . Both $F$ and $V$ are obtained from the Jacobian matrix of the linearization of system Eqs. (1)-(9) disease free equilibrium. Therefore, the vector $F$ and $V$ representing inflow and outflow from compartments $E_{h}$ , $E_{p}$ , $I_{h}$ and $I_{P}$ are given by:

31

$f = (\begin{array}{l} f_{1} \\ f_{2} \\ f_{3} \\ f_{4} \end{array}) = (\begin{matrix} (\frac{σ_{p 1} (ε_{p} E_{p} + I_{p})}{N_{p}} + \frac{σ_{h} {(ε}_{h} E_{h} + I_{h})}{N_{h}}) S_{h} \\ β_{h} E_{h} \\ \frac{σ_{p 2} (ε_{p} E_{p} + I_{p}) S_{P}}{N_{p}} \\ β_{p} E_{p} \end{matrix}),$

32

$F = [\begin{array}{l} \frac{σ_{h} ε_{h} S_{h}^{0}}{N_{h}^{0}} & \frac{σ_{h} S_{h}^{0}}{N_{h}^{0}} & \frac{σ_{p_{1}} ε_{p} S_{h}^{0}}{N_{p}^{0}} & \frac{σ_{p_{1}} S_{h}^{0}}{N_{p}^{0}} \\ β_{h} & 0 & 0 & 0 \\ 0 & 0 & \frac{σ_{p_{2}} ε_{p} S_{p}^{0}}{N_{p}^{0}} & \frac{σ_{p_{2}} S_{p}^{0}}{N_{p}^{0}} \\ 0 & 0 & β_{p} & 0 \end{array}],$

33

$v = (\begin{matrix} v_{1} \\ v_{2} \\ v_{3} \\ v_{4} \end{matrix}) = [\begin{matrix} A_{1} E_{h} \\ A_{2} I_{h} \\ A_{3} E_{p} \\ A_{4} I_{p} \end{matrix}],$

where, $A_{1} = β_{h} + μ_{h}$ ; $A_{2} = ρ_{h} + μ_{h} + δ_{h}$ ; $A_{3} = β_{p} + μ_{p}$ ; $A_{4} = ρ_{p} + μ_{p} + δ_{p}$ and:

34

$V = (\begin{matrix} A_{1} \\ 0 \\ 0 \\ 0 \end{matrix} \begin{matrix} 0 \\ A_{2} \\ 0 \\ 0 \end{matrix} \begin{matrix} 0 \\ 0 \\ A_{3} \\ 0 \end{matrix} \begin{matrix} 0 \\ 0 \\ 0 \\ A_{4} \end{matrix}) .$

From Eqs. (34), we have:

35

$V^{- 1} = [\begin{matrix} 1 / A_{1} & 0 & 0 & 0 \\ 0 & 1 / A_{2} & 0 & 0 \\ 0 & 0 & 1 / A_{3} & 0 \\ 0 & 0 & 0 & 1 / A_{4} \end{matrix}] .$

At DFE, and since $N_{h} (t) \leq Π_{h} / μ_{h}$ and $N_{p} (t) \leq Π_{p} / μ_{p}$ we have:

36

$F = [\begin{matrix} \frac{σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h}} & \frac{σ_{h} μ_{h} S_{h}^{0}}{Π_{h}} & \frac{σ_{p_{1}} ε_{p} μ_{p} S_{h}^{0}}{Π_{p}} & \frac{σ_{p_{1}} μ_{p} S_{h}^{0}}{Π_{p}} \\ β_{h} & 0 & 0 & 0 \\ 0 & 0 & \frac{σ_{p_{2}} ε_{p} μ_{p} S_{p}^{0}}{Π_{p}} & \frac{σ_{p_{2}} μ_{p} S_{p}^{0}}{Π_{p}} \\ 0 & 0 & β_{p} & 0 \end{matrix}] .$

From Eq. (36), we have:

37

$F = [\begin{matrix} \frac{σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h}} & \frac{σ_{h} μ_{h} S_{h}^{0}}{Π_{h}} & \frac{σ_{p_{1}} ε_{p} μ_{p} S_{h}^{0}}{Π_{p}} & \frac{σ_{p_{1}} μ_{p} S_{h}^{0}}{Π_{p}} \\ β_{h} & 0 & 0 & 0 \\ 0 & 0 & σ_{p_{2}} ε_{p} & σ_{p_{2}} \\ 0 & 0 & β_{p} & 0 \end{matrix}],$

38

$F V^{- 1} = [\frac{\partial F_{i} (E^{0})}{\partial x_{j}}] {[\frac{\partial V_{i} (E^{0})}{\partial x_{j}}]}^{- 1} .$

Multiplying Eq. (37) and (35) together, we have:

39

$F V^{- 1} = [\begin{matrix} \frac{σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h}} & \frac{σ_{h} μ_{h} S_{h}^{0}}{Π_{h}} & \frac{σ_{p_{1}} ε_{p} μ_{p} S_{h}^{0}}{Π_{p}} & \frac{σ_{p_{1}} μ_{p} S_{h}^{0}}{Π_{p}} \\ β_{h} & 0 & 0 & 0 \\ 0 & 0 & σ_{p_{2}} ε_{p} & σ_{p_{2}} \\ 0 & 0 & β_{p} & 0 \end{matrix}] [\begin{matrix} \frac{1}{A_{1}} & 0 & 0 & 0 \\ 0 & \frac{1}{A_{2}} & 0 & 0 \\ 0 & 0 & \frac{1}{A_{3}} & 0 \\ 0 & 0 & 0 & \frac{1}{A_{4}} \end{matrix}] .$

Equation (39) implies:

40

$F V^{- 1} = [\begin{matrix} \frac{σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h} A_{1}} & \frac{σ_{h} μ_{h} S_{h}^{0}}{Π_{h} A_{2}} & \frac{σ_{p_{1}} ε_{p} μ_{p} S_{h}^{0}}{Π_{p} A_{3}} & \frac{σ_{p_{1}} μ_{p} S_{h}^{0}}{Π_{p} A_{4}} \\ \frac{β_{h}}{A_{1}} & 0 & 0 & 0 \\ 0 & 0 & \frac{σ_{p_{2}} ε_{p}}{A_{3}} & \frac{σ_{p_{2}}}{A_{4}} \\ 0 & 0 & \frac{β_{p}}{A_{3}} & 0 \end{matrix}] .$

The characteristics equation of Eq. (40), gives $|{F V}^{- 1} - λ I| = 0$ :

41

$[\begin{matrix} K_{1} S_{h}^{0} - λ & K_{2} S_{h}^{0} & K_{3} S_{h}^{0} & K_{4} S_{h}^{0} \\ K_{5} & - λ & 0 & 0 \\ 0 & 0 & K_{6} - λ & K_{7} \\ 0 & 0 & K_{8} & - λ \end{matrix}] = 0,$

where:

42

$K_{1} = \frac{σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h} A_{1}}, K_{2} = \frac{σ_{h} μ_{h}}{Π_{h} A_{2}}, K_{3} = \frac{σ_{p_{1}} ε_{p} μ_{p}}{Π_{p} A_{3}}, K_{4} = \frac{σ_{p_{1}} μ_{p}}{Π_{p} A_{4}},$

$K_{5} = \frac{β_{h}}{A_{1}}, K_{6} = \frac{σ_{p_{2}} ε_{p}}{A_{3}}, K_{7} = \frac{σ_{p_{2}}}{A_{4}}, K_{8} = \frac{β_{p}}{A_{3}} .$

Determinant of Eq. (41) gives:

43

$(λ^{2} - K_{6} λ - K_{7} K_{8}) = 0 or (λ^{2} - K_{1} S_{h}^{0} λ - K_{2} K_{5} S_{h}^{0}) = 0 .$

To solve Eq. (43) with completing the square method, we have:

44

$λ_{1} = \frac{K_{6} \pm \sqrt{K_{6}^{2} + 4 K_{7} K_{8}}}{2},$

$λ_{1} = \frac{\frac{σ_{p_{2}} ε_{p}}{(β_{p} + μ_{p})} \pm \sqrt{\frac{(σ_{p_{2}} ε_{p})^{2}}{(β_{p} + μ_{p})^{2}} + \frac{4 σ_{p_{2}} β_{p}}{(β_{p} + μ_{p}) (ρ_{p} + μ_{p} + δ_{p})}}}{2} .$

$λ_{1}$ is the spectral radius of $ρ (F V^{- 1})$ and the reproduction number is the largest eigenvalue from Eq. (44):

45

$R_{p} = \frac{\frac{σ_{p_{2}} ε_{p}}{(β_{p} + μ_{p})} + \sqrt{\frac{(σ_{p_{2}} ε_{p})^{2}}{(β_{p} + μ_{p})^{2}} + \frac{4 σ_{p_{2}} β_{p}}{(β_{p} + μ_{p}) (ρ_{p} + μ_{p} + δ_{p})}}}{2},$

$(λ^{2} - K_{1} S_{h}^{0} λ - K_{2} K_{5} S_{h}^{0}) = 0 .$

Implies:

46

$λ_{2} = \frac{K_{1} S_{h}^{0} \pm \sqrt{K_{1}^{2} S_{h}^{0^{2}} + 4 K_{2} K_{5} S_{h}^{0}}}{2} .$

47

$λ_{2} = \frac{\frac{σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h})} \pm \sqrt{\frac{{σ_{h}}^{2} {ε_{h}}^{2} {μ_{h}}^{2} S_{h}^{0^{2}}}{Π_{h}^{2} (β_{h} + μ_{h})^{2}} + \frac{4 σ_{h} μ_{h} β_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h}) (ρ_{h} + μ_{h} + δ_{h})}}}{2} .$

$λ_{2}$ is the spectral radius of $ρ (F V^{- 1})$ :

48

$R_{h} = \frac{\frac{σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h})} + \sqrt{\frac{{σ_{h}}^{2} {ε_{h}}^{2} {μ_{h}}^{2} S_{h}^{0^{2}}}{Π_{h}^{2} (β_{h} + μ_{h})^{2}} + \frac{4 σ_{h} μ_{h} β_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h}) (ρ_{h} + μ_{h} + δ_{h})}}}{2} .$

Then, we obtained effective basic reproduction number as Eqs. (48) and (45). There are two host populations and it was shown from the model flow diagram in Fig. 1 that the monkey transmits the infection to human host and human to human. Hence, the effective basic reproduction number can be represented as:

49

$R_{0} = R_{h} + R_{p},$

50

$R_{0} = \frac{(\begin{array}{l} \frac{σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h})} + \frac{σ_{p_{2}} ε_{p}}{(β_{p} + μ_{p})} \\ + \sqrt{\frac{{σ_{h}}^{2} {ε_{h}}^{2} {μ_{h}}^{2} S_{h}^{0^{2}}}{Π_{h}^{2} (β_{h} + μ_{h})^{2}} + \frac{4 σ_{h} μ_{h} β_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h}) (ρ_{h} + μ_{h} + δ_{h})}} \\ + \sqrt{\frac{(σ_{p_{2}} ε_{p})^{2}}{(β_{p} + μ_{p})^{2}} + \frac{4 σ_{p_{2}} β_{p}}{(β_{p} + μ_{p}) (ρ_{p} + μ_{p} + δ_{p})}} \end{array})}{2} .$

5.1. Analysis of effective basic reproduction number on $R_{p}$ and $R_{h}$

Form Eq. (45), we have:

$R_{p} = \frac{M_{1} + \sqrt{{M_{1}}^{2} + M_{2}}}{2},$

where:

51

$M_{1} = \frac{σ_{p_{2}} ε_{p}}{(β_{p} + μ_{p})}, M_{2} = \frac{4 σ_{p_{2}} β_{p}}{(β_{p} + μ_{p}) (ρ_{p} + μ_{p} + δ_{p})} .$

Since the disease will not be established in the population if the secondary cases on average is less than a unit ( $R_{p} \leq 1$ ), this implies:

52

$R_{p} = \frac{M_{1} + \sqrt{{M_{1}}^{2} + M_{2}}}{2} \leq 1,$

53

$M_{1} + \sqrt{{M_{1}}^{2} + M_{2}} \leq 2, R_{p} \leq 1 .$

From Eqs. (53), we have:

54

$M_{2} = 4 - 4 M_{1} .$

Implies:

55

$\frac{4 σ_{p_{2}} β_{p}}{(β_{p} + μ_{p}) (ρ_{p} + μ_{p} + δ_{p})} \leq \frac{4 (β_{p} + μ_{p}) - 4 σ_{p_{2}} ε_{p}}{(β_{p} + μ_{p})} .$

From Eqs. (55), we make the product of the effective contact rate and probability of the primates (monkey) get infected per contact with an infected primate as a subject, we have:

56

$σ_{p_{2}} \leq \frac{4 (β_{p} + μ_{p}) (ρ_{p} + μ_{p} + δ_{p})}{4 β_{p} + 4 ε_{p} (ρ_{p} + μ_{p} + δ_{p})}, R_{p} \leq 1,$

57

$σ_{p_{2}} \leq P_{p}, R_{p} \leq 1,$

Where:

58

$P_{p} = \frac{4 (β_{p} + μ_{p}) (ρ_{p} + μ_{p} + δ_{p})}{4 β_{p} + 4 ε_{p} (ρ_{p} + μ_{p} + δ_{p})} .$

Also, we make the infected at the rate $β_{p}$ as a subject:

$4 σ_{p_{2}} β_{p} - 4 β_{p} (ρ_{p} + μ_{p} + δ_{p}) \leq 4 μ_{p} (ρ_{p} + μ_{p} + δ_{p}) - 4 σ_{p_{2}} ε_{p} (ρ_{p} + μ_{p} + δ_{p}),$

59

$β_{p} \leq \frac{μ_{p} (ρ_{p} + μ_{p} + δ_{p}) - σ_{p_{2}} ε_{p} (ρ_{p} + μ_{p} + δ_{p})}{σ_{p_{2}} - (ρ_{p} + μ_{p} + δ_{p})}, R_{p} \leq 1,$

60

$β_{p} \leq L_{p}, R_{p} \leq 1 .$

Where:

61

$L_{p} = \frac{μ_{p} (ρ_{p} + μ_{p} + δ_{p}) - σ_{p_{2}} ε_{p} (ρ_{p} + μ_{p} + δ_{p})}{σ_{p_{2}} - (ρ_{p} + μ_{p} + δ_{p})} .$

In a similar case, since the disease will not be established in the population if the secondary case on average is less than a unit ( $R_{h} \leq 1$ ).

Form Eq. (48), we have:

62

$R_{h} = \frac{Z_{1} + \sqrt{{Z_{1}}^{2} + Z_{2}}}{2},$

where:

63

$Z_{1} = \frac{σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h})}, Z_{2} = \frac{4 σ_{h} μ_{h} β_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h}) (ρ_{h} + μ_{h} + δ_{h})},$

64

$R_{h} = \frac{Z_{1} + \sqrt{{Z_{1}}^{2} + Z_{2}}}{2} \leq 1,$

65

$Z_{1} + \sqrt{{Z_{1}}^{2} + Z_{2}} \leq 2, R_{h} \leq 1 .$

From Eqs. (65), we have:

66

$Z_{2} \leq 4 - 4 Z_{1} .$

Implies:

67

$\frac{4 σ_{h} μ_{h} β_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h}) (ρ_{h} + μ_{h} + δ_{h})} \leq \frac{4 Π_{h} (β_{h} + μ_{h}) - 4 σ_{h} ε_{h} μ_{h} S_{h}^{0}}{Π_{h} (β_{h} + μ_{h})} .$

From Eqs. (67), we make the product of the effective contact and probability of the human get infected from the infected persons as a subject, we have:

68

$σ_{h} \leq \frac{4 Π_{h} (β_{h} + μ_{h}) (ρ_{h} + μ_{h} + δ_{h})}{4 μ_{h} β_{h} S_{h}^{0} + 4 ε_{h} μ_{h} S_{h}^{0} (ρ_{h} + μ_{h} + δ_{h})}, R_{h} \leq 1,$

69

$σ_{h} \leq P_{h}, R_{h} \leq 1,$

where:

70

$P_{h} = \frac{4 Π_{h} (β_{h} + μ_{h}) (ρ_{h} + μ_{h} + δ_{h})}{4 μ_{h} β_{h} S_{h}^{0} + 4 ε_{h} μ_{h} S_{h}^{0} (ρ_{h} + μ_{h} + δ_{h})} .$

Also, we make the infected at the rate $β_{h}$ as a subject:

71

$β_{h} \leq \frac{Π_{h} μ_{h} (ρ_{h} + μ_{h} + δ_{h}) - σ_{h} ε_{h} μ_{h} S_{h}^{0} (ρ_{h} + μ_{h} + δ_{h})}{σ_{h} μ_{h} S_{h}^{0} - Π_{h} (ρ_{h} + μ_{h} + δ_{h})}, R_{h} \leq 1,$

72

$β_{h} \leq L_{h}, R_{h} \leq 1,$

where:

73

$L_{h} = \frac{Π_{h} μ_{h} (ρ_{h} + μ_{h} + δ_{h}) - σ_{h} ε_{h} μ_{h} S_{h}^{0} (ρ_{h} + μ_{h} + δ_{h})}{σ_{h} μ_{h} S_{h}^{0} - Π_{h} (ρ_{h} + μ_{h} + δ_{h})} .$

6. Conclusions

The Monkey pox will be eradicated since the term $P_{p}$ is greater than the product of the effective contact rate and probability of the primates (monkey) $σ_{p_{2}}$ getting infected and the term $L_{p}$ is greater than infected rate $β_{p}$ as shown in Eq. (60), provided $R_{p} \leq 1$ . However, since $σ_{p_{1}} = 0$ , it means that there is no transmission between primates and humans population at disease free equilibrium. Similarly, the monkey pox will be eradicated among human population, since the term $P_{h}$ is greater than $σ_{h}$ and $L_{h}$ is greater than $β_{h}$ as shown in Eq. (72), provided $R_{h} \leq 1$ . Epidemiological implication is that if the secondary cases of the monkey pox infection and human cases are on average less than one unit, then the disease will die out on the long run.

In this paper, we developed a mathematical model of monkey-pox transmission disease. We analysed the invariant region and shown that the dynamics of model Eqs. (1)-(9) is in the region $Ω$ , the model equations was considered as been epidemiologically and mathematically well posed. The positivity of the solutions for the model was showed which implies that the solutions were positive and remains in $R_{+}^{9}$ . The disease free equilibrium and effective basic reproduction number of the model were obtained. Analyses of effective basic reproduction number were done.

References

Essbauer S., Pfeffer M., Meyer H. Zoonotic poxviruses. Veterinary Microbiology, Vol. 140, Issues 3-4, 2010, p. 229-236.

Publisher
Kantele A., Chickering K., Vapalahti O., et al. Emerging diseases – the monkey pox epidemic in the Democratic Republic of the Congo. Clinical Microbiology and Infection, Vol. 22, Issue 8, 2016, p. 658-659.

Publisher
Rimoin A. W., Kisalu N., Kebela Ilungam B., et al. Endemic human monkey pox, Democratic Republic of Congo, 2001-2004. Emerging Infectious Diseases, Vol. 13, Issue 6, 2007, p. 934-936.

Publisher
Centres for Disease Control Morbidity and Mortality Weekly Report. Atlanta, Georgia (MMWR), Vol. 52, Issue 27, 2003, p. 642-646.

Search CrossRef
What You Should Know About Monkeypox. Fact Sheet. Centres for Disease Control and Prevention, 2003.

Search CrossRef
Lasisi N. O., Akinwande N. I., Olayiwola R. O., et al. Mathematical model for Ebola virus infection in human with effectiveness of drug usage. Journal of Applied Sciences and Environmental Management, Vol. 22, Issue 7, 2018, p. 1089-1095.

Publisher
Bhunu C. P., Mushayabase S. Modelling the transmission dynamics of pox-like infections. International Journal of Applied Mathematics, Vol. 41, Issue 1, 2011, p. 2-9.

Search CrossRef
Bauch C., Earn D. Transients and attractors in epidemics. Proceedings of the Royal Society of London Series A, Vol. 270, Issue 1, 2003, p. 1573-1578.

Publisher
Van den Driessche P., Watmough J. Reproduction numbers and sub threshold endemic equilibria for the compartmental models of disease transmission. Mathematical Biosciences, Vol. 180, Issue 1, 2002, p. 29-48.

Publisher

Cited by

Mathematical Methods in Medical and Biological Sciences

Yerra Shankar Rao

(2025)

The Scientific Basis of Mpox (Monkeypox)

Jan Rychtář | Dewey Taylor | Oyita Udiani

(2025)

Fractal-fractional mathematical modeling of monkeypox disease and analysis of its Ulam–Hyers stability

Tharmalingam Gunasekar | Shanmugam Manikandan | Salma Haque | Murgan Suba | Nabil Mlaiki

(2025)

An Atangana–Baleanu derivative-based fractal-fractional order model for the monkey pox virus: A case study of USA

Khadija Tul Kubra | Samra Gulshan | Rooh Ali

(2024)

Understanding the Impact of HIV on MPOX Transmission in an MSM Population: A Mathematical Modeling Study

(2024)

Stability analysis of a fractional-order monkeypox epidemic model with quarantine and hospitalization

Raqqasyi R. Musafir | Agus Suryanto | Isnani Darti | Trisilowati

(2024)

Understanding the impact of HIV on mpox transmission in the MSM population: A mathematical modeling study

(2024)

Modeling on cost-effectiveness of monkeypox disease control strategies with consideration of environmental transmission effects in the presence of vaccination

Temesgen D. Awoke | Semu M. Kassa | Yibeltal A. Terefe | Manalebish D. Asfaw

(2024)

EFFECTS OF PUBLIC AWARENESS AND VACCINATION IN MODELING THE DYNAMICS OF MONKEY-POX TRANSMISSION DISEASE IN NIGERIA

Nurudeen Oluwasola Lasisi | Mohammed Rashad Abdullahi | Fahad Suleiman

(2024)

Epidemiological modeling of monkeypox clades: a dual-strain SEIR approach with stability, bifurcation, and sensitivity analysis

Dounia Bentaleb | Zakaria Khatar | Saida Amine

(2024)

Optimizing control strategies for monkeypox through mathematical modeling

Mohamed Baroudi | Imane Smouni | Hicham Gourram | Abderrahim Labzai | Mohamed Belam

(2024)

Optimal control analysis of Monkeypox disease with the impact of environmental transmission

Ahmed Alshehri | Saif Ullah

(2023)

Modeling and optimal control of monkeypox with cost-effective strategies

Olumuyiwa James Peter | Chinwendu E. Madubueze | Mayowa M. Ojo | Festus Abiodun Oguntolu | Tawakalt Abosede Ayoola

(2023)

A study on a monkeypox transmission model within the scope of fractal–fractional derivative with power-law kernel

Newton I. Okposo | Emmanuel Addai | Joshua S. Apanapudor | J. F. Gómez-Aguilar

(2023)

Adaptive changes in sexual behavior in the high‐risk population in response to human monkeypox transmission in Canada can help control the outbreak: Insights from a two‐group, two‐route epidemic model

(2023)

An investigation on the Monkeypox virus dynamics in human and rodent populations for a deterministic mathematical model

Leonce Leandry | Eunice W. Mureithi

(2023)

Mathematical Modeling of The Transmission Dynamics of Monkeypox with the Impact of Quarantine and Public Enlightenment in Nigeria

Sefiu Onitilo | Abiodun Ajanı | Deborah Danıel | Ayobami Haruna

(2023)

Mathematical Modeling and backward bifurcation in monkeypox disease under real observed data

F.M. Allehiany | Mahmoud H. DarAssi | Irfan Ahmad | Muhammad Altaf Khan | Elsayed M. Tag-eldin

(2023)

The transmission dynamics of the monkeypox virus in the presence of environmental transmission

Chinwendu E. Madubueze | Isaac O. Onwubuya | Godwin N. Nkem | Z. Chazuka

(2022)

Voluntary vaccination may not stop monkeypox outbreak: A game-theoretic model

(2022)

Modeling the effect of distancing and wearing of face masks on transmission of Covid-19 infection dynamics

Nurudeen O. Lasisi | Kolawole A. Adeyemo

(2021)

Optimal control and effect of poor sanitation on modelling the acute diarrhea infection

N. O. Lasisi | N. I. Akinwande | S. Abdulrahaman

(2020)

About this article

Received

05 December 2019

Accepted

17 December 2019

Published

31 March 2020

DOI

https://doi.org/10.21595/mme.2019.21234

Keywords

effective basic reproduction number

disease free equilibrium

mathematical modelling

monkey pox disease

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 05 23

Life prediction method of rolling bearing based on CNN-LSTM-AM

Wanqing Huang, Yang Chen, Yongqi Chen, Tao Zhang

Research article

2023 06 29

An ED-PSO model updating algorithm for structure health monitoring of beam-like structures

Can Wang, Dayang Li, Panida Kaewniam, Jie Wang, Tareq Al Hababi

Research article

2022 10 16

Optimization and characteristic analysis of screw rotor of a twin-screw pump

Zhi Yong Tian, Yong Qiang Zhao, Zhe Hui Li, Shi Liu, Da Hai Wang

Research article

2022 06 13

Numerical simulations on VIV of a flexible cylinder under two degree-of-freedoms excitations

Di Deng, Weicai Peng

N. O. Lasisi, N. I. Akinwande, and F. A. Oguntolu, “Development and exploration of a mathematical model for transmission of monkey-pox disease in humans,” Mathematical Models in Engineering, Vol. 6, No. 1, pp. 23–33, Mar. 2020, https://doi.org/10.21595/mme.2019.21234

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/mme.2019.21234
UR  - https://doi.org/10.21595/mme.2019.21234
TI  - Development and exploration of a mathematical model for transmission of monkey-pox disease in humans
T2  - Mathematical Models in Engineering
AU  - Lasisi, N. O.
AU  - Akinwande, N. I.
AU  - Oguntolu, F. A.
PY  - 2020
DA  - 2020/03/31
PB  - JVE International Ltd.
SP  - 23-33
IS  - 1
VL  - 6
SN  - 2351-5279
SN  - 2424-4627
ER  - 

Copy Ris

Copied to clipboard!

@article{Lasisi_2020,
	doi = {10.21595/mme.2019.21234},
	url = {https://doi.org/10.21595/mme.2019.21234},
	year = 2020,
	month = {mar},
	publisher = {{JVE} International Ltd.},
	volume = {6},
	number = {1},
	pages = {23--33},
	author = {N. O. Lasisi and N. I. Akinwande and F. A. Oguntolu},
	title = {Development and exploration of a mathematical model for transmission of monkey-pox disease in humans},
	journal = {Mathematical Models in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]N. O. Lasisi, N. I. Akinwande, and F. A. Oguntolu, “Development and exploration of a mathematical model for transmission of monkey-pox disease in humans,” Mathematical Models in Engineering, vol. 6, no. 1, pp. 23–33, Mar. 2020, doi: 10.21595/mme.2019.21234.

Copy IEEE

Copied to clipboard!

Lasisi, N. O., N. I. Akinwande, and F. A. Oguntolu. “Development and Exploration of a Mathematical Model for Transmission of Monkey-Pox Disease in Humans.” Mathematical Models in Engineering 6, no. 1 (March 31, 2020): 23–33. https://doi.org/10.21595/mme.2019.21234.

Copy Chicago

Copied to clipboard!

Development and exploration of a mathematical model for transmission of monkey-pox disease in humans

Abstract

Highlights

1. Introduction

2. Model formulation

3. Analysis of the model equations

4. Existence of the equilibrium

5. Effective basic reproduction number (Re<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mrow><mi mathvariant="bold-italic">R</mi></mrow><mrow><mi mathvariant="bold-italic">e</mi></mrow></msub></math>)

6. Conclusions

References

Cited by

About this article

Related Articles

5. Effective basic reproduction number ( $R_{e}$ )