Investigation and optimization of the cable force of a combined highway and railway steel truss cable-stayed bridge in completion state

1. Introduction

With the development of steel strength and steel truss cable-stayed bridge construction technology, the steel truss cable-stayed bridge has aroused increasing attention in the field of long-span highway and rail dual-purpose cable-stayed bridges [1]. The distribution of the bridge’s internal forces in the completion state is the most obvious indicator of the design quality of a cable-stayed bridge [2]. Accordingly, it is critical to determine a set of cable forces which ensure a cable-stayed bridge satisfies reasonable completion state requirements [3].

There are numerous methods of optimizing the cable force of cable-stayed bridges in a reasonable completion state at home and abroad. The primary methods are the rigid support continuous beam method, zero displacement method, specified stress method, internal force balance method [4], bending energy minimum method [5], bending moment square and minimum method, influence matrix method [6]and BP neural network method [7]. Steel truss cable-stayed bridges are often very complex in structure and have thousands of discrete members. Thus, traditional research methods are no longer applicable for optimizing the cable force in a reasonable completion state. The existing methods of improving the cable force of steel truss cable-stayed bridges are rare and difficult to promote [8].

By summarizing the previous studies and taking the Baijusi Yangtze river bridge in Chongqing as the object of study, the reasonable cable force of a highway and rail dual-purpose steel cable-stayed bridge in the completion state is analyzed, and a method for quickly determining the reasonable cable force is determined.

The novelties of this paper are as follows: firstly, compared with the traditional methods, the rigid supported continuous beam method combined with the influence matrix method can take into consideration the influence of the horizontal component of the stay cable forces when determining the reasonable cable force. Secondly, in most cases, the cable force in the reasonable completion state is optimized by a single method. There are few cases where two or more methods are combined for cable force optimization analysis.

2. Project overview

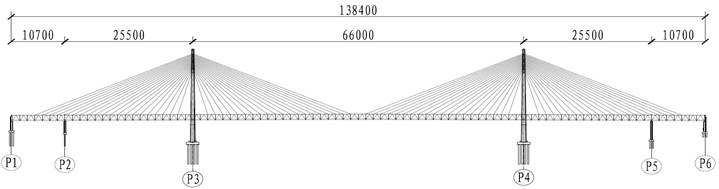
The bridge is a steel truss double-tower, double-cable plane highway and rail dual-purpose cable-stayed bridge. The ratio of the side to the middle span reaches 0.341. The span combination of the bridge is 107+255+660+255+107 = 1384 m and the ratio of the side to the middle span reaches 0.341. The geometry and main dimensions of the bridge are shown in Fig. 1.

Fig. 1Standard deck shape and dimensions (unit: cm)

3. Finite element model

In this study, the special Midas Civil 2015 finite element software for bridge structures is employed to build the computational model. The main beam trusses, beams, longitudinal beams and pylons are simulated by the spatial beam element. Taking shear deformation into account, the orthotropic bridge decks are simulated by the ribbed plate element, and the stay cables are simulated by tension-only trusses. The bridge is a cable-stayed bridge with a supporting system and a total of 15588 nodes and 35088 units. The full-bridge finite element model is shown in Fig. 2.

Fig. 2The finite element model of the Baijusi Yangtze river bridge

4. Rigid supported continuous beam method cable force improvement calculation

4.1. Bridge cable force output

The bridge has 160 cable-stayed cables in total. For the convenience of the following discussion, according to the structure’s principle of symmetry, it is assumed that the forces of the two cables in the transverse direction of the bridge are equal. The number of stay cables decreases from T20 to T1 from the shore side to the bridge tower and increases from M1 to M20 from the bridge tower to the middle of the span, as shown in Fig. 3.

The vertical reaction forces are calculated and analyzed, and the initial bridge cable forces are then determined. The results are shown in Table 1.

Fig. 3Labels of the cables

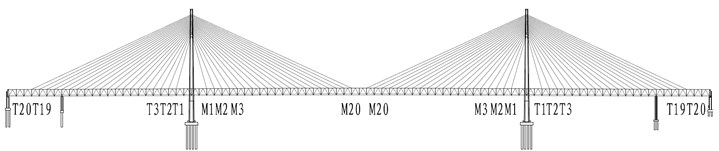
Table 1The initial bridge cable force table

Cable labels	Cable force (kN)	Cable labels	Cable force (kN)	Difference value	Percentage
T1	6426	M1	6428	–2	0
T2	4582	M2	4589	–7	0
T3	4281	M3	4344	–62	–1
T4	4295	M4	4297	–2	0
T5	4449	M5	4451	–1	0
T6	4683	M6	4688	–5	0
T7	4931	M7	4944	–12	0
T8	5164	M8	5198	–34	–1
T9	5349	M9	5430	–82	–2
T10	5613	M10	5605	8	0
T11	5952	M11	5851	101	2
T12	6387	M12	6185	203	3
T13	6974	M13	6439	535	8
T14	8275	M14	6679	1596	19
T15	8265	M15	6920	1345	16
T16	5160	M16	7168	–2008	–39
T17	9000	M17	7452	1548	17
T18	10024	M18	7909	2116	21
T19	10002	M19	8574	1428	14
T20	14151	M20	11575	2575	18

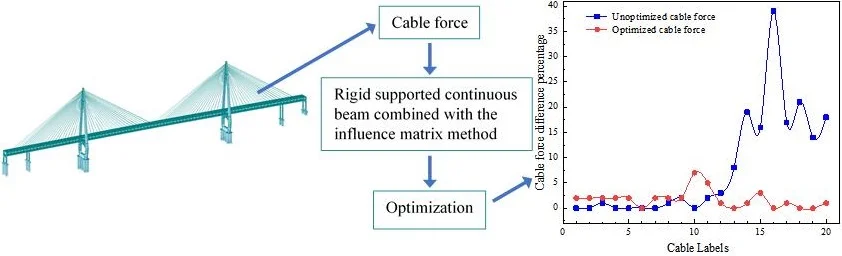
It can be concluded from the data in Table 1 that the cable-stayed cable force varies significantly around the auxiliary pier. The difference between the cable force of the symmetrical cable-stayed cables to the left and right of the bridge tower at the position of the auxiliary pier (T16) reaches 39 %. The cable force value shows a large jump, which is not consistent with the symmetry principle and the cable force distribution requirements in the reasonable completion state. It should be adjusted twice.

5. Comparative analysis

6. Conclusions

The finite element model of the Baijusi Yangtze River Bridge is established using Midas Civil 2015. Four methods are employed to determine the reasonable cable force of the bridge in the completion state, including the rigid support continuous beam method, bending energy minimum method, influence matrix method and BP neural network method combined with genetic algorithm. By comparing and analyzing the calculation results of each method and the complexity of the solution process, the following conclusions are drawn:

1) The force of the rigid support continuous beam method is clear and the alignment control of the main beam is good. However, this method does not consider the impact of the horizontal component of the cable-stayed cable. The displacement at the top of the bridge tower and the stress at the bottom of the bridge tower is too large. The cable force should be adjusted.

2) The minimum bending energy method considers the stress of the main beam and the bridge tower. The bending moment distribution of the main beam is uniform, but the main beam alignment control is poor, and it is difficult to modify the section bending stiffness for a highway and rail dual-purpose steel cable-stayed bridge with discrete members and variable cross-sections.

3) The influence matrix method is capable of controlling the multi-objective parameters by the single variable of the bridge cable force, and it is convenient for the realization of the objective function. The internal force, stress and deformation conditions of the bridge tower in the completion state are relatively moderate. This method can also simultaneously satisfy the requirements of the force and alignment of the tower beam. However, the control parameters should be calculated or have empirical values, and the solution process is complicated and cumbersome.

4) The BP neural network combined with genetic algorithm can quickly solve multiple sets of reasonable cable forces in the completion state, but it depends too heavily on the sample and the sampling process is complicated and time-consuming. The objective function directly determines the prediction accuracy and should be adjusted repeatedly.

5) By fully considering the stress of the main beam, and correcting the influence of the horizontal component force on the bridge tower and the unevenness of the cable force, the rigid support continuous beam combined with the influence matrix method is able to quickly determine the reasonable cable force of the steel truss cable-stayed bridge in the completion state. In comparison with the trial of the control parameters by the single influence matrix, the modification of the bending stiffness of the section by the bending minimum energy method, and the generation of the BP neural network and genetic algorithm samples, this method is simple and applicable, and can satisfy the actual needs of the project.