Magneto-thermal coupling analysis of the permanent magnet eddy current brake under intensive impact load

2.1. Mesh division of the eddy current brake

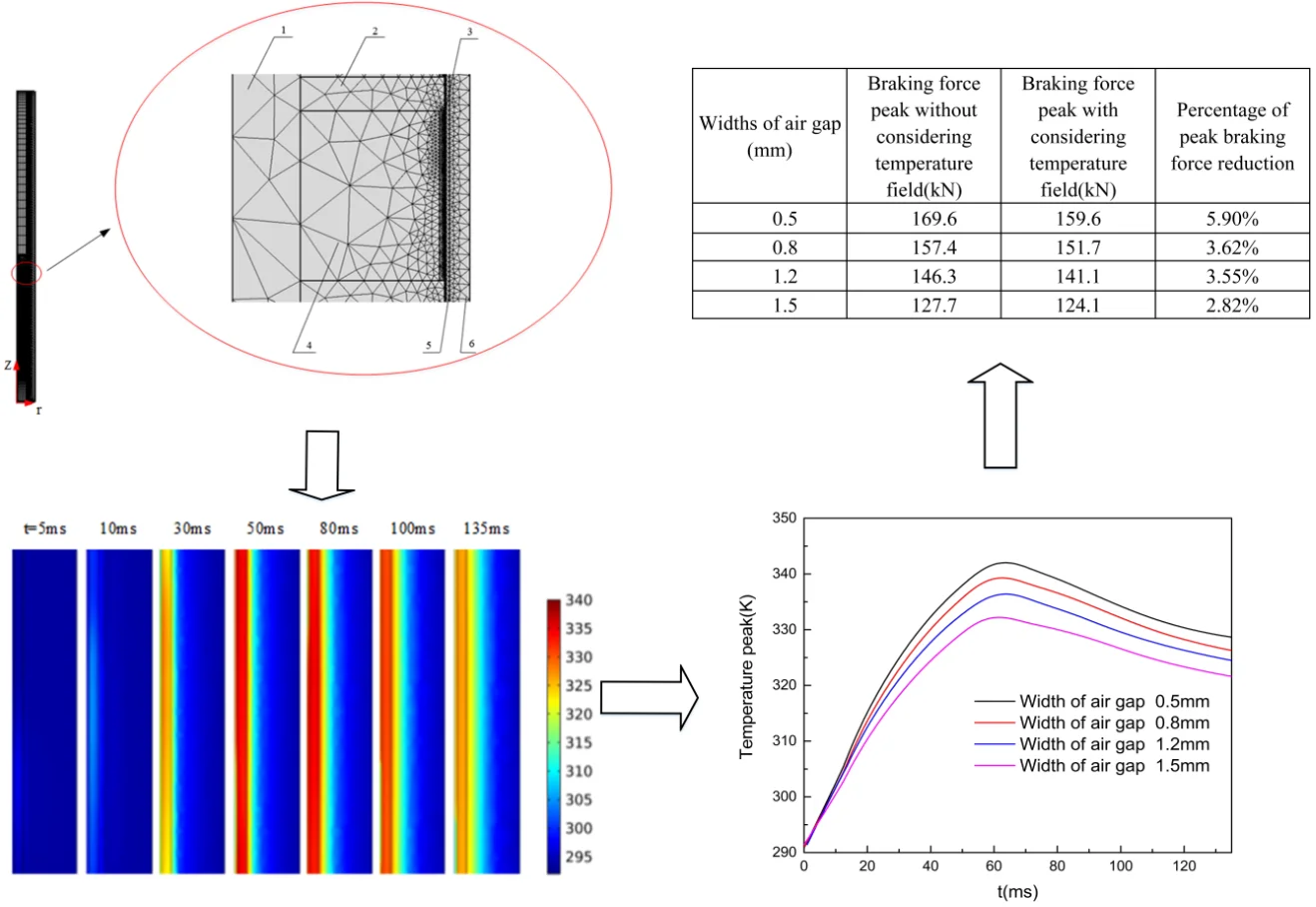
As Fig. 1 shows, the eddy current brake is divided by using the two-dimensional axisymmetric analysis method of AC/DC module in COMSOL. The eddy current brake includes primary: magnetic shoes, permanent magnets, the moving rod, secondary: the outer cylinder, the inner cylinder and the end cover. The primary moves under the impact load and the secondary is stationary when the eddy current brake is in operation. The relative motion between the primary and secondary will induce eddy currents on the inner cylinder. According to Lenz’s law, the magnetic flux generated by the eddy current will interact with the primary magnetic flux and then braking force is generated.

Fig. 1Structure diagram and mesh diagram of the eddy current brake

a)

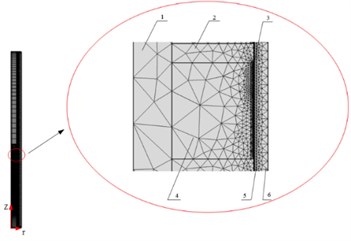
b) 1 – the moving rod; 2 – magnetic shoes; 3 – air gap; 4 – permanent magnets; 5 – the inner cylinder; 6 – the outer cylinder

2.2. Physical properties of the material

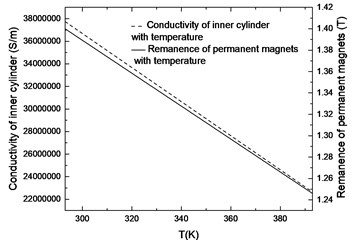
The magneto-thermal coupling has two forms: unidirectional coupling and bidirectional coupling. Unidirectional coupling makes the results of electromagnetic field analysis the initial conditions for thermal analysis. Thermal analysis does not affect the results of magnetic field analysis. Bidirectional coupling analysis is based on the data exchange of magnetic field and temperature field. When calculating in this way, the temperature field will affect the calculation of the magnetic field by affecting the magnetic properties of the material. In the bidirectional coupling model of this paper, the effects of temperature on the remanence of permanent magnets and the conductivity of the inner cylinder are considered.

(1) The effects of temperature on the remanence of permanent magnets.

In the permanent magnet eddy current brake, the strength of the magnetic field provided by the permanent magnets plays a decisive role in the magnitude of the braking force.

The permanent magnet used in this simulation is M-type sintered NdFeB. According to GB/T 13560, the relationship between remanence and temperature of NdFeB is shown in Fig. 2. Remanence is input to the simulation model in the form of a fitting function as follows:

(2) The effects of temperature on the conductivity of the inner cylinder

The inner cylinder is the carrier that generates eddy currents. When the temperature rises, the conductivity of the inner cylinder decreases. This will directly lead to a decrease in the braking force. Conductivity is also input to the simulation model in the form of a fitting function as follows:

Fig. 2Curve of inner cylinder conductivity and permanent magnet remanence with temperature

2.3. Temperature field physical model of eddy current brake

The three-dimensional heat transfer differential equation of temperature field is established according to the first law of thermodynamics and Fourier’s law:

where $\lambda$, $c$, $\rho$, $\tau$ and $q$ are the brake’s thermal conductivity, specific heat capacity, density time and, heat flow per unit time and volume, respectively.

During the temperature transmission of the linear eddy current brake, only heat conduction and convection are considered and the influence of radiation is ignored due to the limited temperature rise. The specific transmission process is shown in Fig. 3.

The convective of the inner cylinder to the air gap and the outer cylinder to the outside air is represented by the third type of boundary condition of the temperature field.

The inner and outer boundary condition are:

where $T_i$, $T_o$, $T_{airgap}$, and $T_{externalair}$ are the temperature of the inner cylinder, the outer cylinder, the air gap and the external air, respectively. $h_1$, $h_2$ are convective heat transfer coefficient of inner and outer boundary.

According to experimental research, the following formula can be used to express the convective heat transfer coefficient [11]:

where subscript $m$ means that the qualitative temperature is the membrane temperature. The membrane temperature $T_m$ is calculated as follows:

where $T_{air}$ and $T_{sur}$ are the temperature of air and surface, respectively.

$Gr$ and $Pr$ are the Grachev and Prandtl numbers. According to the literature, the coefficient $B=$ 0, $C=$ 0.53, and the index $n=$ 0.25:

The thermal conductivity ${\lambda }_m$, viscosity ${\nu }_m$, and expansion coefficient ${\beta }_m$ of air are defined as a function of temperature. The relationship between the convective heat transfer coefficient and temperature is shown in Fig. 4.

Fig. 3The route of temperature transfer

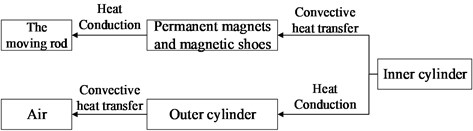
Fig. 4Curve of convective heat transfer coefficient with temperature

3.1. Temperature distribution of the eddy current brake in working process

It can be seen from Fig. 7 and Fig. 8 that the heat source is mainly generated in the inner cylinder and diffuses from the inner cylinder to both sides. The temperature on the inner cylinder is higher during the 50-80 ms period and the temperature peak reaches 340 K. After that, the temperature gradually expands to the outer cylinder region and the air gap layer. Due to the presence of the air gap layer, the temperature is not excessively transmitted to the permanent magnet region and the temperature rise of permanent magnets is not large.

Fig. 7Contour of temperature distribution over time

Fig. 8Curves of maximum temperature over time

3.2. Effect of temperature field on magnetic field

By comparing two pictures in Fig. 9, it is found that there is a difference in the calculation results between the simulation models with and without considering the temperature field. The braking force is smaller when the temperature field is taken into account. Table 1 lists the percentage of peak braking force reduction with different widths of air gap.

Fig. 9Braking force characteristics with widths of air gap uncoupled a) and coupled b) temperature field

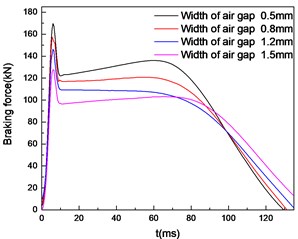
a)

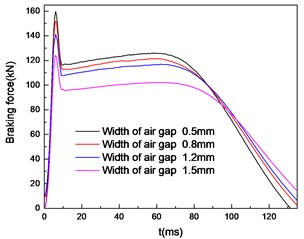
b)

Fig. 10Temperature peak of the brake with widths of air gap

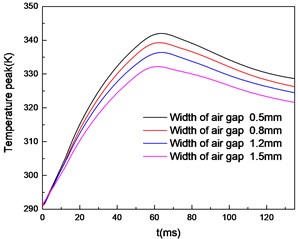
It can be found that the smaller the air gap width is, the greater the percentage of braking force reduction caused by temperature field is. This is because when the width of air gap decreases, the temperature increases as Fig. 10 shows. The weakening effect of temperature on braking force increases. So it is necessary to pay attention to heat dissipation while ensuring the magnitude of the braking force. This can avoid excessive influence on the braking performance of the brake.