Computing eigenpair derivatives of asymmetric damped system by generalized inverse

1. Introduction

In the past decades, damped system has become a topic of great interest to researchers because it arises frequently in many areas such as applied mechanics, electrical oscillation, vibro-acoustics, fluid dynamics, signal processing and so on. In this paper, we consider the equation of damped system with the following form [1]:

where the matrices $\mathbf{M}$, $\mathbf{C}$ and $\mathbf{K}$ are asymmetric and damping is non-proportional.

Studies on the sensitivity analysis of damped system have widely used in damage detection [2], system identification [3], carbon nanotube vibration [4], model updating [5, 6] and many other disciplines. The fundamental objective of sensitivity analysis is to compute the derivatives of eigenvalues and eigenvectors. Research on this topic has received much attention and many different algorithms [7-18] have been developed in a recent treatise. Most of the existing algorithms can be divided into two categories. The first category is to convert the damp system to undamped system by using linearization [7-9]. The second category is to differentiate Eq. (1) and compute the derivatives of eigenvectors directly [10-18]. Although there are various algorithms for damped system, most of existing approaches are based on the assumption that the eigenvalues are simple or semisimple with separated derivatives. In order to fill this gap, Qian et al. [19] relaxed the restriction that the repeated eigenvalues must have well separated derivatives and presented a new algorithm for computing eigensensitivity of damped system by utilizing the method of [20]. By using generalized inverses, Wang and Dai [21] introduced a method for computing the first-order derivatives of eigenvalues and eigenvectors for symmetric damped system.

Different from symmetric damped system, eigenvalues of an asymmetric damped system have different right and left eigenvectors. Therefore, the eigenvectors may be not unique by one normalization. By adopting an additional normalization to guarantee the uniqueness of the eigenvectors, we extend the method of [21] to asymmetric damped system in this paper. we derive the first-order derivatives of right and left eigenvectors regardless of whether the eigenvalues have multiple derivatives.

The structure of this paper is divided into five parts. We begin in Section 2 with a brief description of algorithm for eigenvalue derivatives, and Section 3 gives a comprehensive discussion on the derivations of the eigenvector in two cases according to whether the derivatives of the eigenvalue have multiple roots. A numerical example is presented to illustrate effectiveness of the proposed algorithm in Section 4. Section 5 concludes the paper with some final remarks.

2. Calculation of eigenvalues derivatives

We consider the damped system with parameters $p$. Suppose that ${\lambda }_i\left(p\right)$ is the eigenvalue and $u_{Ri}\left(p\right)$, $U_{Li}\left(p\right)$ are the corresponding right and left eigenvectors respectively, i.e.:

where $\mathbf{M}\left(p\right)$, $\mathbf{C}\left(p\right)$ and $\mathbf{K}\left(p\right)\in {\mathbf{C}}^{n\times n}$ are asymmetric analytic matrices and $\mathbf{M}\left(p\right)$ is nonsingular in this paper.

We consider the algorithm for eigenpair derivatives of Eq. (2) with multiple eigenvalue. For this reason, we suppose that ${\lambda }_0$ is the semisimple eigenvalue with multiplicity $r>1$ at $p_0$ and the column vectors of ${\mathrm{\Phi }}_R$, ${\mathrm{\Phi }}_L\in C_r^{n\times r}$ are the right and left eigenvectors respectively. From lemma 3 in Ref. [22], ${\mathrm{\Phi }}_L^T(2{\lambda }_0\mathbf{M}+\mathbf{C}){\mathrm{\Phi }}_R$ is non-singular. Without loss of generality, let ${\mathrm{\Phi }}_L$, ${\mathrm{\Phi }}_R$ satisfy:

Suppose $\mathrm{\Lambda }\left(p\right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\lambda }_1\right(p),\cdots ,{\lambda }_r(p\left)\right)$ and the eigenvector subsets:

are the eigenvalues functions and corresponding eigenvectors functions when $p$ varies at the neighborhood of $p_0$. Then:

where ${\mathbf{U}}_R\left(p\right)$, ${\mathbf{U}}_L\left(p\right)$ satisfy:

It is well known that the eigenvectors given by Eqs. (4), (5) and (6) are nonunique to the extent of a non-zero constant, and another normalized condition should imposed to result in unique eigenvectors and thereafter, for one to solve the corresponding eigenvectors derivatives. Because the mass matrix is not positive definite, the conventional mass normalization is not used. In this paper, the normalizing condition in Ref. [15] is adopted. Suppose:

The normalizing condition of ${\mathbf{u}}_{Ri}\left(p\right)\mathrm{}(i=1,\cdots ,r)$ is:

Because the linear combinations of eigenvectors corresponding to eigenvalues ${\lambda }_0$ are also eigenvectors of ${\lambda }_0$, we can express ${\mathrm{\Phi }}_R$, ${\mathrm{\Phi }}_L$ by the differentiable eigenvector subset ${\mathbf{U}}_R\left(p_0\right)$, ${\mathbf{U}}_L\left(p_0\right)$ in the following manner:

For the sake of simplify notation, $p_0$ is omitted for variables evaluated at $p=p_0$. Using Eq. (6) at $p=p_0$, we have:

Then:

i.e., ${\mathrm{\Gamma }}_R$ is the inverse of ${\mathrm{\Gamma }}_L^T$.

In order to compute $\mathrm{\Lambda }\mathrm{\text{'}}$ and ${\mathrm{\Gamma }}_R$, let $\mathbf{W}={\lambda }_0^2\mathbf{M}+{\lambda }_0\mathbf{C}+\mathbf{K}$, $\mathbf{W}\mathrm{\text{'}}={\lambda }_0^2\mathbf{M}\mathrm{\text{'}}+{\lambda }_0\mathbf{C}\mathrm{\text{'}}+\mathbf{K}\mathrm{\text{'}}$, where $(\cdot )\mathrm{\text{'}}$ denotes the derivative of $(\cdot )$. Differentiating both sides of Eqs. (2) and (3) with respect to $p$ and letting $p\to p_0$, one has:

where ${\mathbf{F}}_1=-(2{\lambda }_0\mathbf{M}+\mathbf{C}){\mathbf{U}}_R\mathrm{\Lambda }\mathrm{\text{'}}-\mathbf{W}\mathrm{\text{'}}{\mathbf{U}}_R\text{,}$${\mathbf{H}}_1=-\mathrm{\Lambda }\mathrm{\text{'}}{\mathbf{U}}_L^T(2{\lambda }_0\mathbf{M}+\mathbf{C})-{\mathbf{U}}_L^T\mathbf{W}\mathrm{\text{'}}\text{.}$ Premultiplying each side of Eq. (11) by ${\mathbf{U}}_L^T$ one obtains:

Substituting Eq. (9) into Eq. (13), we have:

where $\mathbf{D}=-{\mathrm{\Phi }}_L^T\mathbf{W}\mathrm{\text{'}}{\mathrm{\Phi }}_R.$ Eq. (14) shows that diagonal elements of matrix $\mathrm{\Lambda }\mathrm{\text{'}}$ are $n$ eigenvalues of $\mathbf{D}$ and matrix ${\mathrm{\Gamma }}_R$ are corresponding right eigenvectors matrix. Hence, solving eigenproblem $\mathbf{D}{\mathrm{\Gamma }}_R={\mathrm{\Gamma }}_R\mathrm{\Lambda }\mathrm{\text{'}}$ yields eigenvalues derivative $\mathrm{\Lambda }\mathrm{\text{'}}$ and matrix ${\mathrm{\Gamma }}_R$.

3. Calculation of eigenvectors derivatives

In this section, we will present a comprehensive discussion on the derivations of the eigenvectors according to whether the derivatives of the eigenvalues have multiple roots.

Case 1. The eigenvalues of Eq. (14) are distinct $({\lambda \mathrm{\text{'}}}_j\ne {\lambda \mathrm{\text{'}}}_{\left(k\right)},j\ne k,j,k=1,\cdots ,r)$. In this case, by solving Eq. (14) one can obtain the eigenvalue derivative $\mathrm{\Lambda }\mathrm{\text{'}}$ and the corresponding eigenvector matrix ${\mathrm{\Gamma }}_R$ uniquely up to scalar multipliers, and then ${\mathbf{U}}_R$ are determined by the relation ${\mathbf{U}}_R={\mathrm{\Phi }}_R{\mathrm{\Gamma }}_R$ and normalizing condition Eq. (7). In order to obtain ${\mathbf{U}}_{R\mathrm{\text{'}}}\text{,}$ we introduce the generalized inverse matrix $\mathbf{G}$ of matrix $\mathbf{W}$, i.e. $\mathbf{G}$ satisfies $\mathbf{W}\mathbf{G}\mathbf{W}=\mathbf{W}$. Then $\mathbf{G}{\mathbf{F}}_1$ will be a particular solution of Eq. (11) and the general solution of Eq. (11) can be expressed as:

where ${\mathbf{a}}_1$ is a $r\times r$ constant matrix. Let $\mathbf{H}=2{\lambda }_0\mathbf{M}+\mathbf{C}$, $\mathbf{H}\mathrm{\text{'}}=2{\lambda }_0\mathbf{M}\mathrm{\text{'}}+\mathbf{C}\mathrm{\text{'}}$, we will get another particular solution ${\mathbf{U}}_R^{\left(1\right)}$ of Eq. (11) by taking ${\mathbf{a}}_1=-{\mathrm{\Phi }}_L^T\mathbf{H}\mathbf{G}{\mathbf{F}}_1$ in Eq. (15):

where ${\mathbf{P}}_L^T={\mathbf{I}}_n-{\mathrm{\Phi }}_R{\mathrm{\Phi }}_L^T\mathbf{H}$. Because:

where ${\mathbf{P}}_R={\mathbf{I}}_n-\mathbf{H}{\mathrm{\Phi }}_R{\mathrm{\Phi }}_L^T$, then:

where ${\mathbf{G}}_e={\mathbf{P}}_L^T\mathbf{G}{\mathbf{P}}_R$ is a restricted generalized inverse of $\mathbf{W}$ [10], and ${\mathbf{U}}_R^{\left(1\right)}$ satisfies:

Therefore, the solution of Eq. (11) can be written as:

The computation of matrix ${\mathbf{d}}_1$ need employ the second-order differential information of Eq. (2):

where:

Premultiplying each side of Eq. (20) by ${\mathbf{T}}_L^H$ , yields:

where ${\mathbf{g}}_2={\mathbf{F}}_2+\mathbf{H}{\mathbf{U}}_R\mathrm{\Lambda }\mathrm{\text{'}}\mathrm{\text{'}}$, then:

Using the similar discussion about Eq. (11), one can express the general solution of Eq. (20) as:

where ${\mathbf{U}}_R^{\left(2\right)}={\mathbf{P}}_L^T\mathbf{G}{\mathbf{F}}_2={\mathbf{P}}_L^T\mathbf{G}{\mathbf{P}}_R{\mathbf{F}}_2={\mathbf{G}}_e{\mathbf{g}}_2$. By the relation ${\mathbf{g}}_2={\mathbf{F}}_2+\mathbf{H}{\mathbf{U}}_R\mathrm{\Lambda }\mathrm{\text{'}}\mathrm{\text{'}}$, one has:

Then:

where ${\mathbf{U}}_R^{\left(2\right)}=-\mathbf{W}\mathrm{\text{'}}\mathrm{\text{'}}{\mathbf{U}}_R-2\mathbf{W}\mathrm{\text{'}}{\mathbf{U}}_R^{\left(1\right)}-2\mathbf{H}{\mathbf{U}}_R^{\left(1\right)}\mathrm{\Lambda }\mathrm{\text{'}}-2\mathbf{H}\mathrm{\text{'}}{\mathbf{U}}_R\mathrm{\Lambda }\mathrm{\text{'}}-2\mathbf{M}{\mathbf{U}}_R(\mathrm{\Lambda }\mathrm{\text{'}}{)}^2$. Substituting Eq. (24) into Eq. (21), rearranging the equation yields:

Then we can get the off-diagonal elements of matrix ${\mathbf{d}}_1$:

The diagonal elements of ${\mathbf{d}}_1$ can be determined from Eq. (7). Let ${\mathbf{U}}_R=\left(u_{R_{ij}}\right)$, by Eq. (7) and Eq. (19) one has:

Then:

So:

Repeat the above process with Eq. (12), we have the derivatives of left eigenvectors:

where ${\mathbf{U}}_L^{\mathrm{\text{'}}}=-{\mathbf{G}}_e^T\mathbf{W}{\mathrm{\text{'}}}^T{\mathbf{U}}_L$ and the off-diagonal elements of ${\mathbf{b}}_1$ can be determined by:

where:

Differentiating both sides of Eq. (6) and letting $p\to p_0$, we get:

Then, we complete the process for computing derivatives of eigenvectors when the eigenvalues of Eq. (14) are distinct.

Case 2. Eq. (14) has repeated eigenvalues. Suppose that the eigenvalues of Eq. (14) are ${\lambda }_s^{\text{'}}$ with multiplicity is $m_s$, $(s=1,\cdots ,h)$, then ${\sum }_{s=1}^h\mathrm{‍}{m}_s=r$. The right and left eigenvectors is defined:

Because the eigenvectors are not uniquely determined when eigenvalues have repeated roots, ${\mathrm{\Gamma }}_R$ and ${\mathrm{\Gamma }}_L$, and then ${\mathbf{U}}_R$ and ${\mathbf{U}}_L$ , are not uniquely defined. Let:

where ${\mathbf{Q}}_{R_s}$ and ${\mathbf{Q}}_{L_s}$ are coefficient matrices. Dividing Eq. (26) into $m_s\times m_t$ block forms and substituting Eqs. (34) and (35) into it, one obtains:

where:

Premulitiplying each side of Eq. (37) by ${\mathbf{H}}_{R_s}$ with $s=t$, yields a standard eigenvalue problem:

Suppose the eigenvalues of Eq. (40) are distinct, $\mathrm{\Lambda }\mathrm{\text{'}}\mathrm{\text{'}}$ and ${\mathbf{Q}}_{R_s}$ are uniquely determined to the extent of an non-zero constant multiplier by Eq. (40), then ${\mathbf{U}}_R=({\mathbf{U}}_{R_1},\cdots ,{\mathbf{U}}_{R_h})$, $U_{R_s}={\mathrm{\Phi }}_R{\mathrm{\Gamma }}_{R_s}{\mathbf{Q}}_{R_s}$ are uniquely determined by the normalized condition Eq. (7). By the relation ${\mathbf{Q}}_{L_s}^T{\mathbf{Q}}_{R_s}={\mathbf{I}}_{m_s}$, ${\mathbf{Q}}_{L_s}$ are also determined, and then ${\mathbf{U}}_L$, ${\mathbf{U}}_R^{\left(1\right)}=-{\mathbf{G}}_e\mathbf{W}\mathrm{\text{'}}{\mathbf{U}}_R$ are also uniquely identified by Eqs. (36) and (17). So, the result of ${\mathbf{U}}_{R\mathrm{\text{'}}}={\mathbf{U}}_R^{\left(1\right)}+{\mathbf{U}}_R{\mathbf{d}}_1$ also becomes determination of the off-diagonal elements of ${\mathbf{d}}_1$ because the relation Eq. (30) is also right. On both sides of Eq. (37), we take $s\ne t$:

To extra the off-diagonal elements of ${\mathbf{d}}_1^{ss}$ and use the third derivative of Eq. (2), we obtain following relation by Eqs. (17), (26), (31):

where:

Taking out the diagonal block equation, one has:

Then:

where ${\lambda }_{sj}^{\text{'}\text{'}}$ is the $j$th diagonal element of ${{\mathrm{\Lambda }}_s^{\mathrm{\text{'}}\mathrm{\text{'}}}}_{}$. From Eq. (44), one has:

The derivatives of left eigenvectors can be computed by similar method. Then, we complete the process of computing the derivatives of eigenvectors in two cases. Formally, an algorithm based on the above procedure can be designed as following.

Algorithm procedure for computing the eigenpair derivatives:

Step 1. Input: Matrices $\mathbf{M}$, $\mathbf{C}$, $\mathbf{K}$ and the first to third order derivatives of $\mathbf{M}$, $\mathbf{C}$, $\mathbf{K}$, the repeated eigenvalue ${\lambda }_0$ and corresponding right and left normalized eigenvectors matrices ${\mathrm{\Phi }}_R$, ${\mathrm{\Phi }}_L\in C^{n\times r}$.

Step 2. Compute:

The generalized inverse $\mathbf{G}$ of $\mathbf{W}$ and $\mathbf{G}e=(\mathbf{I}-{\mathrm{\Phi }}_R{\mathrm{\Phi }}_L^T\mathbf{H})\mathbf{G}(\mathbf{I}-\mathbf{H}{\mathrm{\Phi }}_R{\mathrm{\Phi }}_L^T)$.

Step 3. Obtain the eigenvalue derivatives ${{\mathrm{\Lambda }}_i^{\mathrm{\text{'}}}}_{}$ by computing the eigenproblem $\mathbf{D}{\mathrm{\Gamma }}_R={\mathrm{\Gamma }}_R\mathrm{\Lambda }\mathrm{\text{'}}.$

Step 4. When the eigenvalue derivatives ${{\lambda }_i^{\mathrm{\text{'}}}}_{}$ are distinct, then obtain ${\mathbf{U}}_R$, ${\mathbf{U}}_L$ and ${\mathbf{U}}_R^{\left(1\right)}$ by Eqs. (8) and (17), then get ${\mathbf{d}}_1$, by Eqs. (29) and (32).

Step 5. If the eigenvalues of $\mathbf{D}{\mathrm{\Gamma }}_R={\mathrm{\Gamma }}_R\mathrm{\Lambda }\mathrm{\text{'}}$ have repeated roots, calculate:

Solve the eigenproblem ${\mathbf{A}}_{2s}\cdot {\mathbf{Q}}_{R_s}={\mathbf{Q}}_{R_s}\cdot {{\mathrm{\Lambda }}_s^{\mathrm{\text{'}}\mathrm{\text{'}}}}_{}$, compute ${\mathbf{U}}_R$, ${\mathbf{U}}_L$ and ${\mathbf{U}}_R^{\left(1\right)}$ by Eqs. (35) and (17) and ${\mathbf{d}}_1$, by Eqs. (41) and (45), (30).

Step 6. Calculate ${\mathbf{U}}_{R\mathrm{\text{'}}}={\mathbf{U}}_R^{\left(1\right)}+{\mathbf{U}}_R{\mathbf{d}}_1.$

Step 7. Output: ${{\mathrm{\Lambda }}_i^{\mathrm{\text{'}}}}_{}$, ${\mathbf{U}}_{\mathbf{R}}^{\mathit{\text{'}}}$.

The computational cost of the Algorithm is $O\left(n^3\right)$, where the generalized inverse $\mathbf{G}$ of matrix $\mathbf{W}$ is calculated by the singular value decomposition of $\mathbf{W}$.

4. Numerical illustration

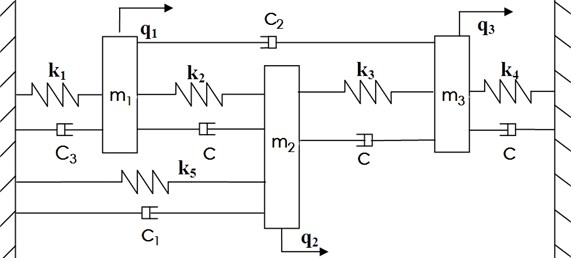
To illustrate the effectiveness of the proposed algorithm, we carried out one numerical example shown in Fig. 1. All the following calculations used MATLAB2015b.

In Fig. 1, there are five springs, four damping and three disks. In order to obtain asymmetric damped system, we suppose that the system is rotated with high speed in a container. From Fig. 1, we can get the mass, stiffness and damping matrices of the system:

We assume that the system has the following gyroscopic matrix:

Fig. 1An asymmetric damped system

Then, we can get the damped matrix of the asymmetric system by the relation:

Setting $m_1=m_2=m_3=$ 1 kg, $k_1=k_4=k_5=$ 1000 N/m, $k_2=k_3=$ 0 N/m, $c_1=c_2=c_3=$ 10 N s/m. We select $c$ as the design parameter and consider $c_0=$ 0. Then:

The eigenvalues of the damped system are ${\lambda }_1={\lambda }_2=–5–31.225i$ at $p=$ 0 and the corresponding eigenvectors are:

By Eq. (12) we have:

This means the derivatives of eigenvalues are equal. Using Eq. (40), we get:

Then we derive the adjacent right and eigenvectors $\mathbf{U}$, $\mathbf{V}$ and the right eigenvectors derivatives $\mathbf{U}{\mathrm{\text{'}}}_R$ as following:

To examine the correctness of the above results, we give the parameter $c$ a small perturbation $\mathrm{\Delta }c=$ 0.1. We compute the eigenpair of perturbed system at $c=c_0+\mathrm{\Delta }c$ and compare the result with the linear approximation of perturbed system by Taylor series. Table 1 and Table 2 show the comparisons of the eigenvalues and eigenvectors.

5. Conclusions

Derivatives of eigenvalues and eigenvectors of parameter-dependent matrix eigenproblems play a key role in the optimum design of structures in engineering. In this paper, we extend the method of [21] to asymmetric damped system and develop a numerical algorithm for computing the eigenpair derivatives by adopting a new normalization to guarantee the uniqueness of the eigenvectors. The proposed algorithm divides the eigenvectors derivatives into a particular solution and a homogeneous solution, where the particular solution to the governing equations is constructed by using the generalized inverse matrix. The present study is the first step for the research of eigensensitivity of damped systems. The higher order derivatives of eigenvalues and eigenvectors will be challenges for further research.