Fault severity detection of ball bearings and efficiency of one-period analysis in early fault diagnosis of rotating machinery

1. Introduction

Condition monitoring and diagnosis of rotating machinery using vibration based sensors have always been a challenging problematic since a highly distinctive fault representation with an acceptable detection performance is hard to achieve especially due to the possibility of multi-fault presence and environmental noise. In addition, it is vital to detect faulty cases in early-phase to maintain its safety and reliability.

Rotating element bearings (REBs) are one of the most common structure in rotating machinery [1]. There are several possible failure modes which effects inside or outside ring of the rolling elements or cage structure. Among all, bearing rolling element fault is the most dominant failure [2] and detection of such kind of failures is maintained by model based and data-driven methods using sensor data.

Various methods have already been proposed in recent literature for fault detection of REBs. Continuous Wavelet Transform (CWT), Gabor wavelets, wavelet transform [3], Hilbert-Huang Transform and Support Vector Machines [4], kurtogram and envelope analysis [5], time-domain analysis in connection to fuzzy C-means [6] and statistical features [7] are proven the efficiency in REBs fault diagnosis.

This paper proposes several methods to diagnose REBs faulty modes in early phase in addition to severity classification of ball bearings on a database which is remarkably focused in the literature over the last decade [1]. Among all techniques utilized in this research, MOMEDA feature extraction scheme is considered to be the most efficient in classifying REBs faults in multi-fault classification of early cases and multi-level fault severity classification.

The organization of this paper is as follows: The database acquired for the research is explained in Section 2. Feature extraction methods and the techniques of extraction of features subjected to this study are given Section 3. Experimental results and the proposed methodology are demonstrated in Section 4. Finally, conclusion part is presented in Section 5.

2. Database and segmentation

Case Western Reserve University provides a database which includes accelerometer based vibration signals that are retrieved by a test rig in laboratory environment. The database has four main classes; healthy case (HC), ball faults (BF), inner race faults (IRF) and outer race faults (ORF) that allows up to four level of severity classification (0.18, 0.36, 0,53, 0,71 mm in diameter) and multi-fault diagnosis of rotating machinery bearings [8]. The datasets utilized in this research include faulty signals which are collected by accelerometer sensors, localized at drive end of deep groove ball bearings of the type 6205-2RS JEM, recorded at 12 kHz and healthy signals of 48 kHz, which then downsampled to 12k sampling rate, may be seen in Table 1. In the segmentation process, three different approaches taken into account; Dataset A is constructed covering five periods of rotation of the motor (5$T$) inspired by the study in [4] and includes 2000 data points in each sample. Datasets B, C and D are generated by preserving one ($T$) and one and a half period (1,5$T$) of rotation of the motor in each sample.

3. Proposed approaches

This section provides information about some of the useful techniques that are subjected to fault classification performance in the experiments throughout this research.

3.1. Wavelet packet analysis

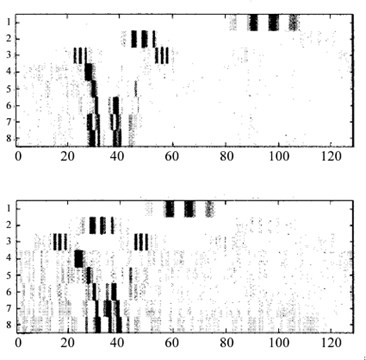
One of the common approach to extract features of vibration signals, a Short Time Fourier Transform based method, wavelet packet analysis is introduced in the literature. Wavelet packaging divides the Fourier spectrum of the signal into desired number of frequency bands which leads to different frequency resolution. Referring to the number of levels, $L$ while $n=2^L$ where $n$ represents the number of components in Wavelet Packet Transform (WPT). Then, filtering is carried out on the signal to obtain low and high frequency components which is followed by down sampling to achieve next level. Referring to Fig. 1, due to being not time-invariant [9], energy calculation of each wavelet packet is performed to rise its immunity to detection of the transients in non-stationary signal processing and Wavelet Packet Energy (WPE) features are achieved (Fig. 2).

In this study, using wavelet packet energy, three level and five level WPE vectors are created and used to train the classifiers.

Fig. 1a) Transient signals shifted in time-domain, b) resultant eight level quantized WPT

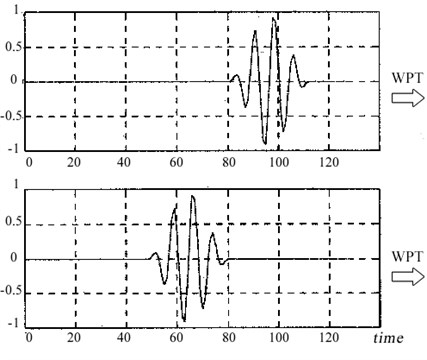
a)

b)

Fig. 2Resultant eight level quantized WPE for the signals in Fig. 1

3.3. Multipoint optimal minimum entropy deconvolution adjusted (MOMEDA)

This method is a further improvement of an iterative algorithm, Minimum Entropy Deconvolution (MED) [10] that is used in fault identification of bearings and gearboxes. MED is capable of deconvolving a single impulse but not an impulse train. Since iterative methods are time consuming, a non-iterative optimal solution for the deconvolution filter, optimal MED (OMED) is presented [11]. The problem with OMED is discontinuity due to zero input signal assumption. Overcoming this issue is possible via using an adaptive recursive (AR) filtering which leads to OMEDA. Nevertheless, it is still inefficient to identify periodic impulses of an input signal related to rotating machinery. For this purpose, a cutting-edge MOMEDA method is presented in the literature that provides deconvolution of infinite number of impulses [12]. MOMEDA is able to solve this problem with optimized computation and resulting MOMEDA spectrum is essential to identify the faulty frequencies which leads to spectral feature extraction in the area of rotating machinery. This method requires using at least five periods (5$T$) of signals in order to work in its highest efficiency.

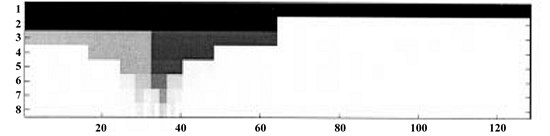
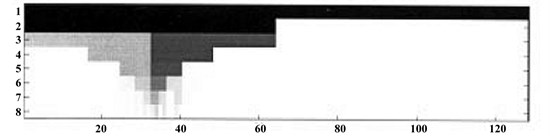
In the process of MOMEDA feature extraction, pre-calculated model based faulty frequencies for different mechanical parts are turned into operating frequencies regarding of the rotational speed of the motor are used (Table 2). In the experiments, window size is chosen as 100 for $T$-1,5$T$ period analyses and 500 for 5$T$ analysis. An example faulty signal feature extraction of ball bearings for the purpose of this research using MOMEDA is shown in Fig. 3.

Table 2Defect frequencies of bearing type 6205-2RS JEM at drive end

6205-2RS JEM	Inner ring	Outer ring	Cage train	Rolling element
Defect Freq. (Hz)	5,4125	3,5848	0,3983	4,7135
Operating Freq. (Hz)	162,01	107,31	11,922	141,10

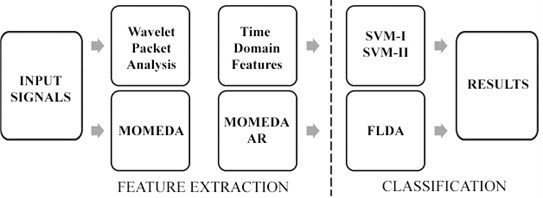
Final implementation of proposed method that is illustrated by Fig. 4 includes autoregressive (AR) filtering [13] with a window size of 50 for pre-whitening the signal before MOMEDA method is applied to increase its efficiency by means of fault detection of 5$T$ segmented signals.

Fig. 3a) Faulty signal of ball bearings and b) resulting MOMEDA signal

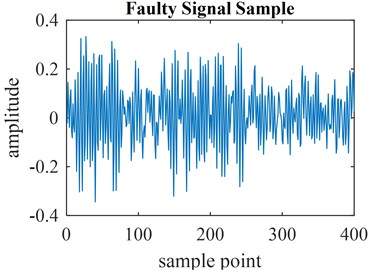
a)

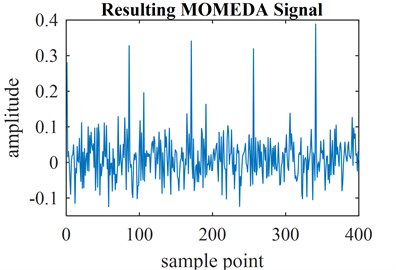
b)

Fig. 4Proposed fault severity and early fault classification scheme of ball bearings of rotating machinery

4. Experimental results

In the analyses, two main objectives are considered. Firstly, severity classification of the rotating elements of bearing faults are investigated including early faults, depending on the period of the rotation of the motor by using Dataset A, B and C. Secondly, a multi-fault diagnosis of early faults of rotating elements is performed on Dataset D using one-period analysis to show its efficiency. Feature extraction includes two different levels of wavelet packet energy (WPE_3, WPE_5), time-domain features (TDF), MOMEDA spectrum (MOMEDA SPEC), MOMEDA with (MOMEDA AR) and without (MOMEDA) AR filtering. Two state of art classifiers; Support Vector Machine with linear (SVM-I) and second order (SVM-II) kernel in addition to Fisher Linear Discriminant Analysis (FLDA) are employed and evaluation process is performed using five (Dataset C) and six (Dataset A, B, D) fold cross-validation which is shown in Table 3 (* represents, using that classifier is either not applicable or dataset is already classified with 100 % success rate with less computational effort). In addition, another experiment is carried out to achieve best results. In the testing process of Dataset A, each sample is tested against remaining ones and average classification accuracy is calculated as seen in Table 4.

Proposed methodology to obtain best results in early diagnosis; Dataset A(1,2), B(1,2), C(1,2) and multi-class classification; A(1-5), B(1-5), C(1-5), D(1-4) is illustrated in Fig. 4.

5. Conclusions

In this study, condition monitoring of rotating machinery is examined upon sub-segmentation of healthy and faulty signals in the database retrieved from CWRU. According to the results, early fault detection including multi faults by the use of MOMEDA features, reaches a highest possible accuracy of 100 % even in one-period analysis. However, in five level severity classification, one-period analysis is not sufficient and maximum of 97,3 % classification success is observed. Another investigation is carried out by using 1,5$T$ analysis and detection success is increased to 98 % on the same dataset with linear SVM kernel. Finally, by utilizing one test sample against all training samples using SVM-II, maximum average accuracy of 99,7 % is reached in bearing fault severity detection, which may be nominated as the most challenging among all RPM levels and fault types according to Table. 6 in the recent study [14]. Proposed methodology for severity classification of ball bearings outperforms the state-of-art techniques specialized for bearing fault diagnosis by means of classification performance and simplicity.