Investigation of effect of acoustic field to coagulation of particles in air flow

Čereška, A.; Tetsman, I.; Maskeliūnas, R.; Grinbergienė, I.; Paškevičius, P.

doi:10.21595/jve.2016.16983

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2016

Check for updates

Investigation of effect of acoustic field to coagulation of particles in air flow

A. Čereška¹

I. Tetsman²

R. Maskeliūnas³

I. Grinbergienė⁴

P. Paškevičius⁵

^{1, 2, 3, 4}Vilnius Gediminas Technical University, Basanavičiaus str. 28, LT-03224, Vilnius, Lithuania

⁵Kaunas University of Technology, Kaunas, 44029, Lithuania

Corresponding Author:

A. Čereška

Cite the article Download PDF

Downloads 1594

WoS Core Citations 2

CrossRef Citations 3

Abstract

In the paper theoretical and experimental investigations of the effect of acoustic field to coagulation of particles in air flow are presented. For the conduction of experimental investigations, a special experimental setup with measurement devices was designed and used. Principle of operation of the proposed experimental setup is presented and the method of conduction of experimental investigations is described. Investigations of effectiveness of coagulation of rigid particles of very small diameter have been performed and dependencies from the sound pressure of the acoustic field and its frequency were investigated. For excitation of the acoustic field two sound generators were used: piezoelectric and aeroacoustic. As a result of the performed investigations it was determined that with the increase of the frequency of acoustic excitation velocity of coagulation of particles increases when the diameter of the particles does not exceed 1 μm. For the most effective coagulation of the particles having the diameter up to 1 μm ultrasonic frequency is required. For the particles with the diameter larger than 1 μm frequency lower than ultrasonic is required. Dependencies of velocity of coagulation of particles from the frequency of acoustic signal and from its amplitude were determined. Initial granulometric constituent parts were compared with the constituent parts obtained after the experimental investigations.

1. Introduction

Main problem in environmental protection is the reduction of spreading of various waste materials. Coagulation is understood as the effect of adhesion of particles to larger units. The main part of the physical model is the description of mechanisms of coagulation. Coagulation because of kinetic interaction of air takes place between the particles which move in the media under the effect of the acoustic field with different velocities and different amplitudes.

In the process of solution of problems of acoustic coagulation, it is possible to determine the main laws of the physical mechanism when particles perform coagulation in the acoustic field. Physical model takes the effect of coagulation into account, which arises because of the ortho kinetic and hydrodynamic mechanisms of acoustic waves [1].

Coagulation because of ortho kinetic interaction takes place between the particles, which move in the acoustic field with different velocities and different amplitudes [2, 3].

The main effect determining the peculiarities of motion of aerosolic particles in the flow is the fact that their weight, when compared with the molecules of the surrounding media, is much bigger (aerosolic particles experience stronger action of the force of inertia than the molecules of the gas) [4, 5].

Reduction of mono- and poly- dispersional aerosolic materials is a very important problem of environmental protection. Acoustic coagulation is suitable for aerosolic materials, the sizes of particles in which are up to 10 μm. But it is not very effective for aerosolic materials with low concentration, this is due to the fact that in them, because of large distances between particles, there is low probability that the hydrodynamic forces will start to act. Equations of motion of the particles are obtained on the basis of the well-known laws of classical hydrodynamics.

Aerosolic particles in the gas media experience the action of external forces, they are the forces of resistance and hydrodynamic forces acting between the particles. External forces include the forces of gravity, electrostatic forces and others. Forces acting to the particle from the moving or immovable media are considered as forces of resistance. When the particles oscillate in the acoustic field forces of resistance may be considered as external forces. In order to determine the regimes of acoustic excitation it is necessary to know the dependence of time of decay of the dispersion system of the gas from the quantities describing this effect, that is from the frequency of acoustic vibrations and from the pressure of sound. Those relationships are determined by the physical qualities of two phases, such as density and pressure of the gas phase, density of the rigid phase and the dispersion interaction of the investigated aerosolic material.

Depending on the size of the particles their initial concentration may be 10⁷-10⁸ g/cm³ and higher. In experimental investigations of the concentration of particles conducted by Parker and Brandt it was determined, that concentration depends on time and the coefficient of coagulation exponentially. The same relationship was also determined by Podashevnikov [6].

When creating models of coagulation of particles, it is important to determine the minimum distance between the particles, starting from which they may coagulate. If it is assumed that the aerosolic particles are distributed uniformly in 1 cm³, the distance between them is determined as described in [7].

The scientists Song [8], Hoffman [9], Ezekoye [10] in the process of investigation of the hydrodynamic component, which is the cause of the probability of collision, determined, that when the particles are small (up to 10 μm) and when the pressure of sound is up to 137 dB, the Reynolds number is smaller than 0.4. Relative velocity of the oscillating particles is near to the relative velocity of motion towards the steady state, then the ortho kinetic collision is not significant. Gravitation is not effective when calculating the kinetic collision length of the air, but it has an acoustic effect [11].

Probabilistic collision of particles in the investigations [12] was calculated according to the interaction mechanisms of two particles: ortho kinetic and hydrodynamic.

It must be noted that the problem of the process of carrying of particles in the gas media includes more different problems than the equations of aerodynamics describe. Motion of particles can take place because of the processes of molecular kinetics in gas media, for example because of the Braun diffusion. At the same time the phenomena of heat and mass exchange may take place, as well as the effect of phase change. All this makes the description of motion of aerosolic materials in gas media much more difficult.

Theory of acoustic coagulation is based on the solution of several physical problems: investigation of the behaviour of a separate particle, of several particles and of a system of smallest particles in the field of sound. In the process of solution of this problem it is possible to investigate the main laws of the physical mechanism when the particles coagulate in the acoustic field.

When the relative velocity of particles is near to the relative velocity of the process of reaching the steady state, the ortho kinetic collision becomes not important.

The purpose of the research is to evaluate the effectiveness of coagulation of aerosolic material and its dependence on the frequency and amplitude of the action of the acoustic field.

2. Mathematical modelling of coagulation of particles

Modelling is performed on the basis of the method of Monte Carlo. When modelling the cohesion of particles in the acoustic field the investigation is based on the equation of Smoluchovsky:

1

\frac{\partial n_{k}}{\partial t} (t) = \frac{1}{2} \sum_{i = 1}^{k - 1} β_{i, k - 1} n_{i} (t) n_{k - 1} (t) - n_{k} \sum_{i = 1}^{\infty} β_{i, k} n_{i} (t),

where $k$ is an integer number from one to infinity, $β_{i, k}$ is the kernel of coagulation, which is independent of time and it is describing the intensity of collisions, $n_{i} (t)$ is the value of $i$ th concentration at the moment of time $t$ .

The first member of the right side of the equation characterizes the intensity of increase of concentration of value of $k$ because of collisions of values of $i$ and $k$ , and the second member describes the decrease of concentration of value of $k$ when there is collision with any particles [12]. The kernel of coagulation is symmetric when $β_{i, k} = β_{k, i}$ .

Modelling indicates that when there are particles of different diameters in the flow (poly dispersional), the ortho kinetic mechanism dominates. The adhesion of two particles may be approximately represented as a sum of two components [12]:

2

β_{i, k} = β_{O i, k} + β_{H i, k},

where $β_{O i, k}$ is the component of coagulation which characterizes the decrease of distance between the particles because of the mechanism of orthokinetic interaction, $β_{H i, k}$ is the component of coagulation which characterizes the decrease of distance between the particles because of the mechanism of hydrodynamic interaction, $i$ and $k$ are values determining the probability of collision of particles [9].

The collision of particles because of the mechanism of hydrodynamic interaction is determined by the hydrodynamic forces of fluid or gas, which take place when two particles are approaching one another. For particles which are in an ideal fluid the function of frequency of collision may be described by the classical expression of Konig [10]:

3

β_{K o n i g}^{H y} = \frac{\sqrt{3} π ρ_{g} U_{g}^{2}}{36 μ_{g}} \frac{d_{1}^{2} d_{2}^{2}}{d_{1} + d_{2}},

where $d_{1}$ and $d_{2}$ are diameters of the particles, $ρ_{g}$ is density of the media, $U_{g}$ is amplitude of the sound wave, $μ_{g}$ is viscosity of the media.

When the mechanism of hydrodynamic interaction is acting the viscosity of the fluid is not significant when particles of large diameter are in it and when there are sound waves of high intensity. By taking this into account the force of hydrodynamic interaction of a single particle consists of two parts. The first part is because of attraction of the first and the second particles with other particles that are in the flow. The attraction interaction takes place because of the rotation of the first and the second particles. The second part reflects the effect of viscous waves. Transfer of particles also influences both parts. Then the function of frequency of hydrodynamic collision is expressed as [13]:

4

β_{S o n g}^{H y} = \frac{\sqrt{3} ρ_{g} U_{g}^{2}}{144 π μ_{g}} \frac{d_{1}^{2} d_{2}^{2}}{d_{1} + d_{2}} g_{12} = (\frac{g_{12}}{4 π^{2}}) β_{K o n i g}^{H y},

where $g_{12}$ is the function of hydrodynamic interaction.

When the mechanism of ortho kinetic interaction is acting collision of particles of different sizes takes place because of their relative motion, which is excited by sound waves. In the acoustic field smaller particles oscillate more freely than the larger ones, as a consequence of this particles of different sizes move differently. The kernel of ortho kinetic collision is expressed as [7]:

5

β_{M e d n i k o v}^{O r} = \frac{1}{2 {(d_{1} + d_{2})}^{2} U_{g} η_{12 p}},

where $η_{12 p}$ is the relative coefficient of attraction between the first and the second particles:

6

η_{12 p} = \sqrt{η_{1 p}^{2} + η_{2 p}^{2} - 2 η_{1 p} η_{2 p} c o s (φ_{1} - φ_{2})},

where $η_{1 p}$ is the coefficient of attraction of the first particle and $η_{2 p}$ is the coefficient of attraction of the second particle, $φ_{1}$ is the phase of oscillation of the first particle, $φ_{2}$ is the phase of oscillation of the second particle.

Relative velocity of vibrations of the amplitude between the two particles has the units of measurement m/s and is determined as [13]:

7

U_{12} = U_{2} - U_{1} = η_{12 g} U_{g},

where $U_{2}$ is amplitude of velocity of the second particle, $U_{1}$ is amplitude of velocity of the first particle, $η_{12 g}$ is the relative coefficient of flow between two different particles, which is calculated as:

8

η_{12 g} = \frac{ω (τ_{1} - τ_{2})}{\sqrt{(1 + {(ω τ_{1})}^{2}) (1 + {(ω τ_{2})}^{2})}},

where $τ_{1}$ is the relaxation time of the first particle and $τ_{2}$ is the relaxation time of the second particle, both relaxation times have the units of measurement s, $ω$ is cyclic frequency of oscillation of the acoustic wave.

Collision of the two particles when acoustic vibrations are acting simultaneously is investigated. Then the biggest distance of separation of particles is determined by the relative displacement of the particle between the two particles. This distance is calculated as:

9

L_{d} = |x_{p 1} - x_{p 2}| = \frac{η_{12 g} U_{g}}{ω},

where $x_{p 1}$ is the amplitude of displacement of the first particle and $x_{p 2}$ is the amplitude of displacement of the second particle.

Near to the large particle the lines of flow of the fluid bend and small particles which are located near to the large ones are directed as shown in Fig. 1. Here $d_{1}$ is the diameter of the large particle, $d_{2}$ is the diameter of the small particle, $y_{c}$ is the critical radial distance of possible collisions of particles, that is it is a maximum radial distance. The critical distance $y_{c}$ determines the effectiveness of collision of particles, which is calculated as:

10

ε = \frac{4 y_{c}^{2}}{{(d_{1} + d_{2})}^{2}} .

If $ε$ is homogeneous, then all small particles collide, that is by the area ${(d_{1} + d_{2})}^{2} / 4$ collide with large particles. Some of the small particles avoid collisions because of the directing trajectories of the particles, which are smaller than homogeneous, so they are controlled by the Stokes number.

Because of the setting down of the small particles $d_{2}$ the effectiveness of collision of the constant flow of large particles $d_{1}$ can be expressed by using the Stokes number:

11

ε = {(\frac{S t}{S t + A})}^{B},

where $A$ and $B$ are constants: $A =$ 0.65 and $B =$ 3.7 (see [14]).

The Stokes number is determined as:

12

S t = \frac{ρ_{p} μ_{12 g} U_{g} d_{2}^{2}}{18 μ_{g} d_{1}},

where $ρ_{p}$ is density of the particle, $μ_{12 g}$ is a coefficient of relative attraction between the two particles.

Fig. 1a) Structural diagram of the process of aglomeration of particles: 1 – ventilation device, 2 – flux of air, 3 – volume for supply of particles, 4 – unseparated particles, 5 – separator of particles of cyclone type, 6 – particles the size of which is greater than 10 μm, 7 – particles of the size up to 10 μm, 8 – channell, 9 – piezoelectric generator of acoustic waves, 10 – acoustic wave, 11 – laser device for registration of size and quiantity of particles, 12 – the aglomerated particles, 13 – volume of the aglomerated particles; b) Collision of particles of small diameter d2 with a large particle having diameter d1 [13], yc is the critical (maximum) radial distance of possible collisions of particles, bending of lines of flow of fluid is schematically represented in the figure

a) Structural diagram of the process of aglomeration of particles: 1 – ventilation device, 2 – flux of air, 3 – volume for supply of particles, 4 – unseparated particles, 5 – separator of particles of cyclone type, 6 – particles the size of which is greater than 10 μm, 7 – particles of the size up to 10 μm, 8 – channell, 9 – piezoelectric generator of acoustic waves, 10 – acoustic wave, 11 – laser device for registration of size and quiantity of particles, 12 – the aglomerated particles, 13 – volume of the aglomerated particles; b) Collision of particles of small diameter d2 with a large particle having diameter d1 [13], yc is the critical (maximum) radial distance of possible collisions of particles, bending of lines of flow of fluid is schematically represented in the figure

a)

b)

Length of ortho kinetic collision:

13

L_{e f f}^{o r t h} = ε L_{d},

where $ε$ is calculated according to the Eq. (11), $L_{d}$ is calculated according to the Eq. (9) and reflects general relative effect of displacement and effectiveness of collision of particles.

Velocity of the process of reaching steady state of the particles under the action of the force of gravity has the units of measurement m/s and is calculated as:

14

V_{S T} = \frac{C_{c} ρ_{p} g d_{p}^{2}}{18 μ_{g}},

where $ρ_{p}$ is density of the particle, $d_{p}$ is diameter of the particle, $g$ is the acceleration of gravity of the earth, $C_{c}$ is the parameter of slippage. When the diameter of the particles is between 0.1 μm and 10 μm, it is calculated as:

15

C_{c} = 1 + \frac{2,52 λ_{g}}{d_{p}},

where $λ_{g}$ is the average free path of the molecules of the gas and it has the unit of measurement m.

Relative velocity of setting down of two particles has the unit of measurement m/s and is expressed as:

16

V_{T S}^{r e} = \frac{C_{c} ρ_{p} g}{18 μ_{g}} (d_{1}^{2} - d_{2}^{2})

It was determined that the ortho kinetic mechanism of collision of two particles is not significant, when the velocity of the vibrating particles is near to the velocity of the process of reaching the steady state by the flow. Gravitation is not significant when calculating the length of ortho kinetic collision.

3. Experimental setup and method of investigations

For the conduction of experimental investigations special experimental setup was designed and produced (see Fig. 2).

Fig. 2Experimental setup: 1 – fan, 2 – cyclone, 3 – chamber, 4 – amplifier, 5 – sound generator, 6 – Toolbox Type PULSE 3560 – B

Experimental setup consists from four zones: A – the zone of coagulation (aglomeration) of particles – acoustic camera, B – zone of observation of concentration of particles, C – zone of supply of particles, D – zone of generation of sound and measurement (see Fig. 3).

For measurement of parameters of the acoustic field the system of measurement of vibrations Bruel&Kjær “Type 9727” was used (see Fig. 3 D). It consists from the software “Type 7910”, multi channell block for data accumulation “Type PULSE 3560 – B”, computer and hydrophone Bruel&Kjær 8104 (sensitivity – 211 dB 1 V/μPa ± 2 dB, frequency response from 0.1 Hz up to 100 kHz + 1.5 / – 6.0 dB; from 0.1 Hz up to 180 kHz + 3.5 / – 12.5 dB; in the horizontal direction ( $x y$ plane) ± 2 dB frequency 100 kHz; in the vertical direction ( $x z$ plane) ± 4 dB frequency 100 kHz).

During the process of investigations in the system of supply of aerosolic particles air is taken by the ventilator and is blown into a cyclone, which delets from the air flow particles larger than 10 μm. By using a doser quartz sand processed into small particles is input to the air flow which is being cleaned, the size of the elements of sand in it is not bigger than 1 μm. Further the air flow with the particles of quartz sand moves through the duct towards the acoustic camera. Before the acoustic camera the pipe is mounted with the analyzer of concentration of aerosolic particles APC ErgoTouch 2 (see Fig. 3) (diameters of particles (6 channells) – 0.3 µm, 0.5 µm, 1 µm, 3 µm, 5 µm, 10 µm; time of measurement – seconds; volume – 0.01 ± 5 % l/min precision).

The device inputs air with a velocity of 2.83 l/m (error ± 5 %). Before starting the investigation the time period of input of air and the duration of measurements are set. Data how many particles there are in 1 m³ of air and of what diameter those particles are is obtained. Those results are calculated by the device automatically.

Fig. 3Schematic representation of the experimental setup: A – zone of aglomeration (coagulation) of aerosolic particles – acoustic camera, B – zone of observation of concentration of aerosolic particles, C – zone of supply of aerosolic particles, D – zone of generation of sound and measurement

Schematic representation of the experimental setup: A – zone of aglomeration (coagulation) of aerosolic particles – acoustic camera, B – zone of observation of concentration of aerosolic particles, C – zone of supply of aerosolic particles, D – zone of generation of sound and measurement

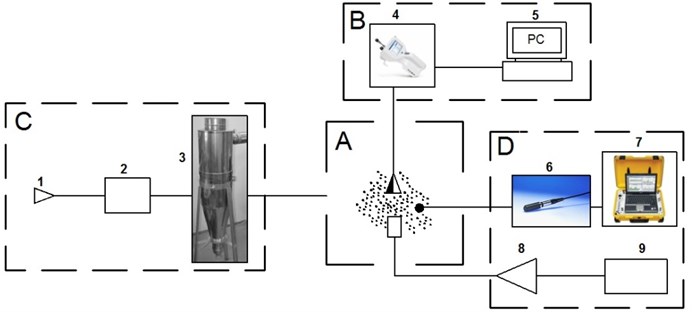
The size and quantity according to fractions of the particles that are in the air flow is fixed before the application of the action of the acoustic field. Air flow with the particles of quartz sand enters into the acoustic camera, in which the flow experiences the action of the acoustic field. This acoustic field is generated by the piezoelectric generator of sound. Then the change of concentration of aerosolic particles is estimated as a function of the time period of action of sound of the acoustic field.

Initial granulometric constituent parts of the particles were determined, as well as granulometric constituent parts of the particles after their separation in a cyclone, in order to ensure that the diameter of the remaining particles does not exceed 10 μm. The analyser of the granulometric constituent parts of the particles CILAS 1090DL was used. Measurement interval was from 0.04 μm up to 500 μm.

For the determination of concentration of the particles optical analyzer of concentration of the particles APS Ergotouch Pro 2 was used.

By using the specialised software frequencies of vibrations registered by the sensor and amplitudes of pressure of sound as functions of time are analyzed. As a result of processing of the results of measurements parameters of the acoustic field were obtained.

Acoustic noise produced by the ventilator is stable in the whole band ~70 dB ± 10 dB. Quartz sand was weighted by using the weighting equipment “BLE – 4”, value of the weighting grade was 0.001 g.

Main parameters of the system which are necessary for the conduction of the experimental investigation are presented in Table 1.

Table 1Main parameters of the system used in the experimental investigation

Parameter	Units of measurement	Value
Quantity of air in the system	m³/h	6-25
Weight concentration of aerosolic materials in air	g/m³	10-45
Time of exposure of aerosolic material in the acoustic camera	s	0.5-3.5
Frequency of sound	kHz	8-24
Level of sound pressure in the acoustic camera	dB	>120

Acoustic field in the acoustic camera is notstable. During the investigation the hydrophone must be mounted in parallel to the direction of propagation of sound waves. This is necessary in order to ensure the highest sensitivity of the hydrophone. Largest pressure of sound was registered nearest to the source of the acoustic field. When the distance to the source of the acoustic field increases the pressure of sound decreases.

4. Results of investigations and discussion

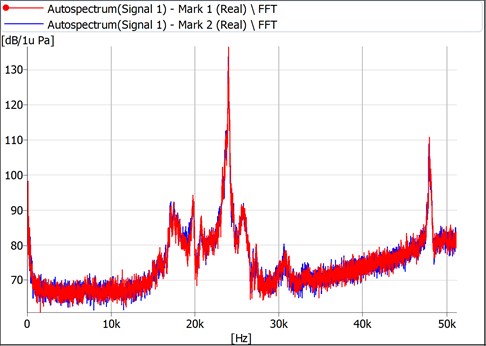
By using the developed experimental setup investigations of effectiveness of coagulation of aerosolic material as functions of pressure of sound and frequency of the acoustic field were performed. In the process of investigations pressure of sound of the acoustic field in the acoustic camera by using the piezoelectric generator of sound was 136.6 dB and frequency was 23.98 kHz. When using the aeroacoustic generator of sound pressure of sound was 138 dB and frequency was 8.08 kHz. Results are presented in Fig. 4 and Fig. 5.

Fig. 4Aeroacoustic generator of sound, pressure of sound 138 dB and frequency 8.08 kHz

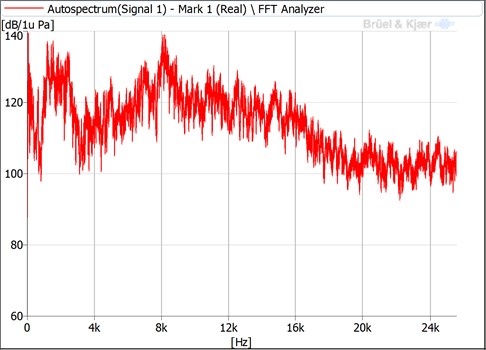
Fig. 5Piezoelectric generator of sound, pressure of sound 136.6 dB and frequency 23.98 kHz

Results of experimental investigations for the system of poly dispersed particles were obtained:

1) When the pressure of sound is 138 dB and the frequency is 8.08 kHz (see Fig. 4) $n / n_{0}$ , (where $n$ is the contrentration of particles after the time $t$ and $n_{0}$ is the initial concentration of particles) it was obtained:

• with the particles of the diameter 0.5 μm varied from 0.42689 up to 0.38807,

• with the particles of the diameter 0.7 μm varied from 0.31703 up to 0.30748,

• with the particles of the diameter 1 μm varied from 0.17752 up to 0.16420,

• with the particles of the diameter 5 μm varied from 0.05664 up to 0.07367,

• with the particles of the diameter 10 μm varied from 0.02193 up to 0.06677;

2) When the pressure of sound is 136.6 dB and the frequency is 23.98 kHz (see Fig. 5) n/n₀:

• with the particles of the diameter 0.5 μm varied from 0.090440575 up to 0.139182893,

• with the particles of the diameter 0.7 μm varied from 0.164726397 up to 0.335110935,

• with the particles of the diameter 1 μm varied from 0.702579154 up to 0.518249834,

• with the particles of the diameter 5 μm varied from 0.022782394 up to 0.000373265,

• with the particles of the diameter 10 μm varied from 0.01947148 up to 0.007829603.

Results of velocity of coagulation of the particles as functions of frequency of sound in time when the pressure of sound is 138 dB and the frequency is 8.080 kHz (by using the aeroacoustic generator of sound) are graphically presented in Fig. 6. Results when the pressure of sound is 136.6 dB and the frequency is 23.980 kHz (by using the piezoceramic generator of sound) are graphically presented in Fig. 7.

Fig. 6Velocity of coagulation of the particles as functions of frequency of sound in time when the pressure of sound is 138 dB and the frequency is 8.08 kHz

Velocity of coagulation of the particles as functions of frequency of sound in time when the pressure of sound is 138 dB and the frequency is 8.08 kHz

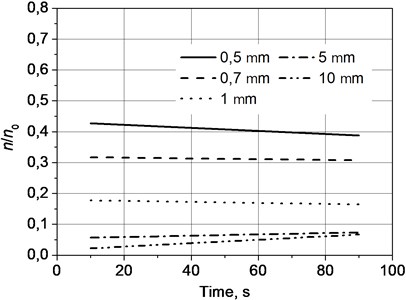
Fig. 7Velocity of coagulation of the particles as functions of frequency of sound in time when the pressure of sound is 136.6 dB and the frequency is 23.98 kHz

Velocity of coagulation of the particles as functions of frequency of sound in time when the pressure of sound is 136.6 dB and the frequency is 23.98 kHz

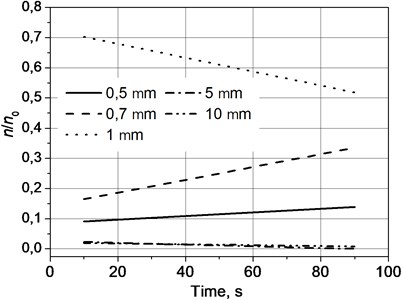
Analysis of the results of investigations showed that for aglomeration of the particles of aerosolic material which are larger than 1 μm, frequency lower than ultrasonic is required. By investigating aglomeration of the particles of aerosolic material which are smaller than 1 μm it was determined that they experience most effective aglomeration in the band of ultrasonic frequencies. If localisation of particles is poly dispersional, then it is necessary to use sound in a wide range of frequencies.

Granulometric constituent parts of quartz sand which was supplied to the system before the cyclone are presented in Fig. 8.

Diameters of particles of quartz sand change from 0.04 μm up to 45 μm. In the same way granulometric constituent parts of the particles which settled in the cyclone were determined in order to check the value of the exact diameter of the particles which can be settled down in a cyclone (see Fig. 9).

Fig. 8Granulometric constituent parts of quartz sand used for the investigation

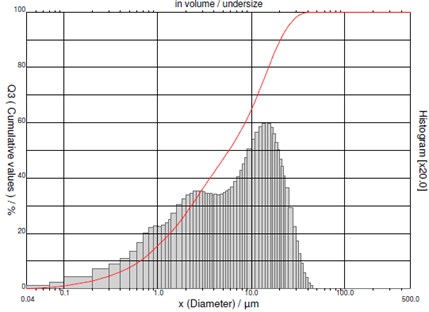
Fig. 9Granulometric constituent parts of particles which settled down in the cyclone

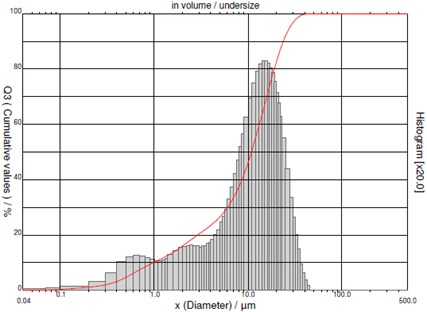
Fig. 10Granulometric constituent parts of the investigated particles

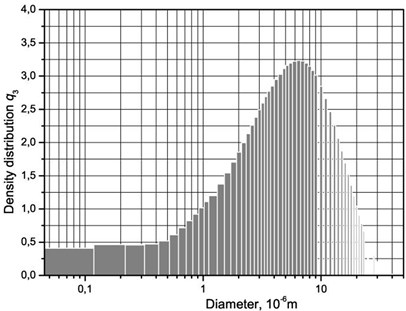
By subtracting the distributions presented in Fig. 8 and Fig. 9 one from another granulometric constituent parts of the investigated particles (which remained after separation in the cyclone) are obtained and shown in Fig. 10.

From the obtained results it was determined that particles which are in the flow and have diameter larger than 10 μm have settled down and thus were separated in the cyclone.

In this work, authors A. Čereška, R. Maskeliūnas and P. Paškevičius have done methodical analysis, data processing and article preparation for printing, I. Tetsman and I. Grinbergienė conducted experiments and mathematical modelling process.

5. Conclusions

1) With the increase of the frequency of the acoustic field velocity of coagulation of particles which are smaller than 1 μm increases.

2) By numerically investigating coagulation of particles in the acoustic field it was determined, that the particles of 10 μm and of 5 μm coagulate with the greatest velocity when the angle of the acoustic signal is 30 degrees and the action of the force of gravity is taken into account. When the force of gravity is not taken into account velocity of coagulation was greatest when the acoustic signal was emitted in the direction of the axis of localisation of particles.

3) For coagulation of particles having the diameter larger than 1 μm frequency lower than the frequencies of the supersonic band is required. Particles which have the diameter which is smaller than 1 μm coagulate most effectively in the band of supersonic frequencies.

4) If the localisation of particles is poly dispersional, it is necessary to use the effect of sound waves in a wide frequency band.

5) In the process of investigation of the interaction of particles of two different diameters (5 μm and 10 μm) under the action of the acoustic field and of the force of gravity, from the relationship of the horizontal acoustic signal with the force of gravity the decrease of the speed of the process of aglomeration and the increase of the time of aglomeration were noticed. At the same time when investigating the aglomeration of two particles of equal diameters such interaction was not noticed.

6) Variation of the frequency of the acoustic signal when the amplitude of the acoustic wave remains the same, does not have substantial influence to the time of aglomeration of the particles. At the same time the time of aglomeration of the particles becomes substantially smaller when the amplitude of the sound waves increases, while the frequency of the acoustic signal remains the same.

References

Yun Z., Xinwu Z., Changchao G. Experimental research on acoustic agglomeration of fine aerosol particles in the standing-wave tube with abrupt section. The Journal of the Acoustical Society of America, Vol. 135, Issue 4, 2014, p. 2375.

Publisher
Liu J., Zhang G., Zhou J., Wang J., Zhao W., Cen K. Experimental study of acoustic agglomeration of coal-fired fly ash particles at low frequencies. Powder Technology, Vol. 193, Issue 1, 2009, p. 20-25.

Publisher
Markauskas D., Kačianauskas R., Maknickas A. Numerical particle-based analysis of the effects responsible for acoustic particle agglomeration. Advanced Powder Technology, Vol. 26, Issue 3, 2014, p. 698-704.

Publisher
Shalunov А., Khmeliov V., Shalunova K. Acoustic Coagulation of Aerosol. Lambert Academic Publishing, 2012, p. 272.

Search CrossRef
Vekteris V., Strishka V., Ozarovskis D., Mokshin V. Experimental investigation of processes in acoustic cyclone separator. Advanced Powder Technology, Vol. 25, Issue 3, 2014, p. 1118-1123.

Publisher
Chernov N. N. Hydrodynamic interaction of an ensemble of weighted particles in a sound field. Materials of the Third All-Russian Scientific Conference with International Participation, Taganrog, News of TRTU, Vol. 5, 2004, p. 115-117, (in Russian).

Search CrossRef
Mednikov E. P. Acoustic Coagulation and Precipitation of Aerosols. Consultant, New-York, 1963.

Search CrossRef
Song L., Koopmann G. H., Hoffmann T. L. An improved theoretical model of acoustic agglomeration. Journal of Vibration and Acoustics, Vol. 116, Issue 2, 1994, p. 208-214.

Publisher
Hoffmann T. L. Environmental implication of acoustic aerosol agglomeration. Ultrasonic, Vol. 38, 2000, p. 353-357.

Publisher
Ezekoye O. A., Wibowo Y. W. Simulation of acoustic agglomeration processes using a sectional algorithm. Journal of Aerosol Science, Vol. 30, Issue 9, 1999, p. 1117-1138.

Publisher
Hoffman T. L. An extended kernel for acoustic agglomeration simulation based on the acoustic wake effect. Journal of Aerosol Science, Vol. 28, Issue 6, 2006, p. 919-936.

Publisher
Sheng Ch., Shen X. Modelling of acoustic agglomeration processes using the direct simulation Monte Carlo method. Journal of Aerosol Science, Vol. 37, Issue 1, 2006, p. 16-36.

Publisher
Dong S., Lipkens B., Cameron T. M. M. The effects of orthokinetic collision, acoustic wake, and gravity on acoustic agglomeration of polydisperse aerosols. Journal of Aerosol Science, Vol. 37, Issue 4, 2006, p. 540-553.

Publisher
Löffler F. Dust Precipitation. George Thieme Verlag, Stuttgart – New York, 1988, (in German).

Search CrossRef

Cited by

Improving the separation efficient of particles smaller than 2.5 micrometer by combining ultrasonic agglomeration and swirling flow techniques

Vladimir N. Khmelev | Andrey V. Shalunov | Viktor A. Nesterov | Hongbing Ding

(2020)

Advanced Manufacturing Processes

Ivan Pavlenko | Oleksandr Liaposhchenko | Vsevolod Sklabinskyi | Vitalii Ivanov | Marek Ochowiak

(2020)

MODELLING OF PARTICLES AGLOMERATION IN THE ACOUSTIC FIELD / DALELIŲ AGLOMERACIJOS AKUSTINIAME LAUKE MODELIAVIMAS

Irina Grinbergienė | Audrius Čereška

(2017)

About this article

Received

09 December 2015

Accepted

15 March 2016

Published

15 May 2016

SUBJECTS

Acoustics, noise control and engineering applications

DOI

https://doi.org/10.21595/jve.2016.16983

Keywords

acoustic field

frequency of sound

aerosolic particles

coagulation

Acknowledgements

A part of Experimental Equipment of this Research was funded by the Project of Scientific Groups (Lithuanian Council of Science), Contract No. MIP-072/2013.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2020 04 02

Numerical investigation of sound transmission loss of circular plates embedded with acoustic black hole

Xiaofei Du, Jianrun Zhang

Research article

2018 10 19

Parametric study of unsteady-flow-induced volute casing vibro-acoustics in a centrifugal fan

Jianhua Zhang, Wuli Chu, Yi Lv

Research article

2017 12 01

Vibroacoustic handling and levitation of microparticles in air

Vytautas Ostasevicius, Vytautas Jurenas, Rimvydas Gaidys, Ievgeniia Golinka

Research article

2017 09 30

Systematical research on the aerodynamic noise of the high-lift airfoil based on FW-H method

Cun Dong Tang, Zhi Ping Wang, Yu Zhou Sima

A. Čereška, I. Tetsman, R. Maskeliūnas, I. Grinbergienė, and P. Paškevičius, “Investigation of effect of acoustic field to coagulation of particles in air flow,” Journal of Vibroengineering, Vol. 18, No. 3, pp. 2004–2015, May 2016, https://doi.org/10.21595/jve.2016.16983

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16983
UR  - https://doi.org/10.21595/jve.2016.16983
TI  - Investigation of effect of acoustic field to coagulation of particles in air flow
T2  - Journal of Vibroengineering
AU  - Čereška, A.
AU  - Tetsman, I.
AU  - Maskeliūnas, R.
AU  - Grinbergienė, I.
AU  - Paškevičius, P.
PY  - 2016
DA  - 2016/05/15
PB  - JVE International Ltd.
SP  - 2004-2015
IS  - 3
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{_ere_ka_2016,
	doi = {10.21595/jve.2016.16983},
	url = {https://doi.org/10.21595/jve.2016.16983},
	year = 2016,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {3},
	pages = {2004--2015},
	author = {A. {\v{C}}ere{\v{s}}ka and I. Tetsman and R. Maskeli{\={u}}nas and I. Grinbergien{\.{e}} and P. Pa{\v{s}}kevi{\v{c}}ius},
	title = {Investigation of effect of acoustic field to coagulation of particles in air flow},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]A. Čereška, I. Tetsman, R. Maskeliūnas, I. Grinbergienė, and P. Paškevičius, “Investigation of effect of acoustic field to coagulation of particles in air flow,” Journal of Vibroengineering, vol. 18, no. 3, pp. 2004–2015, May 2016, doi: 10.21595/jve.2016.16983.

Copy IEEE

Copied to clipboard!

Čereška, A., I. Tetsman, R. Maskeliūnas, I. Grinbergienė, and P. Paškevičius. “Investigation of Effect of Acoustic Field to Coagulation of Particles in Air Flow.” Journal of Vibroengineering 18, no. 3 (May 15, 2016): 2004–15. https://doi.org/10.21595/jve.2016.16983.

Copy Chicago

Copied to clipboard!

Investigation of effect of acoustic field to coagulation of particles in air flow

Abstract

1. Introduction

2. Mathematical modelling of coagulation of particles

3. Experimental setup and method of investigations

4. Results of investigations and discussion

5. Conclusions

References

Cited by

About this article

Related Articles