Study on wheel-rail interaction based on rail roughness

Du, Linlin; Liu, Weining

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

Study on wheel-rail interaction based on rail roughness

Linlin Du¹

Weining Liu²

^{1, 2}Beijing Jiaotong University, Beijing, China

Corresponding Author:

Linlin Du

Cite the article Download PDF

Downloads 1323

Abstract

Environmental vibration and noise pollution caused by the operation of subway is a hot topic of concern at home and abroad. There is a need to research dynamic interaction between trains and track in order to solve environmental vibration and noise pollution caused by the operation of train. As an excitation source of the train vibration, rail surface roughness has significant impact on the wheel-rail interaction. In order to study the effect of rail roughness on the wheel-rail vibration load, the wheel-rail interaction model is established based on excitation of rail surface roughness in this paper. The effect of rail roughness on train vibration load is calculated by this model according to the measured rail roughness data in Beijing subway in the MATLAB program. Wheel-rail force in the most adverse situations is also calculated. The property of wheel-rail force under different conditions such as track forms, driving speed and curve radius is also analyzed in this paper.

1. Introduction

Rail transit is the fundamental way to solve traffic congestion in public and is favored by big cities all over world. Environmental vibration and noise pollution caused by rail transit draw people attention at the same time [1]. For example, the normal life of residents along railways is affected greatly by train induced environmental vibration in Beijing. Therefore, various forms of damping track are adopted to mitigate environmental vibration. However, the abnormal rail corrugation appears in the damping track section also affect the normal operation of Beijing subway. Abnormal corrugation intensified wheel-rail interaction and reduced the life of rail greatly. The wheel-rail whistle noise induced by corrugation is also very serious [2].

Urban Rail Transit Network Planning and construction must face and solve environmental vibration and noise caused by the operation of subway trains, and the root of the problem lies in interaction between vehicle and rails [3]. As an excitation source of the train vibration, rail surface roughness has significantly impact on the wheel-rail interaction. In order to study the effect of rail roughness on wheel-rail vibration load, the wheel-rail interaction model is established based on excitation of rail surface roughness in this paper. The effect of rail roughness on train vibration load is calculated. The property of wheel-rail force under different conditions such as track forms, driving speed and curve radius is also analyzed in this paper.

2. Rail surface roughness and measurement

Rail surface roughness refers to the small valley irregularities on rail surface. Rail roughness can reflect the rail corrugation level. The smaller of rail roughness value, the smoother of rail surface. It is defined as follows:

1

R_{a} = \frac{1}{l} \int_{0}^{l} |y| d x,

where $R_{a}$ represents value of rail roughness, $y$ represents amplitude of roughness in each test point, $l$ represents length of test section.

Rail surface roughness measurement method is divided into indirect measurement method and direct measurement method. Calculation data used in this paper is continuous data measured by the direct measurement method. Continuous data is measured by digital measurement and analysis car, as shown in Fig. 1. Sample data measured by continuous measurement are relative value with respect to the start point and it is a stochastic process associated with longitudinal direction of rail line. The stochastic process is superposition by random irregularity wave with different wavelengths, phases and amplitudes. Usually it can be represented by the statistical parameters according to stochastic theory.

Fig. 1Continuous measurement of rail roughness

3. Wheel-rail interaction model

Based on the number of fixed load model, vehicle balance equation is established and solved in the frequency domain. Input the amplitude of measured roughness data in the model, finally, the wheel-rail interaction load property is obtained.

3.1. Calculation model and parameters

Vertical vehicle vibration is the main consideration when researching environmental influence of vibration induced by subway train. Side roll and lateral vibration of the train is ignored in the model. The vehicle can be simplified to the combination of a series of secondary suspension system. One simplified model of the secondary suspension is shown in Fig. 2. Track is treated as rigid in this model [4]. Assuming that vehicle wheel is contact with rail closely and the rail surface roughness amplitude equals to the actual displacement of wheel. The wheel-rail coupled model is excited by rail roughness measured data in Beijing subway.

Fig. 2Simplified model of vehicle for its vertical vibration

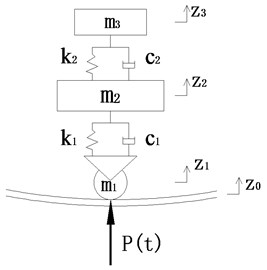
Vehicle parameters in the model can be selected in Table 1, as is shown in follows: $m_{1} =$ 1700 N⋅s²/m, $m_{2} =$ 1800 N⋅s²/m, $m_{3} =$ 10750 N⋅s²/m, $k_{1} =$ 4.9×10⁶ N/m, $k_{2} =$ 2.08×10⁶ N/m, $c_{1} =$ 0.48×10⁶ N⋅s/m, $c_{2} =$ 0.48×10⁶ N⋅s/m.

Table 1Vehicle parameters in Beijing subway

Vehicle mass $M$ (t)	43.0	Spring constant of bogie $k_{T}$ (kN/m)	2080
Inertia moment of vehicle mass $J$ (tm²）	1700	Bogie damping $C_{T}$ (kN⋅S/m)	240
Bogie mass $M$ (t)	3.60	Spring constant of wheelsets (kN/m)	2450
Inertia moment of bogie mass $J$ (tm²)	9.62	Wheelsets damping $C_{T}$ (kN⋅S/m)	240
Length of vehicle $L$ (m)	19.52	distance between bogie centers $l$ (m)	12.66
Axis spacing $a$ (m)	2.30	Wheelsets mass $m_{w}$ (t)	1.70

3.2. Calculation of wheel-rail dynamic load

According to Fig. 2, vehicle balance equation in vertical direction is established:

2

\{\begin{array}{l} m_{3} {\ddot{z}}_{3} + c_{2} ({\dot{z}}_{3} - {\dot{z}}_{2}) + k_{2} (z_{3} - z_{2}) = 0, \\ m_{2} {\ddot{z}}_{2} + c_{1} ({\dot{z}}_{2} - {\dot{z}}_{1}) + k_{1} (z_{2} - z_{1}) - k_{2} (z_{3} - z_{2}) - c_{2} ({\dot{z}}_{3} - {\dot{z}}_{2}) = 0, \end{array}

where $m$ represents mass, $k$ represents rigidity, $c$ represents damping, $z$ represents displacement. Subscripts denote parts can be seen in Fig. 2. Acceleration of wheel, bogie and vehicle is ${\ddot{z}}_{1}$ , ${\ddot{z}}_{2}$ , ${\ddot{z}}_{3}$ , respectively.

After Fourier transforming of Eq. (2), balance equation of vehicle motion in the frequency domain is obtained as follows [5]:

3

\{\begin{array}{l} m_{3} (- ω^{2} {\hat{z}}_{3}) + c_{2} (i ω {\hat{z}}_{3} - i ω {\hat{z}}_{2}) + k_{2} ({\hat{z}}_{3} - {\hat{z}}_{2}) = 0, \\ m_{2} (- ω^{2} {\hat{z}}_{2}) + c_{1} (i ω {\hat{z}}_{2} - i ω {\hat{z}}_{1}) + k_{1} ({\hat{z}}_{2} - {\hat{z}}_{1}) - k_{2} ({\hat{z}}_{3} - {\hat{z}}_{2}) - c_{2} (i ω {\hat{z}}_{3} - i ω {\hat{z}}_{2}) = 0, \end{array}

where ${\hat{z}}_{1},$ ${\hat{z}}_{2},$ ${\hat{z}}_{3}$ represents displacement of wheel, bogie, vehicle in frequency domain, respectively.

Displacement of wheel ${\hat{z}}_{1}$ in the frequency domain can be obtained by Fourier transform on the measured rail roughness data. Specific operating method is explained clearly in the following section. Interacting load between wheel and rail can be calculated by the following formula:

4

P (t) = (m_{1} + m_{2} + m_{3}) g + m_{1} {\ddot{z}}_{1} + m_{2} {\ddot{z}}_{2} + m_{3} {\ddot{z}}_{3} .

3.3. Input of rail surface roughness

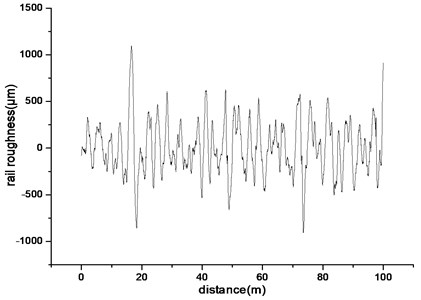
The wheel-rail interaction model is excited by measured data of rail surface roughness in Beijing. Fig. 3 shows rail roughness varies with position, and the horizontal axis represents the test point location, the vertical axis represents the value of rail roughness.

The stochastic process is superposition by random irregularity wave with different wavelengths, phases and amplitudes [6]. Since displacement of the wheel is equal to the magnitude of rail roughness, it can be written as:

5

z_{1} = \sum_{j = 1}^{N} A_{j} e^{- i λ_{j} x},

where $A_{j}$ represents amplitude of rail roughness in given frequency, $λ_{j}$ represents spatial frequency, $x$ represents location of test point, it can also be expressed as $x = v t$ , $v$ represents speed of vehicle.

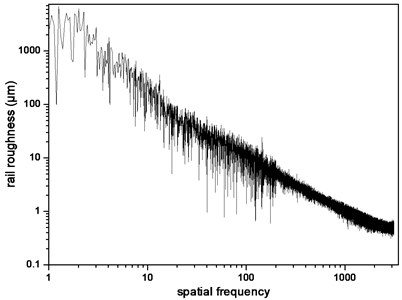
The test data in Fig. 3 is transformed by Fourier to obtain the relationship between roughness amplitude and wave number in spatial frequency domain, as shown in Fig. 4. To calculate the worst case of wheel-rail interaction force caused by rail roughness, take the horizontal and vertical coordinates at the peak point as spatial frequency and roughness amplitude in the harmonic vibration which is used to simulate the motion of vehicle with maximum load.

Fig. 3Measured rail roughness

The Eq. (5) can be simplified as:

6

z_{1} = A_{k} e^{- i λ_{k} v t},

where $λ_{k}$ , $A_{k}$ is the horizontal and vertical coordinates at the peak point at test point in the spatial frequency domain, respectively.

Therefore, the wheel acceleration is:

7

z_{1} = A_{k} {(λ_{k} v)}^{2} e^{- i λ_{k} v t} .

Fig. 4Rail roughness in spatial frequency

4. Calculation and analysis of wheel-rail force

Based on the wheel-rail interaction model described above, the influence of speed, curve radius and type of track on the vehicle vibration is calculated and analyzed in this section.

4.1. The influence of vehicle speed

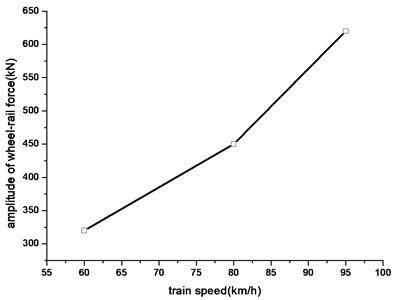
The measured roughness data in straight line with common track type with vehicle velocity 60 km/h, 80 km/h and 95 km/h are selected to analysis the influence of train speed. Roughness data with different speed is shown in Fig. 5. Relationship between amplitude of wheel-rail force and vehicle speed is shown in Fig. 6.

As it can be seen from Fig. 6 that wheel-rail force has a positive correlation with train speed, the faster the vehicle speed, the greater the wheel-rail forces is.

Fig. 5Rail roughness with different speed

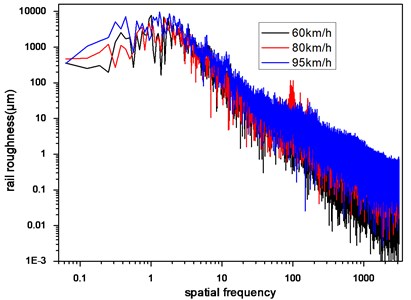
Fig. 6Relationship between amplitude of vibration load and speed

4.2. The influence of curve radius

Inuence of curve radius on the train vibration load is very complex. Wheel-rail force is varying with the running speed of train because it is different under different curve radius. Since the superelevation in curve segment, rail roughness and wheel-rail forces in inner and outer rail of the track will be different. Ignoring wheel-rail force difference between inner and outer rail caused by superelevation setting, the inner rail roughness data in curve segment is adopted for calculating. The selected roughness data is shown in Fig. 7. As it can be seen from Fig. 7 that the smaller the radius, the larger roughness of rail.

Fig. 7Rail roughness with different curve radius

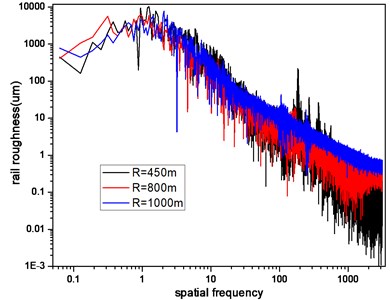
Fig. 8Relationship between amplitude of vibration load and curve radius

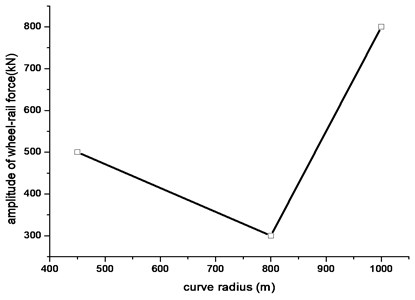
Relationship between amplitude of vibration load and curve radius is shown in Fig. 8. As it can be seen from Fig. 8 that maximum wheel-rail force occurred in segment with radius of 1000 m. Speed of train is different in different curve radius and the greater the radius of curve, the greater of train speed. Wheel-rail interacting force in curve segment is affect by velocity and rail roughness. Since the rail roughness in the section with radius of 450 m is bigger, the amplitude of wheel-rail force is larger than the section with radius of 800 m.

4.3. The influence of track type

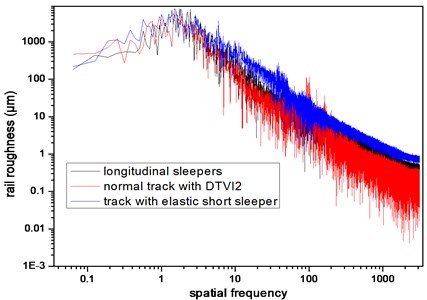
Three types of tracks are analyzed in this section, which is normal track with DTVI2 fasteners, track with longitudinal sleeper and track with elastic short sleeper. Rail roughness data for calculation of three track types is shown in Fig. 9, as it is shown that difference of rail roughness amplitude of track is very small. Rail roughness amplitude in normal track with DTVI2 fasteners is the smallest and the track with elastic short sleeper is the biggest.

Calculating results shows that wheel-rail force in track with longitudinal sleeper is about 1000 kN, which is the largest, wheel-rail force in normal track is about 730 kN, which is the smallest.

Fig. 9Rail roughness with different track types

5. Conclusions

Wheel-rail dynamic interaction model is established based on excitation of rail surface roughness and the interacting force under different conditions is calculated and analyzed in this paper. Conclusions are found as follows:

1. Rail roughness has significant influence on vehicle dynamic load and the wheel-rail force is a positive correlation with the rail roughness, that is the bigger the rail roughness amplitude, the greater the wheel-rail forces.

2. The increase of vehicle speed will lead to the increase of wheel-rail forces.

3. Influence of curve radius on the train vibration load is very complex. As the radius of curve is small, the influence of rail roughness on interaction load is obviously.

References

Ding Deyun Study on Low Frequency Characteristics of Environmental Vibrations due to Metro Trains. Beijing Jiaotong University, Beijing, 2009.

Search CrossRef
Liu Weining, Ren Jing, et al. In-situ tests and analysis on rail corrugation of Beijing metro. Urban Rapid Rail Transit, Vol. 24, Issue 3, 2011, p. 6-9.

Search CrossRef
Li Kefei, Liu Weining, et al. In-situ test and analysis on the vibration mitigation measures of the elevated line in Beijing metro line 5. China Railway Science, Vol. 30, Issue 4, 2009, p. 25-29.

Search CrossRef
Sun Xiaojing Prediction of Environment Vibrations Induced by Metro Trains and Mitigation Measures Analysis. Beijing Jiaotong University, Beijing, 2008.

Search CrossRef
Jia Yingxuan Study on Analytical Model of Coupled Vehicle and Track and Effect to Environment by Metro Train-Induced Vibrations. Beijing Jiaotong University, Beijing, 2009.

Search CrossRef
Xia He Dynamic Interaction between Vehicles and Structures. Science Press, Beijing, 2005.

Search CrossRef

About this article

Received

Accepted

28 July 2015

Published

18 September 2015

SUBJECTS

Vibration in transportation engineering

Keywords

rail roughness

rail corrugation

wheel-rail force

property of dynamic load

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.