Modal analysis of the triple-tower twin-span suspension bridge in deck unit erection stage

2.1. Features of TTTS suspension bridge

Ma’anshan Bridge spans over the Yangtze River in Ma’anshan city, Anhui, China, with a span arrangement of 360+2×1080+360 m, as shown in Fig. 1.

The two main cables of 35 m apart are made of galvanized high-tensile steel wires with a diameter of 5.2 mm and an ultimate tensile strength of 1670 MPa by prefabricated parallel-wire strands (PPWS). Each main cable consists of 154 strands and each strand weight 49 ton with 91 wires built into it. The outer diameter of each main cable is approximately 0.688 m. The double hanger rope is also made of high-tensile galvanized parallel wire bundles. Each hanger is composed of 109 parallel steel wires with a diameter of 5.0 mm and an ultimate tensile strength of 1670 MPa. The spacing between two adjacent hangers is 16.0 m while the separation distance from tower center to the nearest hanger is 20.0 m.

Fig. 1General layout of Ma’anshan Yangtze River bridge (unit: m)

The mid-tower and two side towers are portal-type frames with two cross-beams installed between two tower legs. The height of tower is 178.8 m measured from the top surface of the pile cap to the pylon top. Besides 10.5 m decoration segment part at top, the 127.8 m steel upper part from the bottom of the saddle downwards of the mid-tower is connected to the 40.5 m lower concrete part by the steel-concrete connection joint segments just beneath the bottom steel cross-beam. The center-lines of the tower legs are 35 m apart at the top tower increasing to 43.5 m at the pile cap. The width of the leg is constant at 6 m in the tower plane, but in the plane of bridge tapers from 11 m at top steel-concrete joint section to 7 m at the top tower. For the pre-stressed reinforced concrete bottom tower, the widths reduces from 12 m in tower plane and 25 m in bridge plane at the pile cape to 9.2 m and 17 m at the joint section, and the corresponding thickness is 1.6 m and 2.0 m of the box section respectively. As for the side towers, the width of the legs are both constant at 6 m in tower plane and at 8 m in the plane of bridge, the other sizes is nearly the same with those of the mid-tower.

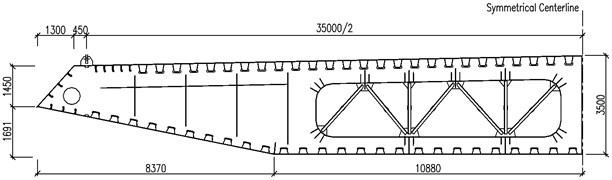
A flat streamlined steel box deck is chosen as the stiffening girder of the bridge, as shown in Fig. 2. The top and bottom inclined webs are set in deck to constituting a wind guide for achieving aerodynamic stability. The overall width of deck is 38.5 m and the deck depth is 3.5 m but 6.0 m near the fixed joint between deck and the lower cross-beam of the tower. The length of standard deck unit is 16 m long with five diaphragms spaced at 3.2 m wide. The standard diaphragm plate is a truss made up of the angle steel L125×125×12 m by welding gusset plate but a plank at the joint between tower and deck. The thickness of top flange in the standard box deck unit is 14 mm and the bottom flange thickness is 10 mm, but 20 mm and 24 mm respectively near mid-tower. The closed U ribs are set into the top and bottom flange.

Fig. 2Standard section of steel box deck of Ma’anshan Yangtze River bridge (unit: mm)

2.2. Finite element modeling

MIDAS/Civil finite element software package is used to simulate the deck erection process of the tower-cable-deck system. The FE model of the TTTS suspension bridge in finished stage is established by the precise balance analysis function for suspension bridges in this software, as shown in Fig. 3. In this model, the stiffening girder and towers are modelled by using the three dimensional Timoshenko beam element. All main cables and hangers are divided into truss elements with initial tensile force. The connections between the stiffening deck units aligned at the center line of top flange and the hangers are simulated with the rigid arm elements, creating the fish-bone finite element model. The model has a total of 1177 elements and 913 nodes. When the weight of the deck is added stepwise to the main cable, large displacements and changes of curvature occur, and the joints between the segments of decks are therefore initially left open to avoid excessive bending of the girder sections. Therefore, each connection between the neighbor segments is modelled as hinge joints in the FE model, while in finished stage each opening is closed thus all segments are lined up to a girder. The elastic connections between the stiffening girder node and the near pylon node are used to simulate the girder set on the cross-beam of main tower.

For the Ma’anshan Yangtze River suspension bridge the girder is erected from the midspans of the two main spans towards the pylons symmetrically. The tower-cable-deck system of the 40 % erection progress is shown in Fig. 4. To simulate the segments lifting procedure in finite element model, the backwards method is used by which the supports, the stiffening girder units and all hangers are dismantled step by step at a reverse construction procedure from the final stage FE model to get FE model in each erection stage. Furthermore, the lumped masses for each of the four pairs of the lifting gantries, estimated to be 2.5×10⁵ kg, was add to the corresponding nodes in the FE model.

Fig. 3FE model for Ma’anshan Yangtze River bridge

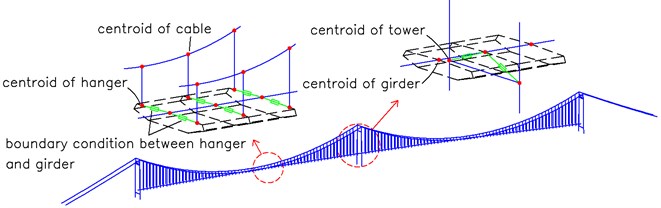
Fig. 4The 40 % erection state of the stiffening girder for Ma’anshan Yangtze River bridge

3.1. Local cable-dominated modes of vibration

The primary modes of the tower-cable-deck system when 10 % segments were lifted are listed in Tables 1 to 5, it is clearly that the uncoupling vibration modes can be reasonably separated into in-plane and out-plane modes. Most of the modes are strong related to the vibration of main cables thus can be called cable-dominated modes. The in-plane modes (in-phase and out-of-phase of the two main cables in the same span, symmetry and anti-symmetry of the neighboring-span cables, and their corresponding combinations) can be classified into groups. Specifically, every four vibration modes goes into one group. For instance, the No. 1 to No. 4 modes in Table 1 can be divided into a group in which the No. 1 is in-phase and double spans symmetry mode. The No. 2 is double spans anti-symmetry mode. But the No. 3 and No. 4 are both out of phase modes with one symmetry and the other anti-symmetry. Moreover, in each group, the in-phase vibration modes of two cables lead to the lift mode of decks such as the No. 1 and No. 2 mode in Table 1, and the out-of-phase modes excite the torsional mode of decks as in the cases of the No. 3 and No. 4 mode in the vertical direction.

The out-of-plane vibration sway modes are listed in Table 2, it is obvious that every four modes can also be divided into one group. In the lateral direction, the in-phase vibration modes between the two main cables induce the lateral sway modes of the suspended deck units while the out-of-phase modes excite the pure cable lateral sway modes without deck motions. It is clearly that, from Tables 1 and 2, the vibration modes of the main cables are restricted by the stiffening decks erected. Because of the interaction between the deck units and the main cables, the vibration of the main cable can result in corresponding motions of the deck units and in turn increasingly erected deck units would be expected to gradually change the modal characteristics of the main cable. The modal characteristics of the temporary tower-cable-deck system are unstable as the construction progresses.

Table 1In-plane vibration modes of cables after 10 % deck erection

No.	Frequencies (Hz)	Cable-dominated in-plane mode shapes	Remarks
1	0.1257		1st cable-dominated deck lift mode
2	0.1257		2nd cable-dominated deck lift mode
3	0.1496		1st cable-dominated deck torsion mode
4	0.1496		2nd cable-dominated deck torsion mode
5	0.1787		3rd cable-dominated deck torsion mode
6	0.1804		4th cable-dominated deck torsion mode
7	0.2168		3rd cable-dominated deck lift mode
8	0.2168		4th cable-dominated deck lift mode

Table 2Out-of-plane vibration sway modes after 10 % deck erection

No.	Frequencies (Hz)	Cable-dominated lateral sway mode shapes	Remarks
1	0.0485		1st cable-dominated sway mode
2	0.0487		2nd cable-dominated sway mode
3	0.1268		1st pure cable sway mode
4	0.1268		2nd pure cable sway mode
5	0.1281		3rd cable-dominated sway mode
6	0.1285		4th cable-dominated sway mode
7	0.1326		3rd pure cable sway mode
8	0.1327		4th pure cable sway mode

3.2. Local towers and stiffening decks dominated modes of vibration

Besides most of the local cable dominated modes, there also exist some local modes dominated by the tower and stiffening decks because of the interactions among the separate structures. The side and middle tower-dominated modes of vibration are listed in Table 3 respectively. It is interesting that all the bending and torsional modes of side towers are out-of-phase. For the mid-tower and side towers, the bending modes such as No. 1, 2, 4 and 5 modes, are all excited by the in-phase vibration of two cables, while the torsional modes, No. 3, 6, 7 are induced by the out-of-phase vibration of two cables.

The deck-dominated longitudinal swing modes are listed in Table 4. It is clearly that it is the bend of mid-tower and the small amplitude of longitudinal sway of main span cables excites these modes while the side span cables contribute nothing. The lateral oscillation and rotary oscillation of deck units usually appear in the cable-dominated modes as the No. 1 and 5 shown in Table 2.

Table 3Tower-dominated modes after 10 % deck erection

No.	Frequencies (Hz)	In-plane mode shapes	Remarks
1	0.1435		1st side towers-bending mode (out-of-phase)
2	0.1934		2nd side towers-bending mode (out-of-phase)
3	0.2652		1st side towers-torsion mode (out-of-phase)
4	0.2837		3rd side towers-bending mode (out-of-phase)
5	0.2957		1st mid-tower-bending mode
6	0.3090		2nd side towers-torsion mode (out-of-phase)
7	0.3395		1st mid-tower-torsion mode

Table 4Deck-dominated modes after 10 % deck erection

No.	Frequencies (Hz)	Deck-dominated mode shapes	Remarks
1	0.1750		1st deck-dominated longitudinal mode (in phase)
2	0.2100		2nd deck-dominated longitudinal mode (out-of-phase)
3	0.2221		3rd deck-dominated longitudinal mode (in-phase)

3.3. Global modes of vibration

The global in-plane vibration modes in low order of tower-cable-deck system of twin span suspension bridge are bending and torsional modes as listed the Table 5. All the modes contain the bend and torsion modes of towers with either in-phase or out-of-phase modes of main cables following with the lifting and torsional modes of decks. However, compared with local cable-dominated modes of vibration, such as the modes of No. 3 and 5, the amplitudes of some modal motion are much smaller. As the distribution characteristics of natural frequencies shown, the global out-of-plane vibration modes only appear in the high order modes and usually include the lateral oscillation of three towers, the multi-wave sway of main cables and the rotary oscillation of deck units.

Table 5Global in-plane vibration modes after 10 % deck erection

No.	Frequencies (Hz)	Global in-plane mode shapes	Remarks
1	0.1057		1st global bending mode (in-phase)
2	0.1729		2nd global bending mode (in-phase)
3	0.2239		3rd global bending mode (in-phase)
4	0.2269		1st global torsion mode (in-phase)
5	0.2977		2nd global torsion mode (in-phase)

4.1. Variation analysis of frequencies

It is interesting to find that the natural frequencies of cable-dominated sway modes of vibration present in pairs as shown in Table 6. Before the erection of the first girder segment, in the 0 % column, the first two frequencies of cable-dominated and pure cable sway modes are almost the same as 0.0524 Hz. However, with more segments being erected, the frequencies of coupled system generate a larger difference, in which the first four frequencies of cable-dominated sway modes just slightly fluctuate but the first four frequencies of pure cable sway modes, affected more strongly from deck units, appear increasing with the erection progress.

In the vertical direction, the frequencies of cable-dominated modes also present in pairs. Following the procedure of erection, the first four frequencies of cable-dominated deck lifting modes only slightly change but the first four frequencies of cable-dominated deck torsional modes affected by deck units rises significantly. As for the tower-dominated modes of local vibration and the modes of global vibration of system, the frequencies fluctuate but slightly. It is indicated that those modes is little affected by the effect of erection of deck units. It is interesting that the frequencies of deck-dominated longitudinal modes present even decreasing tendency in the erection procedure.

The aerodynamic stability of suspension bridge usually requests that the frequency ratio of the torsional mode to the corresponding vertical mode of the bridge girder above 2.0. From Table 6, it can be seen that the first frequency ratio of the torsional mode to the lift mode is only from 1.06 for 5 % erection progress to 2.46 for 40 % erection progress. The first frequency ratio for 30 % progress is 2.01 just satisfied the desire.

The third torsional to lift frequency ratio increases from 0.75 for 5 % erection progress to 1.19 for 40 % erection progress which are all below the ratio of 2.0 clearly. The first frequency ratio of completed Ma'anshan Bridge is 2.43 calculated from its first vertical frequency of 0.099 Hz and first torsional frequency of 0.241 Hz. By comparison, it can be seen that the aerodynamic instability of stiffening girder is more likely to occur in early girder erected stage rather than completed stage for TTTS suspension bridge also. As Table 6 shows, the vertical frequencies do not vary much during and after construction, because the girder’s vertical stiffness is derived predominantly from the cable system. However, in contrast, a large percentage of the torsional stiffness comes from the girder itself. The torsional stiffness of girder is increasing with girder units erected progress as Fig. 5 shows. Therefore, the frequency ratio of torsional and lift mode is also gradually increasing.

4.2. Modal crossover phenomenon

From the foregoing study, it is known that the natural frequency of cable-dominated deck torsional modes is rising dramatically with the increasing number of stiffening deck units erected but the other modes do not as shown in Figs. 5 and 6. From Fig. 5, it is seen that the fist frequencies of cable-dominated deck lift modes and global bending modes do not vary much but the first natural frequency of cable-dominated deck torsional modes presents linear increase. As a result, a modal crossover phenomenon occur at about 5 % erection stage.

Fig. 5Comparison of first frequencies

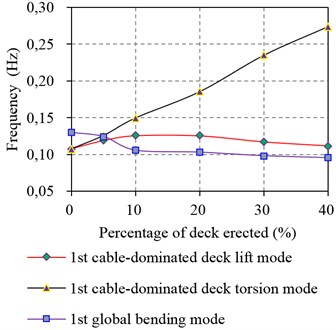
Fig. 6Comparison of high order frequencies

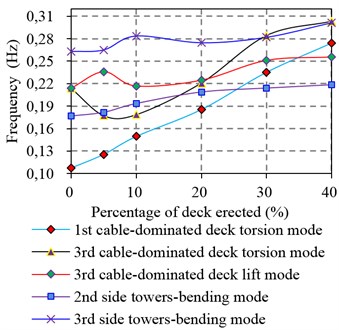
Fig. 6 shows the comparison of variation of higher mode frequencies. It is seen that the variation range of first and third frequency of torsional mode are maximum. The first torsional mode transcends the second side towers-bending mode and the third cable-dominated deck lift mode respectively at around 25 % and 35 % erected stage. Similarly, the third torsional mode frequency also transcends the others at some percentage of the erection. It is seen that the increasing deck units enhance the continuity of structure thus the torsional frequencies increase, while the vertical frequencies do not vary much during and after construction, as the girder’s vertical stiffness is derived predominantly from the cable system. The different increment of each mode frequency leads to the crossover phenomenon. This often leaves vertical and torsional frequencies dangerously close to each other during construction. Partially completed bridge girders can be extremely vulnerable to wind-induced vibrations for TTTS suspension bridge, also the evolution study of the frequency is useful reference for further measures for wind resistance.

5.1. Aerodynamic stability analysis at early erection stage

Based on the modal analysis above, the critical wind speed through the deck erection stage can be calculated by the formula:

where ${\eta }_s$ is the modified coefficient of cross section shape; ${\eta }_{\alpha }$ is the modified coefficient of wind attack angle; $\epsilon$ is the fundamental torsion to vertical bending frequency ratio; $r$ is the rotational radius of the deck cross section; ${\omega }_b$ is the angular frequency of the fundamental vertical bending mode; $b$ is the half width of the deck; $\mu$ is the density ratio of the bridge to air; ${\eta }_s$ and ${\eta }_{\alpha }$ of the bridge were taken as 0.7 and 0.8 respectively. The mass per meter of the main cable and the main girder is 4816.548 kg/m and 16430.310 kg/m respectively. The moment of inertia of the girder is 2.63×10⁶ kg∙m²/m in erection period.

The critical wind speed is 19, 23, 28, 33 m/s at 10 %, 20 %, 30 % and 40 % of deck completion, the minimum stability limit occurs at erection stages when about 10-20 % of the main span deck is in place. The worst condition still happens at the very early stage of deck erection for triple-tower suspension bridge and the instability occurs at a low wind speed. The disadvantage of low critical flutter speeds can be avoided by restricting the deck erection to a period of calm weather otherwise some measures must be taken.

5.2. Flutter control using wind ropes

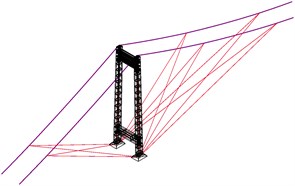
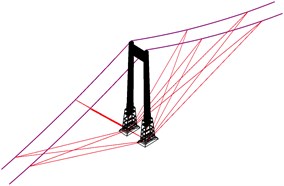
Two structural means was investigated, the provision of eccentric masses is proved not to be an efficient method. So the wind ropes method is adopted to enhance the aerodynamic stability. There are 10 groups of wind ropes with 4 ropes each, in which two are parallel and two crossover as shown in Figs. 7 and 8, at side span the ropes connect the top base of the pier and the middle points of the side main cables, while the ropes in middle span connect the 1/4 and 1/8 points of the span.

Fig. 7a) The wind ropes at the side tower and b) middle tower

a)

b)

The frequencies of cable-dominated mode are listed in Table 7 before and after the wind ropes are used, it is clear that the application of the wind ropes dramatically increases the vertical bending frequency and torsional frequency, and, the ratio of torsional frequency to vertical bending frequency. Using Eq. (1), the flutter speeds is 37,45, 53,60 m/s at 10 %, 20 %, 30 % and 40 % of deck completion, in each corresponding stage, the critical speed increases dramatically, it is clear the application of the wind ropes improve the aerodynamics ability of the structure in erection period.

Fig. 8The side view of the arrangement of wind ropes