Influence of housing ribbing modification on frequencies and shapes of vibration

1. Introduction

Because of significant costs associated with testing of real objects (toothed gears in this case), active research experiments are often substituted with simulations, that allow a complex analysis of the research assumptions. Conducting research using models allows the reduction of experimental studies to absolute minimum and is therefore justified economically [1]. In the design process of gear with lowered vibroactivity, resonance structure of excitation and resonance structure of housing calculated through modal analysis have significant meaning. The selection process of the housing design solution proposes the use of different models of discrete FEM designed individually depending on the solution of construction gear. The use of modal models allows proper selection of the gear extra cross-ribbing shape and location, including the condition of gear vibroactivity minimization, while limiting the growth of its mass.

2. FEM model of housing

Fig. 1Testing station: 1 – driving motor, 2 – driving V-belt, 3 – pulley, 4 – closing (driving) gear housing, 5 – tightening coupling, 6 – torsional shaft, 7 – flexible coupling, 8 – test (secondary) gear housing, 9 – base

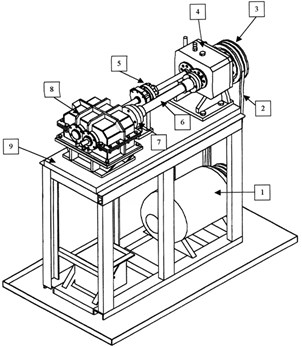
The assembled gear was mounted on a circulating power station (ref. 8 in Fig. 1), which is located in the transmission laboratory of the Transport Department of the Silesian University of Technology. The designed housings were divided in the plane of the wheels’ axes and made of welded steel S235JR plates 6 mm thick. Developed in CAD, geometric model of the housing is shown in Figure 2a. On the basis of the three-dimensional gear housing geometric models numerical models were developed. FEM models consist of approximately 29,000 solid elements. The established largest element dimension was 6 mm, which corresponds to the thickness of the housing.

Welded joints were not modeled, therefore simplifications of the housing construction were adopted in their areas. On the other hand, the models take into account threaded joints connecting the upper and the lower housing section as well as issues connected with contact between them. The developed numerical model of the housing is shown in Figure 2b.

Fig. 2Developed model of the housing: a) geometrical, b) numerical

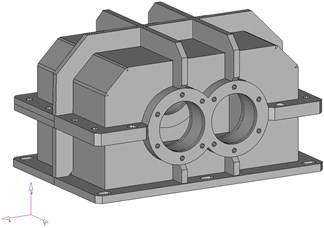
a)

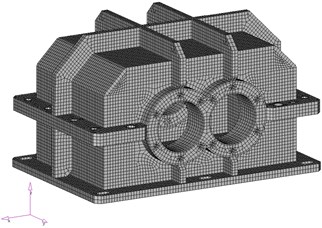
b)

3. Modal analysis of housing

In the process of FEM models identification, eigenvalue natural frequencies of the housing gear were measured using experimental modal analysis [2-4]. Table 1 presents the results of determined eigenvalue natural frequencies of the housing of the test gear and its numerical model. The presented results refer to values measured during the measurements $f_{EXP}$ and simulations $f_{FEM}$ for housing. During further analysis we compared the vibration forms of the upper gear housing and its FEM model in the resonant states. Displacement values obtained by measurements and simulations show convergence.

The compatibility of the housing FEM model and real object was also examined. The research used the MAC (Modal Assurance Criterion) coefficient determined from the formula (1), which assumes values between 0-1 (where 1 means full compatibility of FEM model and the real model) [5-6]:

where:

${\psi }_a$ – represents the analytical mode shape partitioned to the test degrees of freedom,

${\psi }_t$ – represents the test mode shapes.

Calculations carried out for the first six modal frequencies of the housing are shown in Table 2. Based on the results of the conducted experimental modal analysis, the housings numerical models were fine tuned.

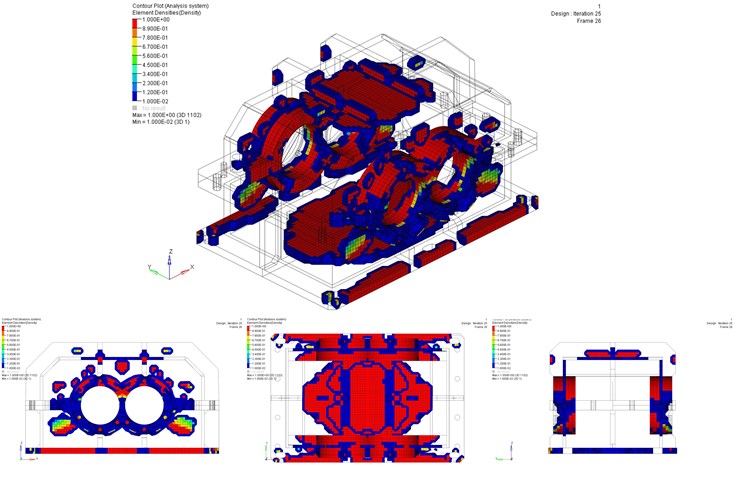
Fig. 3Housing calculation: a) areas to remove, b) areas of housing after removal

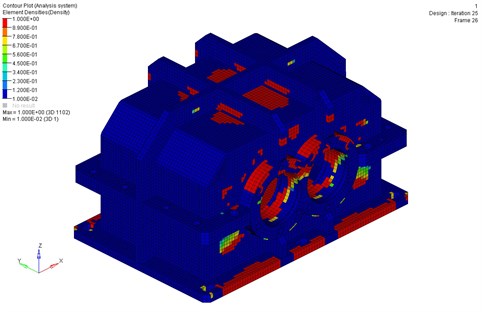
a)

b)

4. Numerical analysis of housing

The purpose of the research was the influence of housing ribbing changes on decrease of value of first natural frequency and weight of the housing. The results of the numerical calculation are that the determined areas could be removed to decrease the value of the first natural frequency. The areas which are having most impact on the value of the first natural frequency have been depicted in Fig. 3a. The picture Fig. 3b shows the housing after removing of those areas.

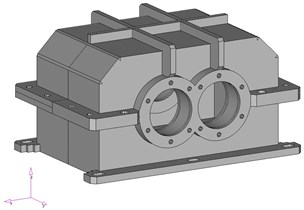
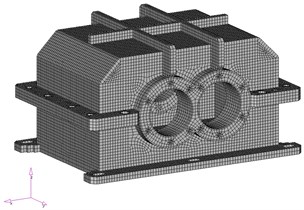
Fig. 4The modified models of gear housing: a) geometrical, b) numerical

a)

b)

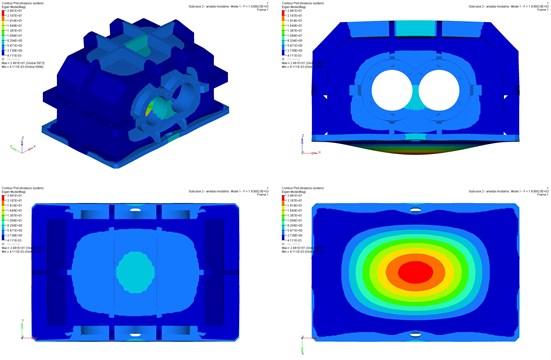
Fig. 5The first form of vibrations: a) housing before modification, b) housing after modification

a)

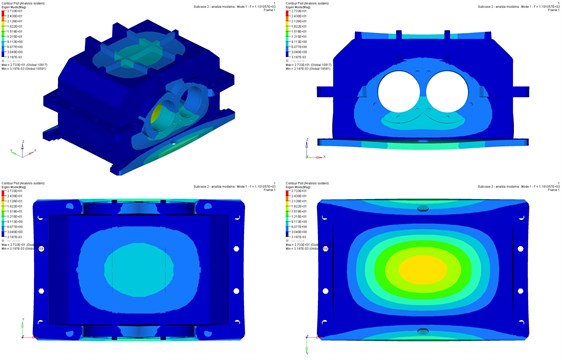
b)

Based on the analysis of modification possibilities of housing ribbing the new model of gear housing has been proposed, which is presented in Fig. 4. The new model was used for determining of the shape and frequencies of natural vibrations. The obtained results have been compared to the results before the modification of housing (Table 3).

As the result of housing modification the decrease of the value of the first natural frequency has been obtained. The decrease level was ca. 335 Hz. The housing weight was decreased ca. 7 %. The values of the next frequencies of natural vibrations have been decreased as well. The results have been depicted in Table 3.

The Figure 5 presents shapes of the first natural vibration for the housing before and after modification.

5. Conclusions

The presented experimental and theoretical modal analysis of selected structural solutions of housings gear was carried out. Results enabled to determine a rate of FEM modal parameters conformity with parameters of actual objects by determination of MAC ratio value. The obtained conformity of the results of experimental and theoretical modal analysis of examined housings solutions enabled to ascertain the correctness of prepared FEM models. The executed modal analysis of various housing versions enabled to estimate the influence of made ribbing modifications on form and frequency of its own vibrations.